-
1、 已知函数y= kx+b,当x=0时,y=8;当x=-2时,y=0,则y关于x的函数表达式为( )A、y=-2x+8 B、y=4x+8 C、y=-4x+8 D、y=2x+8
-
2、 已知函数y= kx+10,当x=3时,y=16,则y关于x的函数表达式为( )A、y=2x+10 B、y=3x+16 C、y=3x+10 D、y=16x+10
-
3、 一段导线在0℃时的电阻为2Ω,温度每增加1℃,电阻值增加0.008Ω,则这段导线的电阻R(Ω)关于温度T(℃)的函数表达式为.
-
4、 把一个长为5,宽为2的长方形的长减少x(0≤x<5),宽不变,所得长方形的面积y关于x的函数表达式为.
-
5、 在函数y= kx+2中,当x=1时,y=3;则y=0时,x=( )A、-2 B、2 C、0 D、±2
-
6、如图,已知OA是⊙O的半径,过OA上一点D作弦BE垂直于OA , 连结AB , AE . 线段BC为⊙O的直径,连接AC交BE于点F .
 (1)、求证:∠ABE=∠AEB;(2)、求证:∠ABE=∠C;(3)、若AC平分∠OAE , 请解决以下四个问题
(1)、求证:∠ABE=∠AEB;(2)、求证:∠ABE=∠C;(3)、若AC平分∠OAE , 请解决以下四个问题①求证:AE∥BC .
②求证: .
③求∠ABE的度数.
④求的值.
-
7、已知抛物线y=ax2+bx+6与的一个交点为A(4,0),且过点B(-1,5).
 (1)、求该二次函数的解析式;(2)、将该二次函数的图象向左平移m(m>0)个单位,若抛物线再次经过点B时,求m的值;(3)、点C(n , n)与点均在该函数图象上,且这两点关于函数图象的对称轴对称,求n的值及点D的坐标.
(1)、求该二次函数的解析式;(2)、将该二次函数的图象向左平移m(m>0)个单位,若抛物线再次经过点B时,求m的值;(3)、点C(n , n)与点均在该函数图象上,且这两点关于函数图象的对称轴对称,求n的值及点D的坐标. -
8、如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
 (1)、画出△ABC绕点C顺时针旋转90°后的△A1B1C1 .(2)、求线段长度.(3)、求点A旋转到点A1所经过的路径长.
(1)、画出△ABC绕点C顺时针旋转90°后的△A1B1C1 .(2)、求线段长度.(3)、求点A旋转到点A1所经过的路径长. -
9、在一个箱子中放有三张完全相同的卡片,卡片上分别标有数学1、2、3.(1)、从箱子中任意取出一张卡片,求抽到标有数字1的卡片的概率;(2)、从箱子中任意取出两张卡片,求两张卡片上的数字和是2的倍数的概率,用列表法或画树状图的方法加以说明.
-
10、已知抛物线y=-x2+bx+4过点 (1,5).(1)、求b的值.(2)、判断P(2,4)是否在该函数图象上,并说明理由.
-
11、如图,△ABC内接于⊙O , A为劣弧BC的中点,∠BAC=120°,BD为⊙O的直径,连结AD , 若AD= , 则AC的长为 .

-
12、已知A(-2,y1),B(-1,y2),C(4,y3)三点都在二次函数y=a(x-2)2+1(a>0)的图象上,则y1 , y2 , y3的大小关系为 .
-
13、一条排水管的截面如图所示,已知排水管的半径OA=5 dm,水面宽AB=6 dm,某天下雨后,水面宽度变为8 dm(水面仍在圆心O下面),则此时排水管水面上升了dm.

-
14、已知线段a=2,b=8,则a , b的比例中项线段是 .
-
15、 设二次函数y=a(x-m)(x-m-2)(a , m是常数,a≠0),则下列说法正确的是( )A、当a=1时,函数y的最小值为2 B、当a=-1时,函数y的最大值为2 C、当a=2时,函数y的最小值为-2 D、当a=-2时,函数y的最大值为-2
-
16、如图,在三角形ABC中, , , 将此三角形绕点沿顺时针方向旋转后得到三角形 , 若点恰好落在线段上,、交于点 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、对于抛物线 ,下列说法错误的是( )A、对称轴是直线 B、函数的最大值是3 C、开口向下,顶点坐标(5,3) D、当时,随的增大而增大.
-
18、关于抛物线y=x2+bx-1与x轴的交点有( )A、0个 B、1个 C、2个 D、3个
-
19、小磊和小轩在课外练习中碰到了一个问题,需要对多项式进行因式分解.小磊认为该整式一定有一个因式 , 小轩认为必有因式是 , 两人找到老师寻求帮助.老师提供了一个方法:因式分解是整式乘法的逆运算.若整式A能被整式B整除,则B必为A的一个因式.老师给出了演算方法:
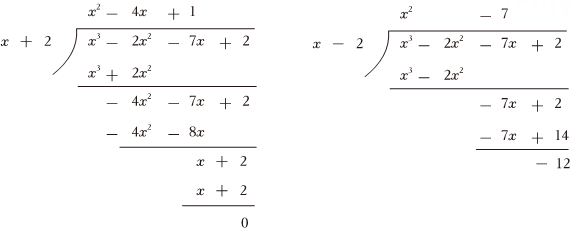 (1)、观察老师的演算后,你认为同学的想法是对的;(2)、已知多项式的其中一个因式为 , 请试着根据老师的方法列出演算过程,并将多项式进行因式分解;(3)、若多项式能因式分解成与另一个完全平方式,求与的值.
(1)、观察老师的演算后,你认为同学的想法是对的;(2)、已知多项式的其中一个因式为 , 请试着根据老师的方法列出演算过程,并将多项式进行因式分解;(3)、若多项式能因式分解成与另一个完全平方式,求与的值. -
20、临近期末,班级想给优秀的学生准备奖品,奖品分为甲套餐与乙套餐,已知购买个甲套餐比购买个乙套装少用元,用元购买甲套餐和用元购买乙套餐的个数相同.(1)、求这两种套餐的单价分别为多少元;(2)、班级计划用元经费购进甲套餐与乙套餐两种奖品,要求每种套餐至少购进种且刚好用完经费,请你设计进货方案.