-
1、如图,一根竹竿AB斜靠在竖直的墙上,P是AB的中点,在竹竿的顶端沿墙面滑下的过程中,OP长度的变化情况是( )
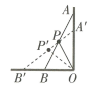 A、不断增大 B、不断减小 C、先减小后增大 D、不变
A、不断增大 B、不断减小 C、先减小后增大 D、不变 -
2、 如图,中, , 于点D, , , 则.
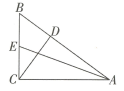
-
3、在△ABC 中,∠C=90°, , 则=.
-
4、如图, Rt △ABC 中,∠ACB=90°,CD⊥AB于点D,则下列结论不一定成立的是( )
 A、∠1+∠2=90° B、∠2=∠3 C、∠1=∠4 D、∠1=30°
A、∠1+∠2=90° B、∠2=∠3 C、∠1=∠4 D、∠1=30° -
5、如图所示,在长方形ABCD中,已知AB=6,AD=4,在长方形ABCD外画△ABE,使AE=BE=5,请建立适当的平面直角坐标系,并求出各顶点的坐标.

-
6、如图,方格纸中每个小方格都是边长为1个单位的正方形,学校的坐标为A(2,1),图书馆的坐标为 B(-1,-2),解答下列问题:

⑴在图中建立平面直角坐标系,并标出坐标原点O;
⑵若体育馆的坐标为C(1,3),请在坐标系中标出体育馆的位置C;
⑶顺次连结学校、图书馆、体育馆所在的点,得到△ABC,求△ABC的面积.
-
7、五子棋是一种两人对弈的棋类游戏,规则如下:在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,首先在任一方向(横向、竖向或者是斜着的方向)上连成五子连珠者为胜.如图是两个五子棋爱好者的对弈图.在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),为了不让白方在短时间内获胜,此时黑方应该下在坐标为的位置处.

-
8、已知等边△ABC 的边长为2,以BC的中点为原点,BC 所在的直线为x轴,则点A 的坐标为.
-
9、四边形 ABCD 的形状和尺寸如图所示.若按下列选项建立平面直角坐标系,则其中点C的坐标为(2.5,1.5)的是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
10、有甲、乙、丙三人,他们所在的位置不同,且三人都以相同的单位长度,以正东、正北为x轴和y轴的正方向建立原点不同的坐标系,甲说:“以我为坐标原点,乙的位置是(4,3).”丙说:“以我为坐标原点,乙的位置是(-3,-4).”那么如果以乙为坐标原点,甲和丙的位置分别是( )A、(3,4),(-3,-4) B、(4,-3),(3,-4) C、(-3,-4),(4,3) D、(-4,-3),(3,4)
-
11、 2025 年 2 月 17新素材日,《哪吒之魔童闹海》成为中国首部进入全球影史票房榜前十的电影.如图是某影院部分座位平面示意图,若座位A 的坐标为(3,2),座位B 的坐标为(-1,1),则座位C的坐标为( )
 A、(1,4) B、(4,1) C、(0,3) D、(3,0)
A、(1,4) B、(4,1) C、(0,3) D、(3,0) -
12、在平面直角坐标系中,已知点 A 的坐标为(4,3).
 (1)、如图,若△ABC 是关于直线y=1 对称的轴对称图形,求点 B 的坐标;(2)、若△ABC 是关于直线y=a(a≤3)对称的轴对称图形,求点 B 的坐标.(用含 a 的式子表示)
(1)、如图,若△ABC 是关于直线y=1 对称的轴对称图形,求点 B 的坐标;(2)、若△ABC 是关于直线y=a(a≤3)对称的轴对称图形,求点 B 的坐标.(用含 a 的式子表示) -
13、如图,直角坐标系中两点 A,B的坐标分别为A(0, ),B(-1,0),点 P为线段OB上一动点,P关于AB,AO 的对称点分别为点 C,D,连结CD,分别交 AB,AO 于点 M,N,则 CD 的最大值是 , ∠MPN的度数是.

-
14、已知第一象限内有一点 P(2,3),点 P 关于x轴的对称点为 P1 , P1关于y轴的对称点为 P2 , P2关于x轴的对称点为P3 , 按此规律,依次得到 P4 , P5 , P6 , …,则点P2025的坐标为( )A、(2,3) B、(2,-3) C、(-2,-3) D、(-2,3)
-
15、若点A(a,4)在第二象限,则点 A 关于直线m(直线 m上各点的横坐标都是2)对称的点的坐标是 ( )A、(-a,4) B、(4-a,4) C、(-a-4,-4) D、(-a-2,-4)
-
16、如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(-3,4),B(-3,1),C(1,-2).
 (1)、请分别画出△ABC 的边AC上的中线BE 和边AB上的高 CF,并直接写出点 E,F 的坐标为E(▲),F(▲).(2)、画出与△ABC 关于直线 AB 对称的图形△ABD,并写出点D 的坐标.
(1)、请分别画出△ABC 的边AC上的中线BE 和边AB上的高 CF,并直接写出点 E,F 的坐标为E(▲),F(▲).(2)、画出与△ABC 关于直线 AB 对称的图形△ABD,并写出点D 的坐标. -
17、将平面直角坐标系中△ABC 的三个顶点的纵坐标乘-1,横坐标不变,则所得的三角形与原三角形关于轴对称.
-
18、如图,小琪和小亮下棋,小琪执圆形棋子,小亮执方形棋子,若棋盘中心的圆形棋子的位置用(-1,1)表示,小亮将第4枚方形棋子放入棋盘后,所有棋子构成轴对称图形,则小亮放方形棋子的位置可能是( )
 A、(-1,-1) B、(-1,3) C、(0,2) D、(-1,2)
A、(-1,-1) B、(-1,3) C、(0,2) D、(-1,2) -
19、如果点 P(2,b)和点Q(a,-3)关于直线x=1对称,则a+b的值是
-
20、若点P(x,-4)与点Q(3,y)关于原点对称,则x-y等于.