-
1、如图,若 , , , , 试说明 .

-
2、已知平面上的三个点、、和直线 , 根据要求画图.
 (1)、画射线;(2)、确定点的位置,使得点既在直线上,又在直线上;(3)、在直线上确定点的位置,使得点到点与点的距离之和最小.
(1)、画射线;(2)、确定点的位置,使得点既在直线上,又在直线上;(3)、在直线上确定点的位置,使得点到点与点的距离之和最小. -
3、填空并在括号内加注理由.
已知:如图, , , , , 求证: .

证明:∵ , (已知)
∴()
∴()
∴()
∵(已知)
∴()
∴(同位角相等,两直线平行)
∴()
∵(已知)
∴
∴
∴()
-
4、钟面上的数学
基本概念:钟面角是指时钟的时针与分针所成的角.如图1,即为某一时刻的钟面角,通常

[简单认识]时针和分针在绕点O一直沿着顺时针方向旋转,时针每小时转动的角度是 , 分针每小时转动一周,角度为 . 由此可知:
(1)、时针每分钟转动°,分针每分钟转动°:(2)、[初步研究]已知某一时刻的钟面角的度数为 , 在空格中写出一个与之对应的时刻:
①当时,;
②当时,;
(3)、如图2,钟面显示的时间是8点04分,此时钟面角 .(4)、[深入思考]在某一天的下午2点到3点之间(不包括2点整和3点整).
①时针恰好与分针重叠,则这一时刻是 ;时针恰好与分针垂直,求此时对应的时刻是 ;
②记钟面上刻度为3的点为C , 当钟面角的两条边所在射线与射线中恰有一条是另两条射线所成角的角平分线时,请直接写出此时对应的时刻.
-
5、已知、 , 求作: , 使(保留作图痕迹).

-
6、计算:
⑴;
⑵;
⑶;
⑷ .
-
7、如图,能用字母表示的以点C为端点的线段的条数为m , 能用字母表示的以点C为端点的射线的条数为n , 则的值为 .

-
8、在同一平面内,若 , 则与的位置关系是 .
-
9、如图所示,和是直线 , 被直线所截形成的同位角;的内错角有 .

-
10、如图,已知 , 过点画 , 画的平分线 , 、交于点 , 量一量的度数,约为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、图中直线的表示方法,不正确的有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
12、若互不重合的三条直线 , , 之间满足: , 则与之间的位置关系为( )A、与平行 B、与垂直 C、与相交 D、以上都有可能
-
13、如果从某个多边形的一个顶点出发,可以作2条对角线,则这个多边形的边数是( )A、4 B、5 C、6 D、7
-
14、如图,平分 , 平分 , , , 则的度数为( )
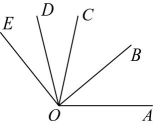 A、45° B、50° C、65° D、70°
A、45° B、50° C、65° D、70° -
15、下列直线、射线、线段中,能相交的是( )A、
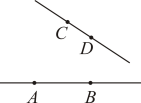 B、
B、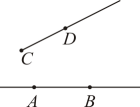 C、
C、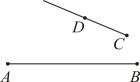 D、
D、
-
16、如图(1),已知△ABC为直角三角形,∠BCA=90°,在 BC 的延长线上取一点D,使得 点 E 是AB 的中点,连结DE,M为ED的中点,连结CM,AD.
 (1)、试判断 CM 与 ED 的位置关系,并说明理由.(2)、若∠AED=105°,请求出∠BAC 的度数.(3)、如果将题中“在BC的延长线上取一点D”改为“在CB 的延长线上取一点 D”,其余条件不变,如图(2)所示.若∠AED=165°,请求出∠BAC 的度数.
(1)、试判断 CM 与 ED 的位置关系,并说明理由.(2)、若∠AED=105°,请求出∠BAC 的度数.(3)、如果将题中“在BC的延长线上取一点D”改为“在CB 的延长线上取一点 D”,其余条件不变,如图(2)所示.若∠AED=165°,请求出∠BAC 的度数. -
17、一辆装满货物的卡车,高2.5m,宽1.6m,要开进上边是半圆,下边是长方形的隧道,如图所示,已知半圆的直径为2m ,长方形的另一条边长是2.3m .(1)、此卡车能否通过隧道?试说明你的理由.(2)、为了适应车流量的增加,想把隧道改为双行道,要使宽为1.2m,高为2.8 m的卡车能安全通过,那么此隧道的宽至少增加到多少?
-
18、如图,△ABC 中,∠ABC=90°,AC=20,BC=12.
 (1)、直接写出AB 的长度为.(2)、设点 P 在AB上,若∠PAC=∠PCA,求AP的长.(3)、设点 M 在 AC 上,若△MBC 为等腰三角形,直接写出AM 的长.
(1)、直接写出AB 的长度为.(2)、设点 P 在AB上,若∠PAC=∠PCA,求AP的长.(3)、设点 M 在 AC 上,若△MBC 为等腰三角形,直接写出AM 的长. -
19、在平面内,分别用相同的3根,5根,6根,…火柴首尾顺次相接,能搭成什么形状的三角形呢?通过尝试,列表如下:
火柴根数
3
5
6
…
示意图
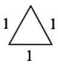

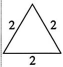
…
形状
等边三角形等腰三角形等边三角形
根据以上信息,解答下列问题:
(1)、4根火柴能搭成三角形吗?(2)、12 根火柴能搭成几种不同形状的三角形?请画出它们的示意图. -
20、如图,在长方形 ABCD 中,△AEF 为等腰直角三角形,且∠AEF=90°,点E 在线段 BC 上,点 F 在线段CD 上,若 3(AB+BE)= 2(AD+DF),则.
