相关试卷

1、如图，自行车的车架上常常会焊接一横梁，运用的数学原理是（）

A、两点之间，线段最短 B、三角形具有稳定性 C、三角形两边之和大于第三边 D、垂线段最短

查看解析
2、先化简，再求值： $2 m - m (m - 2) + (m + 3) (m - 3)$ ，其中 $m = 2$ ．

查看解析
3、计算： $|1 - \sqrt{3}| - 2 \sin 60 ° + {(\frac{1}{4})}^{- 1} - {(2025 - π)}^{0}$ ．

查看解析
4、如图， $△ A O B$ 和 $△ A C D$ 均为正三角形，且顶点 $B$ 、 $D$ 均在双曲线 $y = \frac{6}{x} (x > 0)$ 上，连接 $B C$ 交 $A D$ 于 $P$ ，连接 $O P$ ，则图中 $S_{△ O B P} =$ ．

查看解析
5、如图， $△ A B C$ 与 $△ D E F$ 是以点O为位似中心的位似图形，其位似比为 $3 : 2$ ，则 $△ A B C$ 与 $△ D E F$ 的面积比是．

查看解析
6、圆锥的底面圆的半径为10，圆锥母线长为20，则圆锥侧面展开图的面积为．

查看解析
7、如图，点A，B，C，D在同一条直线上，点E，F分别在直线 $A B$ 的两侧，且 $A E = B F$ ， $∠ A = ∠ B$ ， $∠ D C E = ∠ C D F$ ，若 $A B = 16$ ， $A C = 4$ ，则 $C D$ 的长为（）

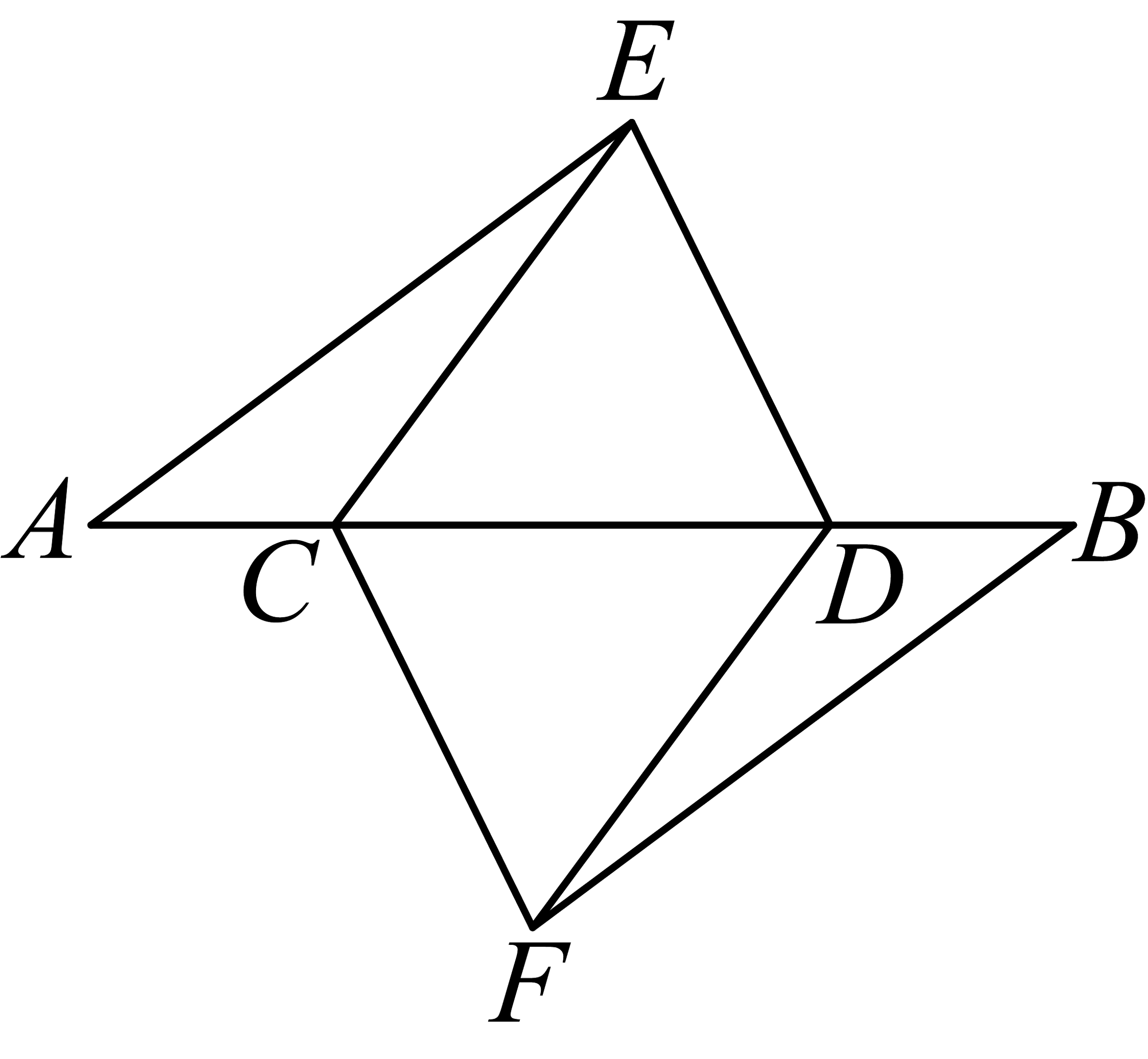A、4 B、6 C、8 D、10

查看解析
8、打水漂源自民间传统游戏，又名轻功水上漂，七点漂，漂瓦．它能够锻炼玩家的手眼协调能力和投掷技巧．长沙少年小明连续打水漂8次的成绩如表所示：
次数
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
成绩/下
8
9
8
8
7
9
16
8
则小明连续打水漂8次成绩的众数和中位数分别是（）

A、8，8 B、8，8.5 C、9，8 D、8，9

查看解析
9、如图1，在矩形 $A B C D$ 中， $A B = 4$ ， $B C = 3$ ，点E在边 $B C$ 上运动（不与点B和点C重合），将 $A E$ 绕点A顺时针旋转得到 $A F$ ，旋转角等于 $∠ B A C$ ，连接 $C F$ ，过点F作 $F M ⊥ A C$ 于点M．

(1)、求证： $△ A B E ≌ △ A M F$ ．

(2)、当直线 $F M$ 恰好经过点E时，求 $C F$ 的长．

(3)、如图2，连接 $D F$ ，试探究 $D F$ 是否存在最小值．若存在，请求出这个最小值；若不存在，请说明理由．

查看解析
10、如图，在 $△ A B C$ 中， $A C = B C$ ， D是 $B C$ 上的一点，且满足 $∠ B A D = \frac{1}{2} ∠ C$ ，以 $A D$ 为直径的 $⊙ O$ 分别与 $A B, A C$ 相交于点E，F．

(1)、求证：直线 $B C$ 是 $⊙ O$ 的切线．

(2)、连接 $E F$ ，若 $\tan ∠ A E F = \frac{4}{3}$ ， $A D = 4$ ，求 $B D$ 的长．

查看解析
11、随着科技的发展，人工智能渐渐走进了人们的生活，现从甲、乙两款人工智能软件调查得分中分别随机抽取了 $20$ 名用户的得分（得分用x表示）数据进行整理、描述和分析，共分为四组：A． $60 < x \leq 70$ ， B． $70 < x \leq 80$ ， C． $80 < x \leq 90$ ， D． $90 < x \leq 100$ ．下面给出了部分信息．
甲款人工智能软件得分数据：
$64$ ， $70$ ， $75$ ， $76$ ， $78$ ， $78$ ， $85$ ， $85$ ， $85$ ， $85$ ， $86$ ， $89$ ， $90$ ， $90$ ， $94$ ， $95$ ， $98$ ， $98$ ， $99$ ， $100$ ．
乙款人工智能软件在C组内（ $80 < x \leq 90$ ）的所有得分数据：
$85$ ， $86$ ， $87$ ， $88$ ， $88$ ， $88$ ， $90$ ， $90$ ．
甲、乙两款人工智能软件得分统计表：
软件
平均数
中位数
众数
方差
甲
$86$
$85.5$
b
$96.6$
乙
$86$
a
$88$
$69.8$
根据以上信息，解答下列问题：

(1)、填空： $a =$ ________， $b =$ ________， $m =$ ________．

(2)、根据以上数据，你认为哪款人工智能软件更受用户欢迎？请说明理由（写出一条理由即可）．

(3)、若本次调查有 $1200$ 名用户对甲款人工智能软件进行了调查评分，有 $900$ 名用户对乙款人工智能软件进行了评分，估计这次调查对甲、乙两款人工智能软件非常满意（ $90 < x \leq 100$ ）的总用户数．

查看解析

12、1672年，丹麦数学家莫尔在他的著作《欧几里得作图》中指出：只用圆规可以完成一切尺规作图.1797年，意大利数学家马斯凯罗尼又独立发现此结论，并写在他的著作《圆规的几何学》中．请你利用数学家们发现的结论，完成下面的作图题：

如图，已知 $⊙ O$ ，请你用直尺和圆规作圆的内接正方形．（按如下步骤完成，保留作图痕迹）

作法

图形

①作直径 $A C$ ；

②过点A作 $A C$ 的垂线 $A M$ ；

③作 $∠ M A C$ 的平分线交 $⊙ O$ 于点B；

④以点A为圆心， $A B$ 的长为半径作弧，交 $⊙ O$ 于点D；

⑤依次连接 $B C ， C D ， D A$ ，四边形 $A B C D$ 就是所求作的正方形

查看解析

13、解不等式组 $\{\begin{array}{l} 5 x + 2 > 3 x - 2 ① \\ \frac{1 - x}{2} \geq 1 ② \end{array}$ ．

查看解析
14、化简： $(1 - \frac{x}{x + 2}) \cdot \frac{x^{2} + 4 x + 4}{x^{2} - 4}$ ．

查看解析
15、计算： $\sqrt{8} - \frac{\sqrt{2}}{3} \times \sqrt{9}$ ．

查看解析
16、如图1，这是小区围墙上的花窗，其形状是扇形的一部分，图2是其几何示意图（阴影部分为花窗）．通过测量，得到扇形 $A O B$ 的圆心角的度数为 $90 °$ ， $O A = 4 m$ ， C，D分别为 $O A, O B$ 的中点，则花窗的面积为 $m^{2}$ ．（结果保留 $π$ ）

查看解析
17、如图1，风铃，又称铁马，古称“铎”，常见于中国传统建筑屋檐下，六角形风铃的平面示意图如图2所示，其底部可抽象为正六边形 $A B C D E F$ ，连接 $C F$ ，则 $∠ A F C$ 的度数为．

查看解析
18、一次函数 $y = k x + 1$ 的函数值y随x的增大而减小，则它的图象不经过第象限．

查看解析
19、进位制是人们为了记数和运算方便而约定的记数系统，约定逢十进一就是十进制，逢二进一就是二进制，“逢几进一”就是几进制．各进制表示的数也可以转化，如：十进制数5用二进制可以表示为101，即 $5 = 1 \times 2^{2} + 0 \times 2^{1} + 1 \times 2^{0}$ ，则二进制数110010表示的十进制数为（）

A、3 B、50 C、100 D、25

查看解析
20、“共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务，成为城市交通出行的新方式．小张对他所在小区居民当月使用“共享单车”的次数进行了抽样调查，并绘制成了如图所示的频数分布直方图（每一组含前一个边界值，不含后一个边界值），则下列说法错误的是（）

A、小张一共抽样调查了74人 B、样本中当月使用“共享单车”30次 $~ 40$ 次的人数最多 C、样本中当月使用“共享单车”不足20次的有12人 D、样本中当月使用“共享单车”不少于40次的人数不到总人数的 $\frac{1}{3}$

查看解析

上一页 609 610 611 612 613 下一页跳转

次数	第1次	第2次	第3次	第4次	第5次	第6次	第7次	第8次
成绩/下	8	9	8	8	7	9	16	8

软件	平均数	中位数	众数	方差
甲	$86$	$85.5$	b	$96.6$
乙	$86$	a	$88$	$69.8$