相关试卷

1、直线 $y = 2 x$ 与直线 $y = - x + 5$ 的交点坐标为（）

A、(5， 10) B、( $\frac{5}{3}$ ， $\frac{10}{3}$ ) C、(4， 8) D、( $\frac{4}{3}$ ， $\frac{7}{3}$ )

查看解析
2、下列由左边到右边的变形，属于因式分解的是（）

A、 $(a + 1) (a - 1) = a^{2} - 1$ B、 $a^{2} + a + 1 = a (a + 1) + 1$ C、 $a m + b m = m (a + b)$ D、 $a^{2} + 2 a = a^{2} (1 + \frac{2}{a})$

查看解析
3、 2024年10月30日，“神舟十九号”载人飞船发射取得圆满成功. 在发射过程中，“神舟十九号”载人飞船飞行速度约为484000米/分，数据“484000”用科学记数法表示为（）

A、 $4.84 \times 1 0^{5}$ B、 $4.84 \times 1 0^{6}$ C、 $48.4 \times 1 0^{4}$ D、 $0.484 \times 1 0^{6}$

查看解析
4、【问题背景】
如图1，在 $△ A B C$ 中，已知 $A B = A C$ ， $∠ B A C = 9 0^{°}$ ， AH是 $△ A B C$ 的高， $A H = 4 c m$ ， $B C = 8 c m$ ，过点C的直线 $M N ⊥ B C$ ，动点D从点C开始沿射线CB方向以3cm/s的速度运动，动点E也同时从点C开始在直线MN上以2cm/s的速度向远离C点的方向运动，连接AD、AE，设运动时间为t(t>0)秒

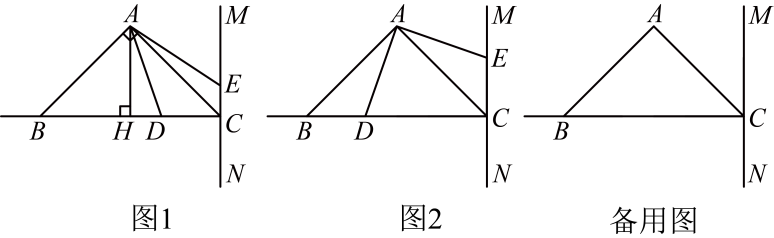(1)、【思考尝试】请直接写出CD、CE的长度（用含有t的代数式表示）：CD=cm，CE=cm

(2)、当t为多少时， $△ A B D$ 的面积为 $12 c m^{2}$ ？

(3)、【深入探究】如图2，当点D在线段BC上，且 $A D ⊥ A E$ 时， $△ A B D$ 是否与 $△ A C E$ 全等？说明理由，此时 $C D + C E$ 的值为多少？

(4)、请利用备用图探究，当点D在线段CB的延长线上，且 $A D ⊥ A E$ 时，CD与CE有什么数量关系？请说明理由.

查看解析
5、问题情境：如图1， $A B ∥ C D$ ， $∠ P A B = 13 0^{°}$ ， $∠ P C D = 12 0^{°}$ ，求 $∠ A P C$ 度数.
小明的思路是：过P作 $P E ∥ A B$ ，通过平行线性质来求 $∠ A P C$ .

(1)、按小明的思路，易求得 $∠ A P C$ 的度数为度；(直接写出答案)

(2)、问题迁移：如图2， $A B ∥ C D$ ，点P在射线OM上运动，记 $∠ P A B = α$ ， $∠ P C D = β$ ，当点P在B、D两点之间运动时，问 $∠ A P C$ 与 $α$ ， $β$ 之间有何数量关系？请说明理由；

(3)、在(2)的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出 $∠ A P C$ 与 $α$ ， $β$ 之间的数量关系.

查看解析
6、宝兰客专是首条贯通丝绸之路经济带的高铁线，宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作，人文交流具有十分重要的意义.试运行期间，一列动车从西安开往西宁，一列普通列车从西宁开往西安，西宁与西安相距1260千米，两车同时出发，两车出发后3小时相遇，设普通列车行驶的时间为x（小时），两车之间的距离为y（千米），图中的折线表示y与x之间的关系，根据图象，解答下列问题：

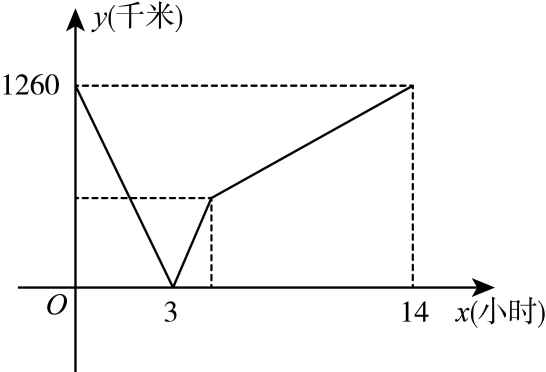(1)、普通列车到达终点共需小时，它的速度是千米/小时；

(2)、求动车的速度；

(3)、动车行驶多长时间与普通列车相距140千米？

查看解析
7、数与形是数学研究的两大部分，它们间的联系称为数形结合，整式乘法中也可以利用图形面积来论证数量关系，现用砖块相同的面（如图1，长为a，宽为b的小长方形）拼出以下图形，延长部分边框，则把这些拼图置于如图所示的正方形或大长方形内，请解答下列问题.

(1)、图2中空白面积为 $S_{1}$ ，根据图形中的数量关系，用含a，b的式子表示 $S_{1}$ .

(2)、图2，图3中空白部分面积 $S_{1}$ ， $S_{2}$ 分别为19，68，求ab值.

查看解析
8、如图，点B，C，E，F在同一直线上，点A，D在BC的异侧， $A B = C D$ ， $B F = C E$ ， $∠ B = ∠ C$ .

(1)、求证： $A E ∥ D F$ .

(2)、若 $∠ A + ∠ D = 14 4^{°}$ ， $∠ C = 3 0^{°}$ ，求 $∠ A E C$ 的度数.

查看解析
9、在“五·四”青年节中，全校举办了文艺汇演活动，小丽和小芳都想当节目主持人，但现在只有一个名额，小丽想出了一个办法，她将一个转盘（均质的）均分成6份，如图所示.

游戏规定：随意转动转盘，

(1)、指针指到1的可能性是多少？

(2)、若指针指到3，则小丽去；若指针指到2，则小芳去，若你是小芳，会同意这个办法吗？为什么？

查看解析
10、如图，已知 $△ A B C$ 中，

(1)、尺规作图：作线段AB的垂直平分线DE，分别交边BC、AB于点D、E（不写作法，保留作图痕迹并标明字母）；

(2)、连接AD，若 $A B = 8$ ， $△ A B C$ 的周长是18，求 $△ A C D$ 的周长.

查看解析
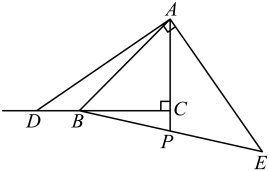
11、先化简，再求值： $[(x + 2 y)^{2} - (3 x + y) (3 x - y) - 5 y^{2}] \div (- \frac{1}{2} x)$ ，其中， $(x - 1)^{2} + | 2 y + 1 | = 0$

查看解析
12、如图所示，在 $R t △ A B C$ 中， $A C = B C$ ， $∠ A C B = 9 0^{°}$ ，点D为射线CB上的动点， $A E = A D$ ，且 $A E ⊥ A D$ ， BE与AC所在的直线交于点P，若 $\frac{A C}{P C} = \frac{8}{3}$ ，则 $\frac{B D}{C D}$ =.

查看解析
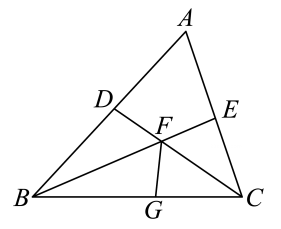
13、如图，在锐角三角形ABC中， $∠ B A C = 6 0^{°}$ ， BE，CD分别为 $△ A B C$ 的角平分线BE，CD相交于点F，FG平分 $∠ B F C$ ，已知 $B D = 3$ ， $C E = 2$ . $△ B F C$ 的面积为2.5， $△ B C D$ 的面积为.

查看解析
14、若 $a + \frac{1}{a} = 2$ ，则 $a^{2} + \frac{1}{a^{2}}$ 的值是.

查看解析
15、一根弹簧原长13厘米，挂物体质量不得超过16千克，并且每挂1千克就伸长0.8厘米，弹簧长度y(厘米)与所挂物体质量x(千克)的关系为 ( $0 \leq x \leq 16$ ).

查看解析
16、若等腰三角形的周长为13，一边长为3，则其腰长是.

查看解析
17、如图所示，在 $△ A B C$ 中， $∠ A B C = 6 8^{°}$ ， BD平分 $∠ A B C$ ， P为线段BD上一动点，Q为边AB上一动点，当 $A P + P Q$ 的值最小时， $∠ A P B$ 的度数是（）

A、 $11 8^{°}$ B、 $12 5^{°}$ C、 $13 6^{°}$ D、 $12 4^{°}$

查看解析
18、自定义运算： $a * b = {\begin{array}{l} a - 2 b (a < b) \\ 2 a - b (a \geq b) \end{array}$ ，例如： $2 ⋆ (- 4) = 2 \times 2 - (- 4) = 8$ ，若 m，n 在数轴上的位置如图所示，且 $(m + n) ⋆ (m - n) = 7$ ，则 $6 n - 2 m + 2021$ 的值等于（）

A、2028 B、2035 C、2028 或 2035 D、2021 或 2014

查看解析
19、将 n 个边长都为 1 的正方形按如图所示的方法摆放，点 $A_{1}, A_{2}$ ， ···， $A_{n}$ 分别是正方形对角线的交点，则 2022 个正方形照这样重叠形成的重叠部分的面积和为（）

A、 $\frac{2021}{4}$ B、 $\frac{2021}{3}$ C、1 D、2020

查看解析
20、在 $△ A B C$ 中， $A C = 6$ ，中线AD=7，则AB的长度不可能是( )

A、7 B、9 C、17 D、19

查看解析

上一页 583 584 585 586 587 下一页跳转