相关试卷

1、下列函数中，y随x的增大而减小的函数是（）

A、 $y = 2 x + 1$ B、 $y = x - 4$ C、 $y = 2 x$ D、 $y = - x + 1$

查看解析
2、学校举行“绿美乡村”义务植树活动，五个小组在这次活动中植树的棵数分别为10，11，9，10，12.下列关于该组数据描述正确的是( )

A、众数为10 B、平均数为10 C、方差为2 D、中位数为9

查看解析
3、在 $▱ A B C D$ 中， $A B = 3$ ， $A D = 5$ ，则 $▱ A B C D$ 的周长为（）

A、8 B、10 C、12 D、16

查看解析
4、若 $\sqrt{x - 2}$ 有意义，则 x 的取值范围是（）

A、 $x > 2$ B、 $x \geq 2$ C、 $x < 2$ D、 $x \leq 2$

查看解析
5、在 $Δ A B C$ 中，点D是线段AB上一动点，连接CD. 将线段CD绕点C逆时针旋转至CE，记旋转角为 $α$ ，连接AE. 取AE的中点为G，连接CG.

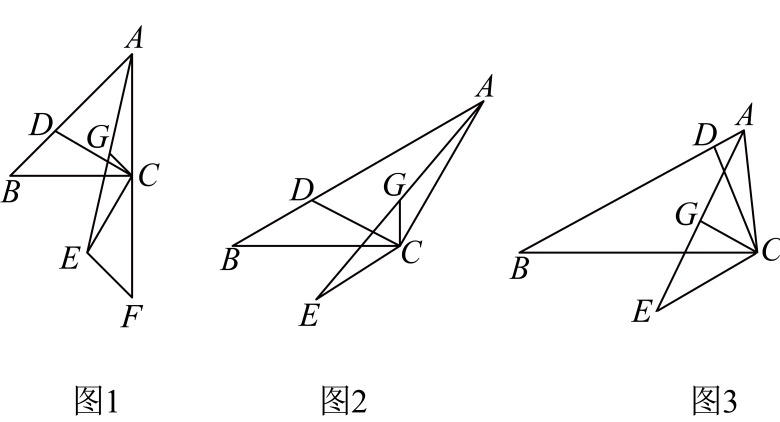(1)、【特例感知】如图1，已知 $Δ A B C$ 是等腰直角三角形， $A C = B C$ ， $∠ A C B = 9 0^{°}$ ， $α = 9 0^{°}$ . 延长AC至点F，使 $A C = C F$ ，连接EF. 请直接写出EF与BD的数量关系， CG与BD的数量关系.

(2)、【类比迁移】如图2，已知 $Δ A B C$ 是等腰三角形， $A C = B C$ ， $∠ A C B = 12 0^{°}$ ， $α = 6 0^{°}$ . 探究线段CG与BD的数量关系，并证明你的结论.

(3)、【拓展应用】如图3，已知在 $△ A B C$ 中， $B C = 13$ ， $A C = 7$ ， $∠ A B C = 3 0^{°}$ ， $∠ A C B = 18 0^{°} - α$ . 在点D的运动过程中，求线段CG长度的最小值.

查看解析
6、已知 $f (x) = a_{1} x^{n} + a_{2} x^{n - 1} + ⋯ + a_{n - 1} x^{2} + a_{n} x + c$ （其中 $a_{1}$ ， $a_{2}$ ， $⋯$ ， $a_{n}$ 是各项的系数，c 是常数项），我们规定 f(x)
的伴随多项式是g(x)，且 $g (x) = n a_{1} x^{n - 1} + (n - 1) a_{2} x^{n - 2} + ⋯ + 2 a_{n - 1} x + a_{n}$ . 如 $f (x) = 4 x^{3} - 3 x^{2} + 5 x - 8$ ，则它的伴随多项式 $g (x) = 3 \times 4 x^{2} - 2 \times 3 x + 1 \times 5 = 12 x^{2} - 6 x + 5$ .
请根据上面的材料，完成下列问题：

(1)、已知 $f (x) = x^{5}$ ，则它的伴随多项式g(x) = .

(2)、已知 $f (x) = 5 x^{2} - 3 (9 x - 1)$ ，则它的伴随多项式g(x) = ▲ ；若g(x) = 13，求x的值.

(3)、已知二次多项式 $f (x) = (a + 3) x^{2} + 16 x + 21$ ，并且它的伴随多项式是g(x)，若关于x的方程 $g (x) = - 2 x$ 有正整数解，求a的整数值.

查看解析
7、甲、乙两支工程队修一条公路，已知甲队每天修路的长度比乙队每天修路的长度多20m，甲队修路500m与乙队修路300m用的天数相同.

(1)、求：甲、乙两支工程队每天各修路多少米？

(2)、计划修建长2400m的公路，因工程需要，甲、乙两支工程队都要参与这条路的修建.若甲队每天需要费用为1.2万元，乙队每天需要费用为0.6万元，在总费用不超过54万元的情况下，至少安排乙队施工多少天？

查看解析
8、为了了解某市某校学生对以下四个电视节目：A《中国诗词大会》、B《最强大脑》、C《朗读者》、D《出彩中国人》的喜爱情况，随机抽取了部分学生进行调查，要求每名学生选出并且只能选出一个自己最喜爱的节目，根据调查结果，绘制了如下两幅不完整的统计图.
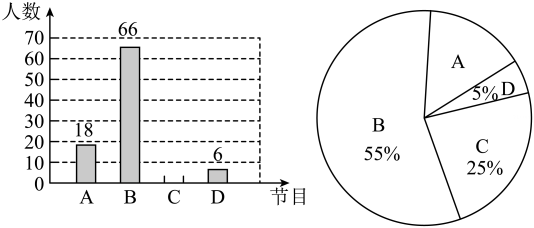
请你根据图中所提供的信息，完成下列问题：

(1)、本次调查的学生人数为；

(2)、在扇形统计图中，A部分所占圆心角的度数为；

(3)、请将条形统计图补充完整；

(4)、若该校共有2000名学生，估计该校最爱《最强大脑》的学生有多少人？

查看解析
9、如图，点E、F是平行四边形ABCD对角线AC上两点， $B E ∥ D F$ .

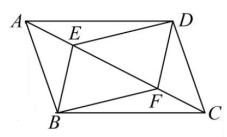(1)、求证：四边形BEDF是平行四边形；

(2)、若 $A C = 6 \sqrt{3}$ ， $B C = 8$ ， $∠ A C B = 3 0^{°}$ ，求平行四边形ABCD的面积.

查看解析
10、如图，在四边形 ABCD 中， $∠ A = ∠ C = 9 0^{°}$ .

(1)、尺规作图：作 $∠ A B C$ 的角平分线，交 AD 于点 E.（不写作法，保留作图痕迹）

(2)、画线段 $D F ∥ B E$ ，交 BC 于点 F，若 $∠ A B C = 7 0^{°}$ ，求 $∠ C D F$ .

查看解析
11、化简： $(\frac{x + 2}{x^{2} - 2 x} - \frac{x - 1}{x^{2} - 4 x + 4}) + \frac{x^{2} - 16}{x^{2} + 4 x}$ ，并从1，2，3中选择一个合适的数代入求值.

查看解析
12、解不等式组： ${\begin{array}{l} 5 x - 3 < 2 (x + 3) ① \\ \frac{x + 2}{7} \leq 0 ② \end{array}$ ，并将该不等式组的解集在数轴上表示出来.

查看解析
13、如图，线段 AB，DE 的垂直平分线交于点 C，且 $∠ A B C = ∠ E D C = 7 2^{°}$ ， $∠ A E B = 11 2^{°}$ ，则 $∠ E B D$ 的度数为.

查看解析
14、已知正整数x满足 $\frac{x - 2}{3} < 0$ ，求代数式 $(x - 2)^{115} - \frac{5}{x}$ 的值是.

查看解析
15、关于x的不等式组 ${\begin{array}{l} 6 - 2 x > 0 \\ 2 (x + a) \geq x + 3 \end{array}$ 至少有4个整数解，则a的取值范围是.

查看解析
16、若设 $4 + \sqrt{3}$ 的整数部分为a，则a的值为.

查看解析
17、如图，在四边形 ABCD 中， $A D ∥ B C$ ， $∠ A = 9 0^{°}$ ， $A D = 16$ ， $B C = 21$ ， $C D = 13$ ，动点 $P$ 从点 $B$ 出发，沿射线 BC 以每秒 $3$ 个单位的速度运动，动点 $Q$ 同时从点 $A$ 出发，在线段 AD 上以每秒 $1$ 个单位的速度向终点 $D$ 动，当动点 $Q$ 到达点 $D$ 时，动点 $P$ 也同时停止运动. 设点 $P$ 的运动时间为t（秒），以点 $P$ 、 $C$ 、 $D$ 、 $Q$ 为顶点的四边形是平行四边形时 t 值为（）秒.

A、 $2$ 或 $\frac{5}{2}$ B、 $\frac{5}{2}$ C、 $\frac{37}{4}$ 或 $\frac{5}{2}$ D、 $\frac{37}{3}$

查看解析
18、如图，等边三角形 ABC 的边长为 6cm，D、E 分别为 AC、AB边上的点， $A D = A E = 4 c m$ ，连接 DE，将 $△ A D E$ 绕点 D 逆时针旋转，得到 $△ E D P$ ，连接 CP，则 CP 的长是（）

A、 $\sqrt{3}$ cm B、 $2 \sqrt{3}$ cm C、4 cm D、 $\sqrt{2}$ cm

查看解析
19、已知点 $m_{1} (a + 1, 4)$ 和点 $m_{2} (3, b - 1)$ 关于x轴对称，则 $(a + b)^{2025}$ 的值为（）

A、0 B、-1 C、1 D、 $5^{2025}$

查看解析
20、冰柜里有四种饮料：2瓶可乐、3瓶咖啡、4瓶枯了水、6瓶汽水，其中可乐和咖啡是含有咖啡因的饮料，那么从冰柜里随机取一瓶饮料，该饮料含有咖啡因的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看解析

上一页 582 583 584 585 586 下一页跳转