版本：
全部 人教版（2024） 北师大版（2024） 浙教版（2024） 华师大版（2024） 苏科版（2024） 湘教版（2024） 青岛版（2024） 冀教版（2024） 沪科版（2024） 沪教版（五四学制）（2024） 北京课改版（2024） 人教版（五四学制） 鲁教版（五四学制）（2024）

相关试卷

  • 1、 如图，有两个完全重合的▱ABCD和▱AEFG ， 把▱AEFG绕点A按逆时针方向转动，使得点E落在▱ABCD的边CD上，连接BG，∠DAB=45° ， AB=10 ， BC=2 ， 则BG的长为（    ）

    A、102 B、10 C、5 D、25

    查看解析

  • 2、 冰裂纹是我国古典园林的传统铺装纹样之一，被广泛应用于建筑装饰和瓷器. 如图2是从图1冰裂纹铺装的路面图案中提取的多边形，则这个多边形的内角和是（    ）

    A、180° B、360° C、540° D、720°

    查看解析

  • 3、 下列等式由左边到右边的变形，属于因式分解的是（    ）
    A、m2−4=(m+2)(m−2) B、a(x+y)=ax+ay C、x2−2x+2=(x−1)2+1 D、a2−b2+1=(a+b)(a−b)+1

    查看解析

  • 4、 如图，在□ABCD中，∠A=70° ， 则∠D的度数为（    ）

    A、70° B、80° C、110° D、120°

    查看解析

  • 5、 2025年6月21日是我国二十四节气中的夏至，深圳当天最高气温是34°C ， 最低气温28°C ， 则这天气温t(°C)的变化范围是（    ）
    A、t≥28 B、t≤34 C、t=31 D、28≤t≤34

    查看解析

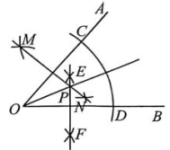
  • 6、 综合与实践
    (1)、 某数学小组用尺规作图在∠AOB内求作一点P，使得∠AOP=∠BOP.

    ①经过讨论，得到如下两种作法，补全表格中的证明过程和依据.


    方法一

    方法二

    作

    图

    步

    骤

    1. 在OA上任取一点C，作∠ACE=∠AOB.

    2. 在射线CE'上作CP=OC.

    点P即为所求.

    1.在OA和OB上分别取点C，D，使得OC=OD.

    2. 作OD的垂直平分线EF.

    3. 作 OC 的垂直平分线 MN，与直线 EF 交于点 P.

    点 P 即为所求.

    图

    示

    理

    由

    证明：∵∠ACE=∠AOB ， （已作）

    ∴CP∥OB ， （▲）

    ∴∠CPO=▲.

    ∵CP=OC ， （已作）

    ∴∠CPO=▲ ，

    ∴∠AOP=∠BOP.

    证明：连接PC，PD.

    ∵EF垂直平分OD，（已作）

    ∴OP=▲ ，

    同理可得OP=PC，

    ∴PC=PD.

    又∵OC=OD（已作），PO=PO，

    ∴△OPC≅△OPD ， （▲）

    ∴∠AOP=∠BOP.

    ②请你用不同于上面的尺规作图方法在图1中求作点P（保留作图痕迹，不写作法），并说明作法的正确性.

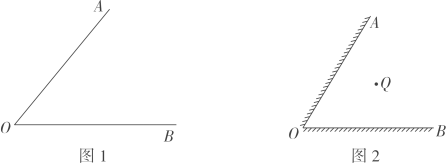    (2)、 在制作万花筒时，可以先将两面镜子的背面用胶带粘贴形成一个可以自由开合的“镜子门”.如图2，设两面镜子的夹角∠AOB=60° ， 物体Q在∠AOB的角平分线上，则在镜子中一共形成个物体Q的像.

    查看解析

  • 7、【定义】
    一个正整数除以它的各位数字之和，所得的商叫做这个数的平均商.

    例如：5的平均商=55=1 ， 24的平均商=242+4=4 ， 312的平均商=3123+1+2=52.

    (1)、【理解】
    8的平均商为 ， 55的平均商为；
    (2)、【探究】
    数学兴趣小组开展研究，首先计算部分两位数的平均商（保留两位小数），结果如下表：

     

    9

    8

    7

    ⋯

    1

    0

    9

    5.5

    5.76

    6.06

    ⋯

    9.1

    10

    8

    5.24

    5.5

    5.8

    ⋯

    9

    10

    7

    4.94

    5.2

    5.5

    ⋯

    8.88

    10

    老师：“请同学们观察表格，谈谈你的发现.”

    小明：“我发现，个位数字与十位数字相同的两位数的平均商相同.”

    小莉：“我发现，当个位数字相同时，十位数字越小，平均商越小.”

    ①请你再写出一条新的发现.

    ②假设一个两位数的个位数字与十位数字都为a，请结合计算，说明小明的说法是否合理.

    (3)、【拓展】
    利用上述研究思路，可以得出平均商最小的三位数是.

    查看解析

  • 8、如图，点B，E，C，F在同一条直线上，AC，DE相交于点G，AB=DE ， AB∥DE ， BE=CF.

    (1)、 求证：AC∥DF；
    (2)、 若∠B=45° ， ∠F=60° ， 求∠EGC的度数.

    查看解析

  • 9、打羽毛球时，羽毛球的运动轨迹主要受击球力度、角度和空气阻力影响.小明发了个高远球，羽毛球到达最高点后开始下落.羽毛球高度与下落时间的关系如下表所示：

    下落时

    间t(s)

    0

    0.2

    0.4

    0.6

    0.8

    1

    1.2

    1.4

    1.6

    1.8

    2

    羽毛球高

    度h(m)

    5.25

    5.17

    4.96

    4.63

    4.19

    3.66

    3.05

    2.37

    1.63

    0.74

    0

    根据表格所提供的信息，回答下列问题：

    (1)、 在这个变化过程中，自变量是 ， 因变量是；
    (2)、 当下落时间为 s时，羽毛球高度为3.66m；
    (3)、 当下落时间为1.2s时，羽毛球下降的距离为 m；
    (4)、 假设搭档小华的接球合适高度在2m左右，从羽毛球下落那一刻算起，小华最好在 s内完成回击.

    查看解析

  • 10、如图，小深每天乘坐公交车上学需经过由南往北的路口，该路口信号灯的配时周期为113s，其中包含：红灯80s，绿灯30s，黄灯3s.
    (1)、小深乘坐公交车到达该路口时，遇到红灯的概率为；遇到绿灯的概率为；
    (2)、为提高通行效率，交管部门计划将配时周期（113秒）缩短.根据交通管理规范，该路口配时周期宜设置在80秒到100秒之间.请你设计一个符合规范的红绿灯配时方案，使得行人遇到红灯的概率是遇到绿灯的概率的3倍，并说明理由.（配时周期内黄灯时长不变，红绿灯时长为整数）

    查看解析

  • 11、先化简，再求值：[(a+2b)2+(a+2b)(a−2b)]÷2a ， 其中a=2 ， b=−1.

    查看解析

  • 12、计算：
    (1)、a⋅a5+(a3)2−a8÷a2；
    (2)、(a+2b)(3a+b).

    查看解析

  • 13、 如图，在△ABC中，∠ACB=90° ， AC=BC ， D为平面上一点，AD⊥DC ， 若CD=6 ， 则△BCD的面积为.

    查看解析

  • 14、 若 a3−a2+a−1=0 ， 则 a4 的值为.

    查看解析

  • 15、 运动生理学实验发现，跳绳所消耗的卡路里(Cal)=0.0024×体重（kg）×跳绳次数.一名体重50kg的学生跳绳x次，他所消耗的卡路里y（单位：Cal）与x（单位：次）之间的关系式为：.

    查看解析

  • 16、如图，两条直线a，b被第三条直线c所截，请添加一个条件：使得a∥b.

    查看解析

  • 17、 抛一个瓶盖，落地后会出现“盖口向上”和“盖口向下”两种情况.小明通过信息技术模拟实验得到了如下的折线统计图.根据统计结果估计事件“盖口向上”发生的概率为.

    查看解析

  • 18、 如图，△ABC的各边中点分别为D，E，F，AD与EF相交于点O，将三角形分为四个部分，面积分别为S1 ， S2 ， S3 ， S4 ， 则S1+S3>S2+S4的大小关系为（    ）

    A、S1+S3>S2+S4 B、S1+S3=S2+S4 C、S1+S3<S2+S4 D、无法确定

    查看解析

  • 19、如图，AB=AD ， AC=AE ， ∠BAE=∠DAC ， 下列结论不一定成立的是（    ）

    A、AF=EF B、∠C=∠E C、BC=DE D、∠B=∠D

    查看解析

  • 20、 如图，直线l的同侧有P，Q两点，在直线l上确定一个点，使得这个点到P，Q两点距离之和最短，这个点是（    ）

    A、点A B、点B C、点C D、点D

    查看解析

上一页 505 506 507 508 509 下一页 跳转