相关试卷

1、如图，在平面直角坐标系 $x O y$ 中，直线 $l : y = k x + 2$ 与 $x, y$ 轴分别相交于点A，B，与反比例函数 $y = \frac{m}{x} (x ＞ 0)$ 的图象相交于点C，已知 $O A = 1$ ，点C的横坐标为2．

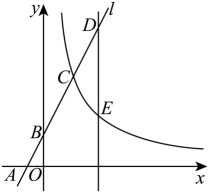(1)、求 $k, m$ 的值；

(2)、平行于 $y$ 轴的动直线与 $l$ 和反比例函数的图象分别交于点D，E，若以B，D，E，O为顶点的四边形为平行四边形，求点D的坐标．

查看解析
2、如图，矩形 $A O B C$ 的边 $O A = 3$ ， $O B = 4$ ，动点F在边BC上（不与B、C重合），过点F的反比例函数 $y = \frac{k}{x}$ 的图象与边 $A C$ 交于点E，直线EF分别与y轴和x轴相交于点D和G．给出下列命题：①若 $k = 6$ ，则 $△ O E F$ 的面积为 $\frac{9}{2}$ ；②若 $k = \frac{21}{8}$ ，则点C关于直线EF的对称点在x轴上；③满足题设的k的取值范围是 $0 ＜ k \leq 12$ ；④若 $D E \cdot E G = \frac{25}{6}$ ，则 $k = 2$ ；其中正确的命题个数是（）

A、1个 B、2个 C、3个 D、4个

查看解析
3、如图，点 $A 、 C$ 为反比例函数 $y_{1} = - \frac{6}{x}$ 上的动点，点B、D为反比例函数 $y_{2} = \frac{2}{x}$ 上的动点，若四边形 $A B C D$ 为菱形，则该菱形边长的最小值为．

查看解析
4、如图，正方形四个顶点分别位于两个反比例函数 $y = \frac{3}{x}$ 和 $y = \frac{n}{x}$ 的图象的四个分支上，则实数 $n$ 的值为（）

A、-3 B、 $- \frac{1}{3}$ C、 $\frac{1}{3}$ D、3

查看解析
5、如图，在平面直角坐标系 $x O y$ 中，直线 $y = - x + 5$ 与y轴交于点A，与反比例函数 $y = \frac{k}{x}$ 的图象的一个交点为 $B (a, 4)$ ，过点B作AB的垂线l．

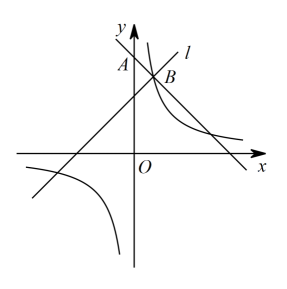(1)、求点A的坐标及反比例函数的表达式；

(2)、若点C在直线l上，且 $△ A B C$ 的面积为5，求点C的坐标；

(3)、P是直线l上一点，连接PA，以P为位似中心画 $△ P D E$ ，使它与 $△ P A B$ 位似，相似比为m．若点D，E恰好都落在反比例函数图象上，求点P的坐标及m的值．

查看解析
6、如图，在平面直角坐标系 $x O y$ 中，直线 $y = k x + b$ 与x轴交于点 $A (4, 0)$ ，与y轴交于点 $B (0, 2)$ ，与反比例函数 $y = \frac{m}{x}$ 在第四象限内的图象交于点 $C (6, a)$ ．

(1)、求反比例函数的表达式：

(2)、当 $k x + b ＞ \frac{m}{x}$ 时，直接写出x的取值范围；

(3)、在双曲线 $y = \frac{m}{x}$ 上是否存在点P，使 $△ A B P$ 是以点A为直角顶点的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

查看解析
7、如图，正比例函数y=-3x与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于A， $B (1, m)$ 两点，点C在x轴负半轴上， $∠ A C O = 45 °$ ．

(1)、 $m =$ ， $k =$ ，点C的坐标为．

(2)、点P在x轴上，若以B，O，P为顶点的三角形与 $△ A O C$ 相似，求点P的坐标．

查看解析
8、如图，一次函数 $y = 2 x$ 与反比例函数 $y = \frac{2}{x}$ 的图象相交于 $A 、 B$ 两点，以 $A B$ 为边作等边三角形 $A B C$ ，若反比例函数 $y = \frac{k}{x}$ 的图象过点 $C$ ，则 $k$ 的值为．

查看解析
9、如图， $△ A B C$ 是等腰三角形， $A B$ 过原点 $O$ ，底边 $B C ∥ x$ 轴，双曲线 $y = \frac{k}{x}$ 过 $A ， B$ 两点，过点 $C$ 作 $C D ∥ y$ 轴交双曲线于点 $D$ ，若 $S_{△ B C D} = 12$ ，则 $k$ 的值是（）

A、-6 B、-12 C、 $- \frac{9}{2}$ D、 $- 9$

查看解析
10、【综合探究】探究小组用两个完全相同的等腰直角三角形纸片通过平移做实验.

(1)、【操作探究】如图1，把重合中的 $△ A B C$ 向左平移成 $△ D E F$ ，顶点E恰好是BC边的中点，连接AF， $A B = 2 \sqrt{5}$ ，求三角形ACF的面积；

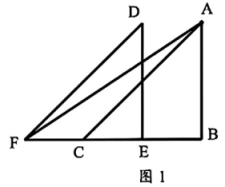(2)、【深入探究】如图2，把 $△ D E F$ 继续向左平移，当点E与点C重合时，连接AF交DC于点G，求证：DG=CG；

(3)、【拓展提升】如图3，在(2)的条件下，过点D作 $D Q ⊥ A F$ 于点Q，连CQ，DQ=2，直接写出CQ的长度.

查看解析
11、【综合与实践】
深圳某条东西方向的道路共有五车道，早晚高峰期间经常拥堵，数学兴趣小组的同学就此问题开展研究性学习活动.
【信息一】通过实地考察，兴趣小组的同学对该路段的交通量（辆/分钟）和时间进行数据的收集统计和分析，整理得到下列表格，发现时间和交通量的变化规律符合一次函数特征，并由此得到 $y_{1}$ 与x的函数关系式及 $y_{2}$ 与x的函数关系式
时间x
7时
10时
14时
17时
20时
自西向东交通量 $y_{1}$ （辆/分钟）
93
78
a
43
28
自东向西交通量 $y_{2}$ （辆/分钟）
42
48
56
62
68
【信息二】兴趣小组的同学希望根据两个不同方向的拥堵情况来合理设置中间“可变车道”的方向. 通过查阅资料发现：若单位时间内双向交通总量设为 $v_{总} = y_{1} + y_{2}$ ，当车流量较大的方向的交通量 $y \geq \frac{2}{3} v_{总}$ 时，道路非常拥堵，需要通过把“可变车道”的行车方向与交通量较大的方向变为相同，去改善交通状况.
【解决问题】

(1)、已知 $y_{1}$ 与x之间的函数关系式为 $y_{1} = - 5 x + 128$ ，表格中 $a$ =；

(2)、求 $y_{2}$ 与x之间的函数系式（不写自变量的取值范围）；

(3)、请你通过计算判断该路段从7时至20时在比较拥堵时如何设置“可变车道”的方向以缓解交通拥堵？（即在什么时间段把“可变车道”设为哪个方向的车道）

查看解析
12、 2025 全球人工智能终端展暨第六届深圳国际人工智能展览会 5 月在深圳会展中心启幕，人工智能的迅速发展为物流运输和配送带来了巨大便利. 某快递公司的仓库主要使用 A， B 两种不同型号的分拣机器人，已知 A 型机器人比 B 型机器人每小时多分拣快递 200 件，且 A 型机器人分拣 10000 件快递所用时间与 B 型机器人分拣 9000 件所用时间相等.

(1)、 A， B 型机器人每小时各分拣快递多少件?

(2)、 “618”期间，快递公司的业务量猛增，每天有 25000 件快递要分拣， A， B 型机器人一起工作 5 小时后， B 型机器人有其他业务要处理，剩下的快递由 A 机器人分拣，请问 A 型机器人还要工作多少个小时才能完成任务?

查看解析
13、如图， $▱ A B C D$ 的对角线AC与BD交于点 $O$ ，点 $E$ 、 $F$ 分别在OB、OD上.

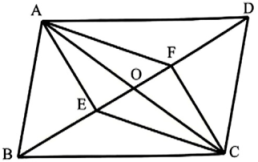(1)、下列条件：① $B E = D F$ ；② $A F ∥ C E$ ；③ $∠ A E B = ∠ C F D$ ，请你从中选择一个能证明四边形AECF是平行四边形的条件，并写出证明过程；

(2)、若四边形AECF是平行四边形， $∠ A D B = 3 0^{°}$ ， $A E ⊥ B D$ ，垂足为点 $E$ ， $A D = 4$ ， $D F = \sqrt{3}$ ，求 $▱ A E C F$ 的面积.

查看解析
14、如图， $△ A B C$ 三个顶点的坐标分别为A(1，1)，B(4，2)，C(3，4).
⑴请画出 $△ A B C$ 向下平移5个单位长度后得到的 $△ A_{1} B_{1} C_{1}$ ；
⑵请画出 $△ A B C$ 关于原点成中心对称的 $△ A_{2} B_{2} C_{2}$ ；
⑶在y轴上求作一点P，使 $△ P A B$ 的周长最小.

查看解析
15、小颖和小红在化简 $(\frac{1}{x + 2} + \frac{1}{x - 2}) \cdot \frac{x^{2} - 4}{x^{2}}$ 的过程中，分别给出如下的部分运算过程.
小颖：原式= $[\frac{x - 2}{(x + 2) (x - 2)} + \frac{x + 2}{(x + 2) (x - 2)}] \cdot \frac{x^{2} - 4}{x^{2}}$
··· $⋯ ⋯$
小红：原式= $\frac{1}{x + 2} \cdot \frac{x^{2} - 4}{x^{2}} + \frac{1}{x - 2} \cdot \frac{x^{2} - 4}{x^{2}}$

(1)、小颖解法的依据是（），小红解法的依据是（）
A. 分式的基本性质
B. 等式的基本性质
C. 乘法结合律
D. 乘法分配律

(2)、请你选择一种解法，写出完整的解答过程，并从“-2，1，2”中选一个合适的数作为x的值，代入求该分式的值.

查看解析
16、

(1)、解不等式组： ${\begin{array}{l} 3 x - 1 \leq 5 ① \\ \frac{x}{2} > - 1 ② \end{array}$ ，并把不等式组的解集在数轴上表示出来.

(2)、解分式方程： $\frac{1 - x}{x - 2} = \frac{1}{2 - x} - 2$

查看解析
17、如图1，在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ 于点D，点P从点B出发，沿 $B \to A \to D \to C$ 的方向匀速运动到点C，速度为1cm/s，图2是点P运动时， $△ A P C$ 的面积y（ $c m^{2}$ ）随时间x(s)变化的图象，则a的值为.

查看解析
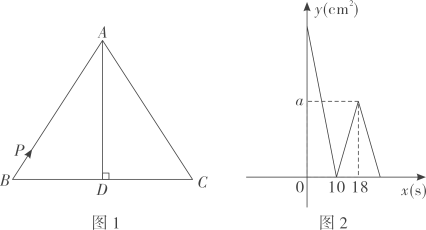
18、如果某商品降价 $x %$ 后的售价为a元，那么该商品的原价为元.

查看解析
19、人字梯及其侧面如图所示，AB，AC为支撑架，DE为拉杆，D，E分别是AB，AC的中点，若 $D E = 50 c m$ ，则B，C两点的距离为cm.

查看解析
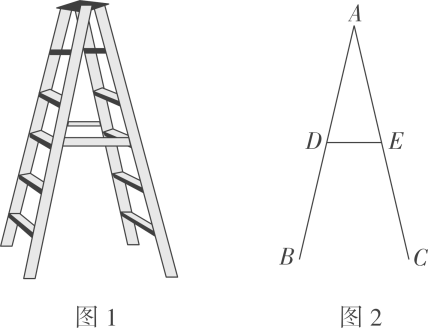
20、苯（分子式为 $C_{6} H_{6}$ ）的环状结构是由德国化学家凯库勒提出的. 随着研究的不断深入，发现如图1的一个苯分子中的6个碳原子形成了正六边形的结构，其示意图如图2，点O为正六边形ABCDEF对角线AD的中点，连接OC. 若 $O C = 1$ ，则CD的长是.

查看解析

上一页 504 505 506 507 508 下一页跳转

时间x	7时	10时	14时	17时	20时
自西向东交通量 $y_{1}$ （辆/分钟）	93	78	a	43	28
自东向西交通量 $y_{2}$ （辆/分钟）	42	48	56	62	68