相关试卷

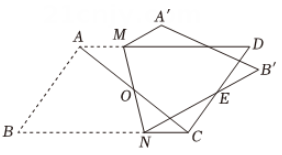
1、如图，点O是□ABCD对角线AC的中点，沿过点O的直线MN将口ABCD折叠，使点A，B分别落在A'、B'处，NB'交CD与点E，若点E是CD的中点，NC=3，NB =7，则EB'=.

查看解析
2、如图，在平面直角坐标系中，正方形ABCD的点A在x轴上，点B在y轴上，点D的坐标为（3，2）. 若反比例函数y= $\frac{k}{x}$ （k>0）在第一象限的图象经过正方形的顶点C.则k的值为.

查看解析
3、如图，在△ABC中，FG//DE// BC，AF =FD =DB，若FG=2，则BC=.

查看解析
4、已知二次函数图象与x轴的一个交点坐标为（4，0），顶点坐标为（1，1），则该二次函数的解析式为.

查看解析
5、样本数据5，6，7，8，9的方差S²=.

查看解析
6、如图，在 Rt△ABC中，∠ACB=90°，分别以边AC、BC向外作正方形ACDE和正方形BFGC，连接EF、AF.若已知AB²-AC²的值，则能求出的三角形面积是（）.

A、三角形ABF B、三角形 ACF C、三角形 AEF D、三角形 ABC

查看解析
7、为更好地开展劳动教育，学校决定在操场划出一块面积为480m²的长方形场地作为劳动基地若长方形场地的一边靠墙（墙足够长），另外三边由总长为70m的第笆围成，并且在平行于墙的边上设置两个开口宽为1m的进出门（如图），设靠墙的长方形边长为x（m），则下列方程正确的是（），

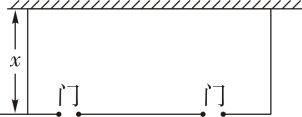A、x（72-2x）=480 B、x（68-2x）=480 C、x（72-x）=480 D、x（68-x）=480

查看解析
8、如图，O是□ABCD对角线的交点.已知∠OAD的周长为50，BD=32，AC=24，则BC的长为（）.

A、18 B、20 C、22 D、26

查看解析
9、如图，已知A是反比例函数 $y = \frac{k}{x}$ 上一点，AB⊥y轴与点B，点C在x轴上，且∠ABC的面积为1，则k的值为（）.

A、 $\frac{1}{2}$ B、1 C、4 D、-2

查看解析
10、车间有15名工人，某一天他们生产的机器零件个数统计如下：
生产零件个数（个）
6
7
8
9
10
11
13
15
16
工人人数（人）
1
2
4
1
2
1
1
2
1
则工人生产的机器零件的中位数和众数分别是（）.

A、7，10 B、8，10 C、8，9 D、9，8

查看解析
11、抛物线y=-x²-4x+m的对称轴为（）.

A、直线x=-2 B、直线x=2 C、直线x=4 D、直线x=-4

查看解析
12、如图，在四边形ABCD中，AB⊥BC，∠A=∠C=100°，则∠D的度数是（）.

A、60° B、70° C、80° D、90°

查看解析
13、一元二次方程9x²＝5-4x化为一般形式后，二次项系数、一次项系数、常数项分别是（）

A、9，5，-4 B、9，4，-5 C、9，-5，4 D、9，-4， 5

查看解析
14、化简： $\sqrt{（ - 2)^{2}}$ 的结果是（）.

A、-4 B、-2 C、2 D、4

查看解析
15、点A，B为坐标轴上两点，点C为坐标平面内一点，OA=OB，连接AB，OC，AC，BC.

(1)、如图1，点C在△OAB内，满足∠OCA= 90°.
①若∠OAC =35°，求∠BOC的度数；
②若S_△_OBC =18，求OC 的长；

(2)、如图2，点C在y轴的正半轴上，满足OC= $\frac{1}{4}$ OB，点P在线段OA上，连接 BP并延长至点D，使得DP=BP，连接AD，若AD⊥AC，点A的坐标为（t，0），求点P的坐标（用含t的式子表示）.

查看解析
16、对于不等式组，根据它的解集是否能取到最大数与最小数，可分为四种类型，我们不妨约定：
既能取到最大数，也能取到最小数的不等式组称为“峰谷”不等式组，其中最大数称为峰值，最小数称为谷值；
只能取到最大数，不能取到最小数的不等式组称为“峰”不等式组，其中最大数称为峰值；
只能取到最小数，不能取到最大数的不等式组称为“谷”不等式组，其中最小数称为谷值；
既不能取到最大数，又不能取到最小数的不等式组称为“非峰非谷”不等式组。

(1)、判断下列不等式组的类型，将字母（A“峰谷”不等式组；B“峰”不等式组；C“谷”不等式组；D“非峰非谷”不等式组）写在括号内：
①不等式组 ${\begin{array}{l} x - 1 > 0 \\ 2 x \leq 4 \end{array}$ （    ）
②不等式组 ${\begin{array}{l} x - 2 \leq 2 x \\ x - 1 \leq - x \end{array}$ （    ）
③不等式组 ${\begin{array}{l} x - 1 > - 1 \\ x + 1 < 2 \end{array}$ （    ）

(2)、若关于x的不等式组 ${\begin{array}{l} x + 1 > 2 a \\ x + a \geq 2 \end{array}$ 是“谷”不等式，求关于x的不等式 $a x + 1 > x + a$ 的解集；

(3)、若关于x的不等式组 ${\begin{array}{l} m x \geq 2 \\ 2 x \leq m + 5 \end{array}$ 是“峰谷”不等式组，且该不等式组的峰值、谷值均为整数，此时关于y的不等式组 ${\begin{array}{l} \frac{1 - y}{2} \leq \frac{1 + y}{3} + m \\ 2 (y + n) > 1 + 3 y \end{array}$ 有4个整数解，求n的取值范围.

查看解析
17、在经济新风向吹拂下，“地摊经济”正散发着无限可能，小明准备去批发市场购进一批花盆和种子、已知购买1个花盆、2包种子共需6元，购买2个花盆、3包种子共花费11元。

(1)、求花盆和种子的单价；

(2)、小明准备购进x个花盆（0<x<90），90包种子，批发店给出以下优惠方案：
方案一：花盆和种子都按9折优惠：
方案二：买一个花盆送一包种子，剩余的种子按原价购买。
①求两种方案所需的费用（用含x的式子表示）：
②请你帮小明选择哪种方案更省钱？

查看解析
18、如图， CA=CD，∠1= ∠2，BC=EC、

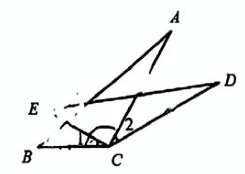(1)、求证： AB= DE

(2)、若AB与 DE 的交点为M，∠1=30°，求∠EMB的度数.

查看解析
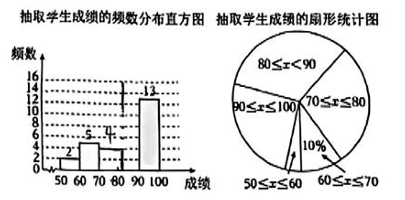
19、雨花区某小区为了解居民对“垃圾分类知识”的掌握情况，从小区班机抽取部分居民进行测试，并对成绩（百分制）进行整理、描述和分析，下面给出部分信息：
①学生成绩的统计图如图（数据分为五组：50≤x<60，60≤x<70，70≤x<80，80≤x<90，90≤x≤100）·
②80≤x<90这一组成绩是 80、80、80、81、81、82、83、84、84、85、85、87、88、89、89、89.
③成绩不低于90分为优秀.
根据以上信息，回答下列问题：

(1)、本次调查采用的方式是（选填“全面调查”或“抽样调查”）；

(2)、补全频数分布直方图；

(3)、求出成绩在60≤x<70这一组所在扇形的圆心角度数：

(4)、若该小区共有400名居民，请估计达到优秀的人数.

查看解析
20、如图，在平面直角坐标系xOy中，△ABC三个顶点的坐标分别是A（-2，3），B（-4，-1），C（-1，1），将△ABC平移，使点B与点O重合，得到△A'OC'，其中点A，C的对应点分别为A'，C'.

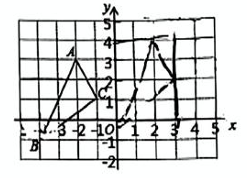(1)、画出△A'OC'：

(2)、写出点A'，C'的坐标；

(3)、求△A'OC' 的面积.

查看解析

上一页 489 490 491 492 493 下一页跳转

生产零件个数（个）	6	7	8	9	10	11	13	15	16
工人人数（人）	1	2	4	1	2	1	1	2	1