-
1、 下列等式中,从左到右的变形属于因式分解的是( )A、 B、 C、 D、
-
2、 下列分式是最简分式的是( )A、 B、 C、 D、
-
3、 已知 , 则下列不等式一定成立的是( )A、 B、 C、 D、
-
4、 下列由 AI 设计的四组图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
5、阅读理解:
定义:若分式和分式满足(为正整数),则称是的“差分式”.
例如:我们称是的“差分式”,
解答下列问题:
(1)、分式是分式的“ 差分式”.(2)、分式 是分式的“差分式”.① (含的代数式表示);
②若 的值为正整数,为正整数,求的值.
(3)、已知 , 分式是的“差分式”(其中为正数),求的值. -
6、如图1所示是一种简易手机支架,由底座、支撑板和托架组成,将手机放置在托架上,图2是其简易结构图.现测量托架长长 , 支撑板长 , 可绕点转动,可绕点转动.
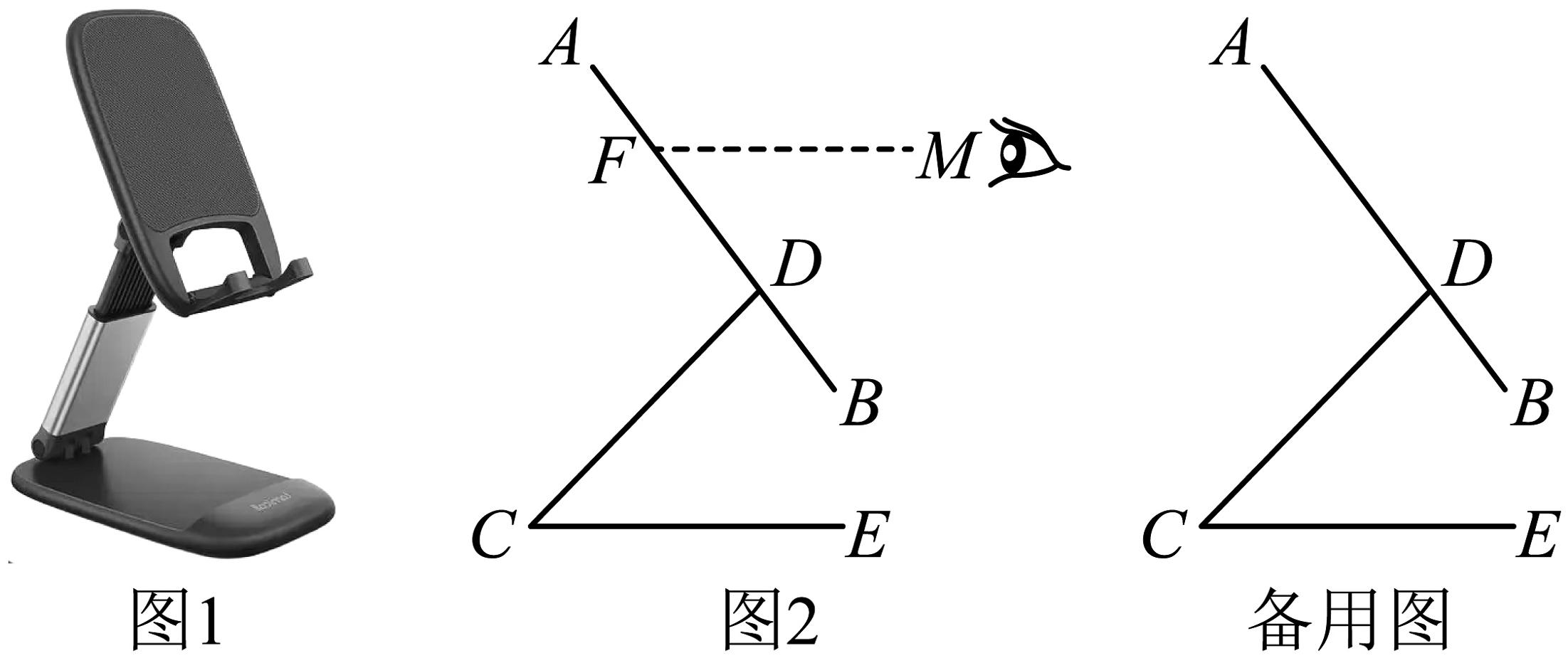 (1)、若水平视线与的夹角 , , 求的度数;(2)、当 , 时,求点到底座的距离.(结果精确到0.1,参考:)
(1)、若水平视线与的夹角 , , 求的度数;(2)、当 , 时,求点到底座的距离.(结果精确到0.1,参考:) -
7、某校举办了数学知识竞赛,从七、八年级各随机抽取了10名学生的竞赛成绩(百分制),进行整理,描述和分析如下:成绩得分用表示(为整数)共分成四组: . ; . ; . ; . .
七年级10名学生的成绩是:82,86,86,88,90,96,96,96,100,100.
八年级10名学生的成绩在组中的数据是:90,94,94.
抽取的七、八年级学生成绩统计表:
年级
平均数
中位数
众数
七年级
八年级
92
94
100
根据以上信息,解答下列问题:
(1)、直接写出图表中 , 的值:______,______,______.(2)、由表格中数据可推出,八年级这10名同学中,成绩在组()的人数有______人.(3)、若八年级参加竞赛的学生共100人,估计八年级参加竞赛成绩在组()的学生人数. -
8、计算: .
-
9、已知 , 满足 , 则的值为 .
-
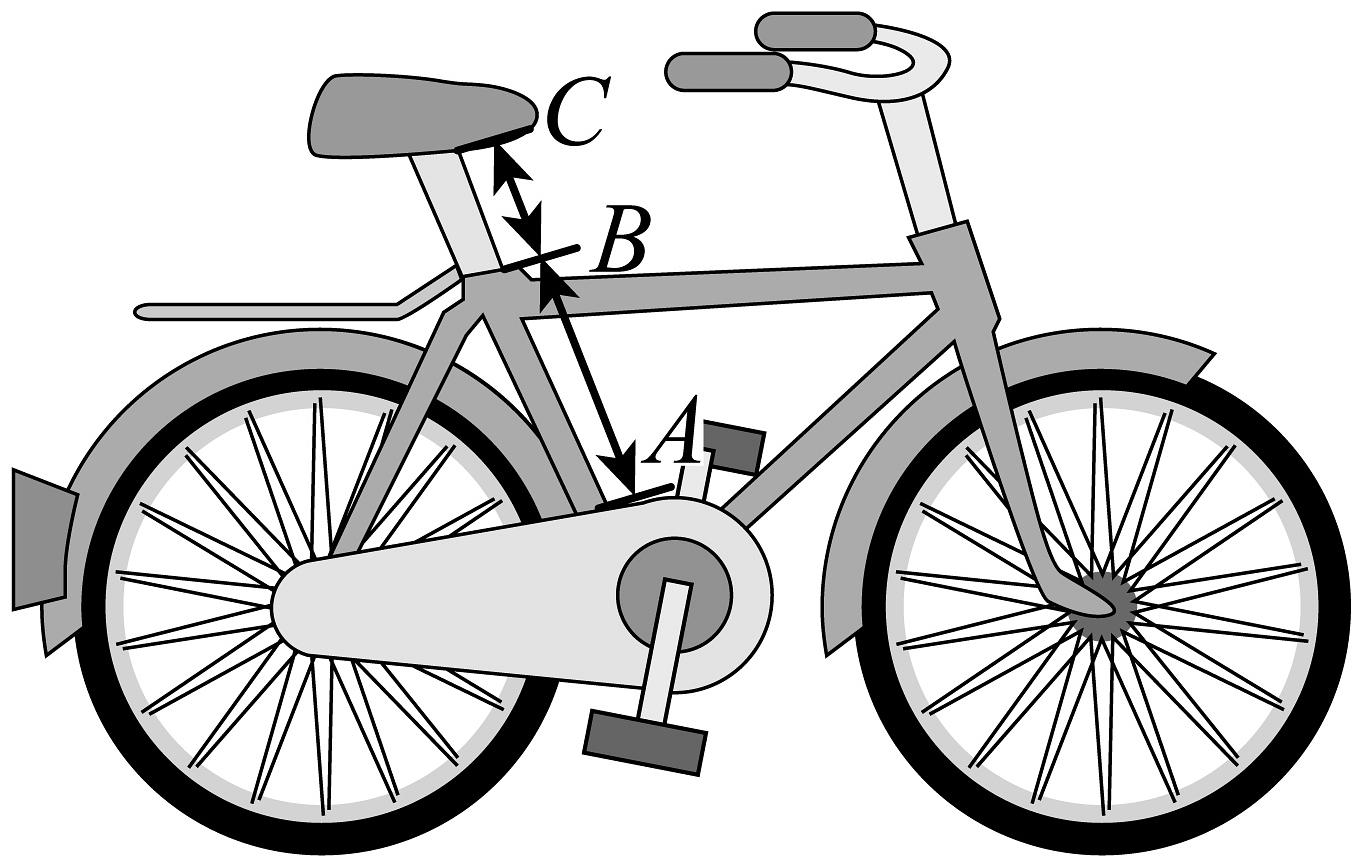
10、骑自行车可以放松心情,是一种非常好的“黄金有氧运动”.骑行过程中,如果车座高度不合适,会使骑行者踩踏费力,甚至造成膝盖磨损.有一种测量方法:双腿(不穿鞋)站立,测量档部离地面的距离(单位:),得出的数据乘0.883就是相应的骑行时最合适的长度(由长度为的立管和可调节的坐杆组成,如图所示).若设长度最合适时坐杆的长度为 , 则与之间的关系式为 .
-
11、如图,正方形的对角线、相交于点 , 且 , 正方形的顶点与点重合,边与重合,将正方形绕点顺时针旋转 , 与边交于点 , 与边交于点 , 连接交于点 , 在整个运动过程中,则点经过的路径长是( )
 A、1 B、 C、 D、
A、1 B、 C、 D、 -
12、如图,已知 , 分别是反比例函数与 , 且轴,点的坐标为 , 分别过点 , 作轴于点 , 轴于点 . 若四边形的面积为 , 则的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、月球车工作时所需的电能都是由太阳能电池板提供的.当太阳光线垂直照射在太阳光板上时,接收的太阳光能最多,某一时刻太阳光的照射角度如图所示,如果要使此时接收的太阳光能最多,那么应将太阳光板绕支点顺时针旋转的最小角度为( )
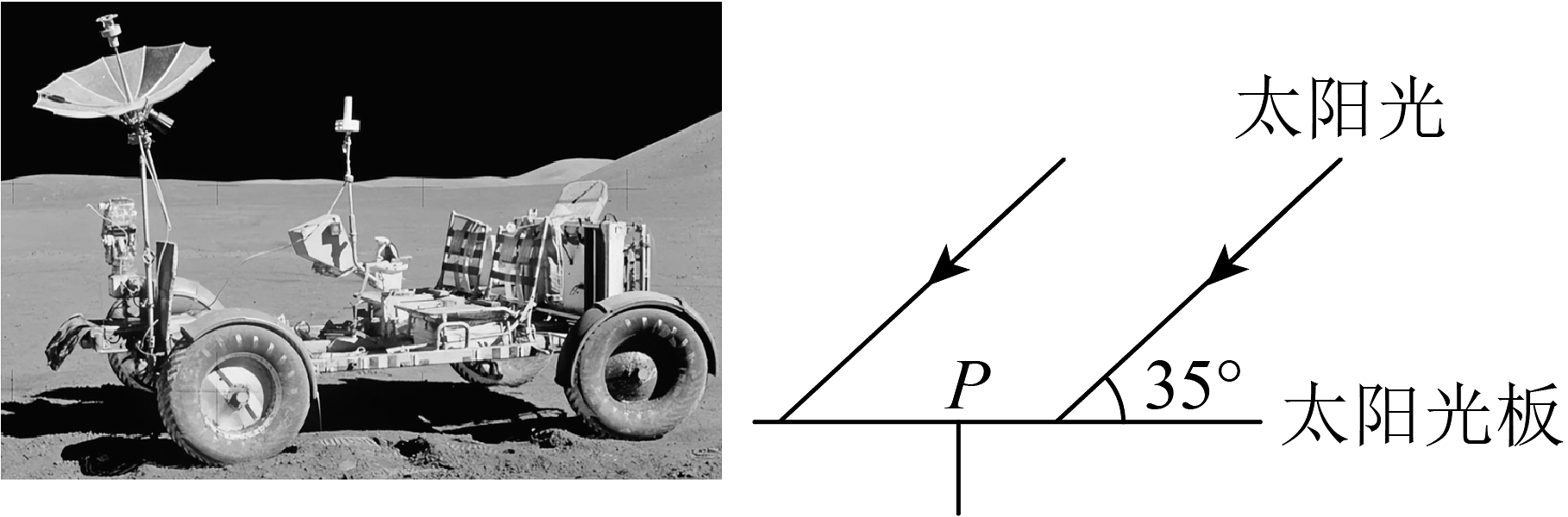 A、 B、 C、 D、
A、 B、 C、 D、 -
14、如图,在平面直角坐标系中,如果点的位置用表示,点的位置用表示,那么表示的位置是( )
 A、点 B、点 C、点 D、点
A、点 B、点 C、点 D、点 -
15、已知不等式组有解,则a的取值范围为( )A、 B、 C、 D、
-
16、下列运算正确的是( )A、 B、 C、 D、
-
17、如图是由两个圆柱组成的几何体,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
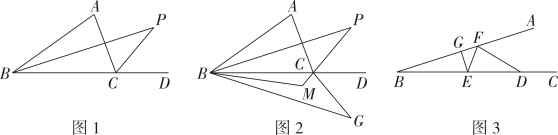
18、将一副三角板中的两块直角三角板如图1放置,PQ//MN,∠ACB=∠EDF=90°,∠ABC=∠BAC=45°,∠DFE=30°,∠DEF=60°
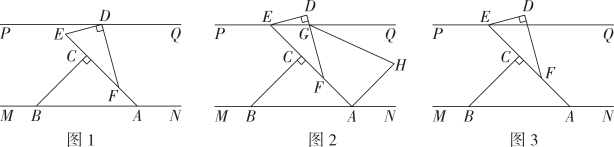 (1)、若三角板如图1摆放时,则∠PDE=.(2)、如图2,固定三角形ABC的位置不变,将三角形DEF沿AC方向平移,使得E点恰好落在PQ上, DF与直线 PQ交于点G.点H在∠AFG内部且在直线PO、MN之间; ∠FGH=2∠HGQ,∠FAH=2∠HAN,求∠H的值:(3)、如图3,两个三角板如题(2)中的位置摆放,将△DEF绕点E以每秒3°的速度逆时针旋转,同时△ABC绕点A以每秒2°的速度顺时针旋转,边ED与射线BP重合时两个三角形停止转动,当DF与△ABC的一条边平行时,直接写出符合条件的t的值..
(1)、若三角板如图1摆放时,则∠PDE=.(2)、如图2,固定三角形ABC的位置不变,将三角形DEF沿AC方向平移,使得E点恰好落在PQ上, DF与直线 PQ交于点G.点H在∠AFG内部且在直线PO、MN之间; ∠FGH=2∠HGQ,∠FAH=2∠HAN,求∠H的值:(3)、如图3,两个三角板如题(2)中的位置摆放,将△DEF绕点E以每秒3°的速度逆时针旋转,同时△ABC绕点A以每秒2°的速度顺时针旋转,边ED与射线BP重合时两个三角形停止转动,当DF与△ABC的一条边平行时,直接写出符合条件的t的值.. -
19、翻折是一种常见的图形变换,请利用对称和角平分线的知识解将下列问题:
 (1)、如图1. 在△ABC中,点D在BC的延长线上:∠ABC的角平分线与∠ACD的角平分线相交于点P.
(1)、如图1. 在△ABC中,点D在BC的延长线上:∠ABC的角平分线与∠ACD的角平分线相交于点P.①若∠ACP=55°∠ABP=20°求∠A的度数
②如图2,将△PBC以直线BC为对称轴翻折得到△GBC,∠GBC的角平分线与∠GCB的角平分线交于点M请写出∠M与∠A的数量关系,并说明理由;
(2)、 如图, ∠ABC=γ(γ<30° ), 点D为BC上一定点, 点E为BC上一动点, F、G为BA 上两动点,当GE+EF+FD最小时,直接写出∠EFD+∠GEF的值(用含有γ的代数式表示), -
20、已知方程组的解x为非正数,y为负数.(1)、求a的取值范围;(2)、在a的取值范围中,求当a为何整数时,不等式的解为?