-
1、 一次知识竞赛共有20道选择题，答对一题得5分；答错或不答，每题扣1分．要使总得分不少于88分，则至少要答对几道题？若设答对x道题，可列出的不等式为 ．
-
2、（m-3）x+2y|m-2|+6=0是关于x，y的二元一次方程，则m= ．
-
3、 已知点（a-1，2b-4）在y轴上，点B（3a-6，b+4）在x轴上，则点C（a，b）的坐标为 ．
-
4、如图，∠C+∠D=180°，∠A-∠B=90°，则∠B= ．
-
5、 （-0.6）2的平方根是 ．
-
6、已知 ， =11.108，则=（ ）A、35.12 B、351.2 C、111.08 D、1110.8
-
7、如图，添加下列一个条件后，不能判定BC∥AD的是（ ）
A、∠1=∠2+∠3 B、∠2=∠4 C、∠3=∠5 D、∠D+∠4+∠5=180° -
8、 2024年我市约有6.6万名学生参加中考，为了了解这些考生的数学成绩，从中抽取2000名考生的数学成绩进行统计分析．在这个问题中，下列说法正确的是（ ）A、我市6.6万名考生的全体是总体 B、每个考生是个体 C、2000名考生是总体的一个样本 D、样本容量是2000
-
9、已知a＜b，b＜c，那么下列式子中不一定成立的是（ ）A、a＜c B、a+c＜b+c C、a-c＜b-c D、ac＜bc
-
10、甲、乙、丙三种商品，若购买甲3件、乙2件、丙1件，共需270元；购买甲1件、乙2件、丙3件，共需242元，那么购买甲、乙、丙三种商品各一件共需（ ）A、128元 B、130元 C、150元 D、160元
-
11、如图，AB⊥BC，DB⊥AC，下列线段的长能表示点B到AC的距离的是（ ）
A、AB B、BD C、BC D、AD -
12、已知直线AB和CD相交于点O，∠COE=90°，OF平分∠AOE，∠COF=34°，则下列结论中：①∠EOF=56°；②∠BOE=68°；③∠BOD=22°；④∠AOF=66°．正确的为（ ）
A、①②③ B、②③④ C、①②④ D、①②③④ -
13、在平面直角坐标系中，点P（2，-3）向右移动3个单位长度，再向上移动2个单位长度后的坐标是（ ）A、（5，1） B、（1，-5） C、（5，-1） D、（0，-5）
-
14、下列各点在第四象限的是（ ）A、（2，1） B、（2，-1） C、（-1，2） D、（2，0）
-
15、设=a，=b，则用含a，b的式子表示 ， 可得（ ）A、2 B、4ab C、2ab D、4
-
16、 要证明命题“若a＞b，则a2＞b2”是假命题，下列a，b的值能作为反例的是（ ）A、a=2，b=1 B、a=-2，b=-1 C、a=-1，b=-2 D、a=2，b=-1
-
17、 如图，直线 ， 直角三角板的 角顶点 A 在直线 MN 上，直角顶点 C 和另一顶点 B 在两条平行线之间. 的平分线 AD 交直线 PQ 于点 D，设 的度数为 .
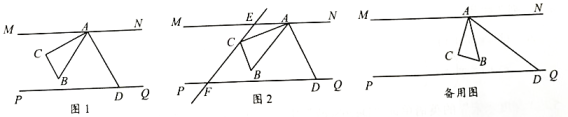(1)、 如图 1，若 ， 求 的值.(2)、 过点 C 的直线分别交 MN， PQ 于点 E， F（点 E 不与点 A 重合）.① 若 ， 如图 2，请判断 EF 与 AB 的位置关系，并说明理由.
② 若 的角平分线交直线 PQ 于点 G，求 的度数（用含 的代数式表示）.
-
18、 先阅读下面的材料，然后回答问题：
方程的解为 ， ；方程的解为 ， ；......
(1)、 根据上面的规律，猜想的解为；(2)、 利用(1)中的结论，将方程变形为的形式并求解；(3)、 解方程：. -
19、 2025年6月1日，在嵊州氧气 BAOBAO音乐节上，具有传承和创新精神的嵊州“六小笼”和杭州“六小龙”之一云深处科技公司组团出道，在音乐节中提供畅吃小笼包活动，体现了“小吃共富”的魅力.(1)、 活动现场某小笼包摊位随机每人次赠送一份小笼包，已知一份装有4个肉包和1个豆腐包的成本为1.9元，装有2个肉包和3个豆腐包的成本为1.7元，求1个肉包和1个豆腐包的成本.(2)、 作为小笼包“派送员”的机器狗需送货至距离出发点400米处的目的地，机器狗在派送中匀速运动，由于当天地面泥泞导致机器狗工作效率降低，派送速度降低为原来的.派送来回一趟所需的时间比原来多1分钟40秒，求当天机器狗的派送速度.
-
20、 先化简，再求值.(1)、 ， 其中 ， ；(2)、 ， 其中 x 是从 -1， 0， 1， 2 中选取一个合适的数.