-
1、已知点P坐标为(k-2,4-k).(1)、若点P在y轴上,求点P的坐标;(2)、若点P在第一象限,求k的取值范围
-
2、计算:.
-
3、若关于x的不等式组的解集是x>3,则m的取值范围为.
-
4、已知点O(0,0),A(2,2),点B在x轴正半轴上,且三角形AOB的面积等于3,则点B的坐标是.
-
5、比较两个数的大小:2(填“>”或“<”或“=”)
-
6、不等式≤1的最大整数解是( )A、8 B、4 C、3 D、-1
-
7、对于命题“已知2<3,那么2a<3a”,能说明它是假命题的反例是( )A、a=-2 B、a=-1 C、a= D、a=2
-
8、估计的值在( )A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间
-
9、在一次试验中,为了估算500块大小相同的试验田中海水稻的产量,通过简单随机抽样的方法抽取了50块试验田进行测产,这项抽样调查的样本容量是( )A、500块 B、50块 C、500 D、50
-
10、北京市2025年5月1日的“日出、日中、日落时刻”如下表所示:
日出时刻
日中时刻
日落时刻
05:14:14
12:11:27
19:08:41
则北京市2025年5月1日的白昼时长是( )
A、14:52:53 B、14:23:40 C、13:54:27 D、12:54:28 -
11、下列调查中,适合采用普查的是( )A、调查广东省中学生的视力情况 B、调查宇树牌某型号机器人的使用寿命 C、调查岐江河的水质情况 D、检查“神舟二十号”载人飞船零部件的质量
-
12、如图,若在象棋盘上建立平面直角坐标系,使“炮”位于点(1,2),“马”位于点(3,0),则“兵”位于点( )
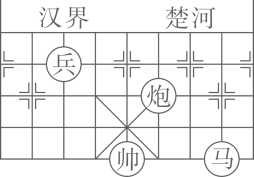 A、(2,3) B、(3,2) C、(-2,3) D、(-2,-3)
A、(2,3) B、(3,2) C、(-2,3) D、(-2,-3) -
13、如图,a//b,∠1=70°,则∠2的度数是( )
 A、110° B、100° C、80° D、70°
A、110° B、100° C、80° D、70° -
14、截至2025年5月24日24时,《哪吒之魔童闹海》全球实时票房达到158.64亿元.下图是一张哪吒图片,下列哪张图片是通过平移得到的( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
15、【背景】数学兴趣小组在学习对顶角知识时,发现若两个三角形存在对顶角的关系时,则这两个三角形的内角存在某种关系,对此数学兴趣小组展开探究。
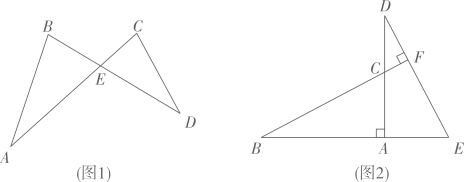 (1)、【发现】如图1,在△ABE和△DCE中,点E为AC与BD的交点。
(1)、【发现】如图1,在△ABE和△DCE中,点E为AC与BD的交点。①若∠A+∠B=100°,则∠C+∠D=;
②若∠B=∠C,则∠A与∠D之间的数量关系是;
(2)、【应用】如图2,B、A、E在同一直线上,DA⊥BE,BF⊥DE交AD于点C,BC=DE。求证:△ABC≌△ADE;
(3)、如图3,在等腰△ABC中,AB=AC,∠B=30°,D是BC边上一点,将△ABD沿AD折叠至△ADE,AB的对应边AE与BC交于点F,当△ADF为等腰三角形时,直接写出∠CDE的度数: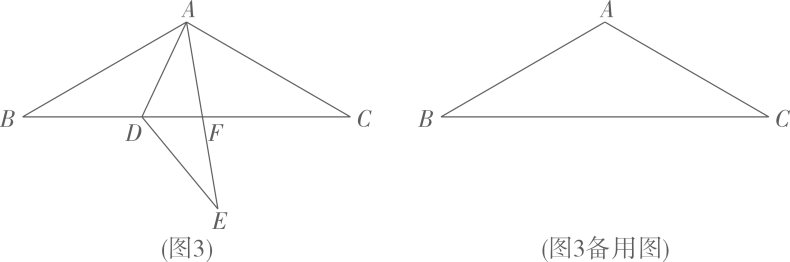 (4)、如图4,在Rt△ABC中,∠ABC=90°,BD是AC边上的高,AD=2,E是∠ABC外一点且满足∠EDC=∠EBC,BA=BE,DE=BD。记BD =x,y=S△ABD-S△BDE , 求y与x的关系式。
(4)、如图4,在Rt△ABC中,∠ABC=90°,BD是AC边上的高,AD=2,E是∠ABC外一点且满足∠EDC=∠EBC,BA=BE,DE=BD。记BD =x,y=S△ABD-S△BDE , 求y与x的关系式。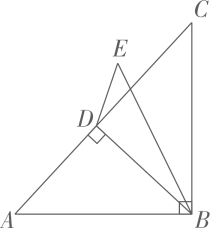
-
16、(1)、【特例感知】
已知:152=225,252=625,352=1225,·……
猜想:个位数字是5的两位数平方后,结果末尾的两个数字是25。
证明:设此两位数的十位数字是m,……
请完成上述剩余证明过程。
(2)、【类比迁移】观察下列等式:
32×38=1216;54×56=3024;79×71=5609;83×87= ▲ ;
①请写第四个等式的结果;
②数学兴趣小组发现,这若干组等式满足下列的规律:
十位数字相同、个位数字之和等于10的两个两位数相乘,可以把十位数字乘比它大1的数作为积的前两位,把个位数字的乘积作为积的后两位。”
例如

请写出一个满足此规律的一个等式: ▲ ;(不得抄写已给出的4个等式)
③设满足此规律的两个两位数中十位数字为a,其中第一个两位数的个位数字为b。请用含a、b的式子表示②中的规律,并证明其正确性。
-
17、【课本回顾】你还记得怎样用尺规作一个角等于已知角吗?你能说明其中的道理吗?小明回顾了作图过程,并进行了如下思考:

如图1,由尺规作图可知,OC=O'C',OD=O'D', ①
所以△OCD≌△O'C'D'( ② ),(填全等判定依据,如SSS,ASA,AAS,SAS)
(1)、完成上述小明思考过程中的填空;(2)、【操作应用】如图2,已知线段a和∠α,请用尺规作一个△ABC,使BC=a,AC=2a,∠BCA=∠α;
 (3)、如图3,在四边形ABCD中,AB=AD,请利用尺规在CD边上作一点E,使得△ADE≌△ABE。(保留作图痕迹,标明字母,不写作法)
(3)、如图3,在四边形ABCD中,AB=AD,请利用尺规在CD边上作一点E,使得△ADE≌△ABE。(保留作图痕迹,标明字母,不写作法)
-
18、小亮骑自行车去上学,当他以往常的速度骑行至点A处时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校。以下是他本次上学离家距离与时间的关系示意图。根据图中提供的信息回答下列问题:
 (1)、图象所表示的两个变量中,自变量是;因变量是:(2)、小亮家到学校的距离是米;本次上学途中,小亮一共骑行了米;(3)、点A的实际意义是什么?(4)、如果小亮不买书,以往常的速度去学校,从家到学校需要多少分钟?
(1)、图象所表示的两个变量中,自变量是;因变量是:(2)、小亮家到学校的距离是米;本次上学途中,小亮一共骑行了米;(3)、点A的实际意义是什么?(4)、如果小亮不买书,以往常的速度去学校,从家到学校需要多少分钟? -
19、某学校班级为表彰一周量化考核评价为优秀的同学,设制如图1的电子刮刮卡抽奖活动,评为优秀的同学获得抽奖机会一次。其中4张刮刮卡奖励内容分别为“①免作业券1张;②与好朋友同桌一天:③薯片一包;④牛奶1瓶”。抽完奖后系统自动更新出4张上述内容的刮刮卡,并把顺序打乱。
 (1)、小明同学在某周考核中评为优秀,他在刮刮卡抽奖活动中抽中“①”的概率是:(2)、通过调查发现,该班同学对“①”最感兴趣,对“③”和“④”喜好程度一样。于是,老师将抽奖方式改为转盘,并设定:①的概率是 , ②的概率是 , ③的概率为。请在图2转盘中的扇形写上“①②③④”,使得自由转动这个转盘,当它停止时,指针分别落在“①②③④”上的概率满足上述设定。(备注:转盘中扇形的圆心角均相等)
(1)、小明同学在某周考核中评为优秀,他在刮刮卡抽奖活动中抽中“①”的概率是:(2)、通过调查发现,该班同学对“①”最感兴趣,对“③”和“④”喜好程度一样。于是,老师将抽奖方式改为转盘,并设定:①的概率是 , ②的概率是 , ③的概率为。请在图2转盘中的扇形写上“①②③④”,使得自由转动这个转盘,当它停止时,指针分别落在“①②③④”上的概率满足上述设定。(备注:转盘中扇形的圆心角均相等) -
20、先化简,再求值: , 其中。