-
1、计算:(1)、2-2-2025°-(-1)2025(2)、2024×2026-20252
-
2、如图,在四边形ABCD中,AD//BC,点E在BC上且刚好落在AB垂直平分线上,点F是CD中点,EF⊥AF,已知AD=4,BE=7,则CE=.

-
3、如图、将长方形纸片ABCD沿EF折叠,点B、C分别落在点B'、C'处,B'C'与AB相交于点G,如果∠EFC=65°,则∠AGC'=度

-
4、定义一种“四位差运算”的操作:对于一个四位数(四位数字不全相同),将各位数字重新排列组成最大四位数和最小四位数(允许首位为零),用最大数减去最小数得到差。例如,对1234进行一次“四位差运算”,得4321-1234=3087,二次“四位差运算”就是把一次“四位差运算”的结果再做“四位差运算”的操作。则对初始数1234连续进行三次“四位差运算”后的结果是.
-
5、某林业部门统计某种幼树在一定条件下的移植成活率,结果如表所示:
移植总数n
400
1500
3500
7000
9000
14000
成活数m
369
1335
3203
6335
8073
12628
成活的频率
0.923
0.890
0.915
0.905
0.897
0.902
根据表中数据,估计这种幼树移植成活的概率为 (结果精确到0.1).
-
6、 如图,坪山中心广场拟开发一块新花坛,花坛如阴影部分所示。点C是线段BG上的一点,以BC,CG为边向两边作正方形,面积分别是和 , 已知 , 图中阴影部分面积为6。则( )
 A、20 B、35 C、40 D、50
A、20 B、35 C、40 D、50 -
7、如图,为测量坪山河宽度,某同学在河岸边选定观测点A和B,在岸边标记目标点C、D,使AC=CD,并利用测角仪测得∠BAC=∠EDC=90°。此时,利用三角形全等的性质,测量DE长度即可得到河宽。要说明两个三角形全等最恰当的理由是( )
 A、SSS B、ASA C、SSA D、SAS
A、SSS B、ASA C、SSA D、SAS -
8、在坪山区聚龙山湿地公园中,白鹭捕食小鱼体现捕食关系,水鸟被舌状绦虫寄生形成寄生关系,落羽杉与水生植物争夺阳光属竞争关系,而蜜蜂为荔枝树传粉、蚂蚁保护蚜虫获取蜜露,生动展现了生物间的互利共生。捕食关系、寄生关系、竞争关系和共生关系在生态学中被称为生物间的相互作用。它们可以通过不同形态的曲线来描述。其中共生关系又叫互利共生,是两种生物彼此和谐互利地生活在一起,下列选项能表示共生关系的是( )A、
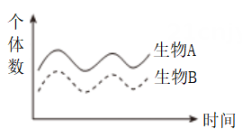 B、
B、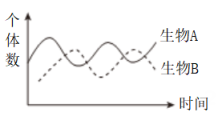 C、
C、 D、
D、
-
9、小明在坪山区中心公园沿着一条小路散步,小明两次拐弯后方向与原来相同,已知第一次拐的角∠CBD=15°,第二次拐的角∠FDE是( )
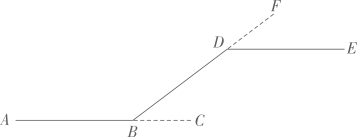 A、30° B、15° C、165° D、35°
A、30° B、15° C、165° D、35° -
10、公园中有两条近似垂直的绿道,一条长45米,一条长60米,现打算再修一条连接两条绿道端点A和B的笔直小径,则小径AB的长可能为( )
 A、15米 B、110米 C、72米 D、120 米
A、15米 B、110米 C、72米 D、120 米 -
11、以下事件中,属于必然事件的是( )A、坪山河的河水在冬季结冰 B、太阳从东边升起 C、坪山大道明天早上必堵车 D、坪山的公园数量在未来会不断减少
-
12、 新能源汽车每公里减排 0.016kg,用科学记数法表示是( )A、 B、 C、 D、
-
13、下列汉字图形中,哪些可以看成轴对称图形( )A、
 B、
B、 C、
C、 D、
D、
-
14、等腰三角形是常见的轴对称图形,某学习小组利用两个等腰三角形开展了以下研究性学习:
 (1)、如图1,△ABC和△DEF是等腰三角形,AB=AC,DE=DF,底边BC=EF.将点B、C分别和点E、F重合,得到如图2的新图形,该图形 ▲ (填“是”或“不是”)轴对称图形,如果是,请画出它的对称轴。(2)、如图3,△ABC和△AEF是两个全等的等腰三角形,两底边BC、EF相交于点G,连接BE、CF,小组成员发现一组新的全等三角形,它们是: ▲ ≌ ▲ 请说明理由,
(1)、如图1,△ABC和△DEF是等腰三角形,AB=AC,DE=DF,底边BC=EF.将点B、C分别和点E、F重合,得到如图2的新图形,该图形 ▲ (填“是”或“不是”)轴对称图形,如果是,请画出它的对称轴。(2)、如图3,△ABC和△AEF是两个全等的等腰三角形,两底边BC、EF相交于点G,连接BE、CF,小组成员发现一组新的全等三角形,它们是: ▲ ≌ ▲ 请说明理由,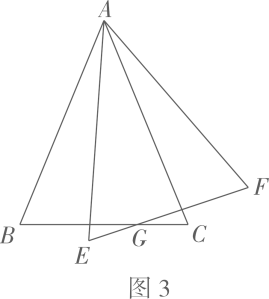 (3)、如图4,△ABC和△AEF都是等腰直角三角形,∠BAC=∠EAF=90°,连接BE、CF,延长BE分别交AC、CF于点M、N,求∠BNC的度数.
(3)、如图4,△ABC和△AEF都是等腰直角三角形,∠BAC=∠EAF=90°,连接BE、CF,延长BE分别交AC、CF于点M、N,求∠BNC的度数.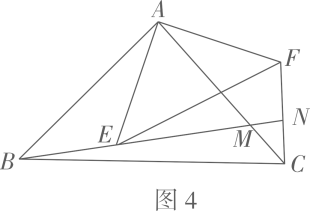
-
15、光明乳鸽是广东省深圳市的传统名菜,选用25-28天乳鸽经秘制卤水煮炸而成,皮脆肉嫩,骨香多汁,闻名遐迩,某外卖平台计划销售光明乳鸽,已知以下信息:
信息一:每只乳鸽的成本为15元,售价为30元,日销量为200只.
信息二:采用“薄利多销”的策略,若售价每降1元,日销量将增加20只.设售价为x元(x为整数,且x>15),日销量为y只,售价、日销量的关系如下表:
售价 x/元
29
28
27
26
25
日销量y/只
220
240
260
280
300
信息三:日利润=(售价-成本)×日销量.
根据以上信息,回答下列问题:
(1)、表格中反映了两个变量之间的关系,其中是自变量,是因变量;(2)、当售价x=23时,日销量为只,日利润为元;(3)、设日利润为w元,求日销量y与x的关系式以及日利润w与x的关系式. -
16、如图,在△ABC中,∠ABC=90°,以点B为圆心,以BA为半径作弧,交AC于点D,连接BD.
 (1)、请用尺规作线段CD的垂直平分线PQ(保留作图痕迹,不要求写作法):(2)、若PQ交BC于点E,连接DE,且AB=3,BC=7,求△BDE的周长.
(1)、请用尺规作线段CD的垂直平分线PQ(保留作图痕迹,不要求写作法):(2)、若PQ交BC于点E,连接DE,且AB=3,BC=7,求△BDE的周长. -
17、填空,并在括号里注明理由:
如图,在△ABC中,CD是△ABC的角平分线,点E在AC上,且DE=CE.
 (1)、试说明 BC//DE;
(1)、试说明 BC//DE;解:因为CD是△ABC的角平分线(已知),
所以∠1=∠2( )
因为 DE=CE(已知),
所以∠1=∠3( )
所以∠2= ▲ ( )
所以BC∥DE( ).
(2)、若∠A=74°,∠B=62°,直接写出∠BDC的度数.解: ∠BDC=°
-
18、某中学为了解七年级学生对课后延时服务项目的参与情况,随机抽取50名学生进行问卷调查,课后延时服务项目分为以下四类:A.艺术素养、B.体育锻炼、C.科技探究、D.作业辅导.现将调查结果整理成如下不完整的统计表:
项目
A
B
C
D
人数
15
10
5
频率
0.3
0.1
(1)、请补全统计表中的空缺数据(直接填写在表中):(2)、从参与调查的学生中随机抽取1人,抽到的学生恰好参与项目B是事件(从“随机”“必然”“不可能”选一个填入);(3)、若该校七年级共有400名学生,试估计选择项目A的学生人数. -
19、数学课上,王老师请了小深和小圳上讲台做题,以下是他们的解答过程:
(小深)计算:[(x+y2-(x-y)2] ÷2xy
解:原式=[(x2+2xy+y2)-(x2-2xy+y2)]÷2xy... ①
=(x2+2xy+y2-x2+2xy-y2)÷2xy……②
=4xy+2xy……③
=2
(小圳)先化简,再求值:
x(x+2y)-(x+1)2+2x,其中x= , y=-2025.
解:原式=x2+2xy-x2+2x+1+2x... ①
=2xy+1……②
.......
(1)、解答过程里,小深第②步的解法依据是____(填选项)·A、等式的基本性质 B、乘法交换律 C、去括号法则 D、合并同类项(2)、小圳从第 ▲ 步开始出现错误;请你写出这道题正确且完整的解答过程. -
20、计算:.