相关试卷

1、二次函数 $y_{1} = a x^{2} + b x$ (a，b为实数，a<0)的图象的对称轴为直线x=2，且经过点(m，n).若二次函数. $y_{2} =$ $a {(x - 2)}^{2} + b (x - 2)$ 的图象经过点(m-2，n)，则关于x的方程 $a {(x - 2)}^{2} + b (x - 2) = n$ 的解是 ( )

A、 $x_{1} = 2, x_{2} = 4$ B、 $x_{1} = 0, x_{2} = 2$ C、 $x_{1} = 0, x_{2} = 4$ D、 $x_{1} = 2, x_{2} = 6$

查看解析
2、在平面直角坐标系中，抛物线 $y = a x^{2} - 4 a x + 2$ 与x轴的一个交点为A(-1，0)，另一个交点为 B，则AB的长为 ( )

A、2 B、3 C、6 D、8

查看解析
3、如图是一个食品包装盒的表面展开图.

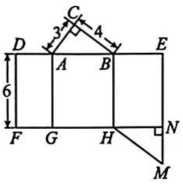(1)、请写出这个包装盒的几何体名称：；

(2)、请根据图中所标的尺寸，求这个包装盒的侧面积.

查看解析
4、走马灯，又称仙音烛，是中国特色工艺品，常见于除夕、元宵、中秋等节日.在一次综合实践活动中，一同学用如图所示的纸片，沿折痕折成一个棱锥形的“走马灯”，正方形做底，侧面有一个三角形面上写了“祥”字，当灯旋转时，正好看到“吉祥如意”的字样，则在 A，B，C面依次写上的字是( )

A、吉如意 B、意吉如 C、吉意如 D、意如吉

查看解析
5、如图，圆柱的底面直径为AB，高为AC，一只蚂蚁在C处，沿圆柱的侧面爬到 B 处，现将圆柱侧面沿 AC “剪开”，在侧面展开图上画出蚂蚁爬行的最短路线，正确的是图 K30-18中的( )

A、 B、 C、 D、

查看解析
6、如图①，一个2×2 的平台上已经放了一个棱长为1的正方体，要得到一个几何体，其主视图和左视图如图②，平台上至少还需再放这样的正方体( )

A、1个 B、2个 C、3个 D、4个

查看解析
7、如图是由 6个大小相同的小正方体搭成的几何体，当去掉某一个小正方体时，与原几何体比较，下列说法正确的是( )

A、去掉①，主视图不变 B、去掉②，俯视图不变 C、去掉③，左视图不变 D、去掉④，俯视图不变

查看解析
8、一个圆锥的母线长为6，底面半径为 2，则该圆锥的侧面积为(结果保留π).

查看解析
9、某几何体的三视图如图所示，则该几何体是图中的( )

A、 B、 C、 D、

查看解析
10、如图所示的几何体是由一个圆柱和一个长方体组成的，它的主视图是图中的( )

A、 B、 C、 D、

查看解析
11、如图所示的几何体由3个同样大小的正方体搭成，它的俯视图是图中的( )

A、 B、 C、 D、

查看解析
12、在如图所示的实物图中，主视图是长方形的是( )

A、 B、 C、 D、

查看解析
13、“绫罗尺价”问题：“今有绫、罗共三丈，各直钱八百九十六文， ▲ .”其大意为：“现在有绫布和罗布长共3丈(1丈=10尺)，已知绫布和罗布分别出售均能收入 896 文， ▲ .”设绫布有x尺，则可得方程为 $120 - \frac{896}{x} = \frac{896}{30 - x},$ 题中“ ▲ ”处表示缺失的条件，根据此情境，下列可以作为补充条件的是( )

A、每尺绫布比每尺罗布贵120文 B、每尺绫布比每尺罗布便宜120文 C、每尺绫布和每尺罗布一共需要120 文 D、绫布的总价比罗布的总价便宜120文

查看解析
14、 (2023 嘉兴、舟山)小丁和小迪分别解方程 $\frac{x}{x - 2} -$ $\frac{x - 3}{2 - x} = 1$ 的过程如下：
小丁：
解：去分母，得x-(x-3)=x-2.
去括号，得x-x+3=x-2.
合并同类项，得3=x-2，解得x=5.
∴原方程的解是x=5.
小迪：
解：去分母，得x+(x-3)=1.
去括号，得x+x-3=1.
合并同类项，得2x-3=1，解得x=2.
经检验，x=2是方程的增根，原方程无解.
你认为小丁和小迪的解法是否正确?若正确，请在框内打“✔”；若错误，请在框内打“×”，并写出你的解答过程.

查看解析
15、若关于x的分式方程 $\frac{m x + 1}{x - 2} = 1$ 有增根，则m的值是( )

A、 $- \frac{1}{2}$ B、1 C、 $- \frac{1}{2}$ 或0 D、0或1

查看解析
16、为进一步深入开展“五水共治”工作，提升水环境质量，某工程队承担了3000米河道的清淤任务，为了减少施工对居民生活的影响，实际施工时每天的工作效率比原计划增加了20%，结果提前10天完成这一任务.设原计划每天完成x米的清淤任务，则所列出的方程正确的是( )

A、 $\frac{3000}{x} + 10 = \frac{3000}{(1 - 20 %) x}$ B、 $\frac{3000}{x} + 10 = \frac{3000}{(1 + 20 %) x}$ C、 $\frac{3000}{x} - 10 = \frac{3000}{(1 - 20 %) x}$ D、 $\frac{3000}{x} - 10 = \frac{3000}{(1 + 20 %) x}$

查看解析
17、综合与探究
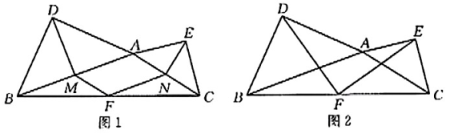
【问题情境】在△ABC中，分别以AB和AC为边向外作等腰直角三角形ABD和等腰直角三角形ACE，其中∠ADB=∠AEC=90°，AD=BD，AE=CE，F是边BC的中点.
【猜想验证】

(1)、如图1，若DM丄AB，ENLAC，垂足分别是M，N，连接MF，NF.试判断四边形AM-FN的形状，并说明理由。

(2)、【深入探究】
如图2，连接DF，EF.
①试判断线段DF与EF的数量关系和位置关系，并说明理由，
②若DF= $\sqrt{2}$ ，求四边形ADBC和△ACE的面积之和.

查看解析
18、综合与实践
【项目背景】在数字化农业快速发展的时代，大数据分析与智能决策在水果产业中的作用愈发关键，芒果作为深受消费者喜爱的热带水果，其市场需求持续增长，为提升芒果产业的整体效益，实现精准化种植与科学化管理，某农业科技研究小组针对2024年n个芒果主产区的产量数据展开深入研究，通过对这些数据的专业分析，为芒果种植园的规划布局、采摘时间安排、仓储保鲜策略及市场销售渠道拓展提供有力的数据支撑，借助科技力量优化芒果产业的全产业链环节.
【数据收集与整理】将收集的n个芒果主产区的产量（产量记为x，单位：万吨）数据进行如下分组：
组别
A
B
C
D
E
x/万吨
30≤x<40
40≤x<50
50≤x<60
60≤x<70
70≤x<80
整理数据后得到部分信息如下：
①C组的数据（单位：万吨）为51，56，56，54，55，58.
②2024年芒果主产区产量的频数分布直方图和扇形统计图如图所示.
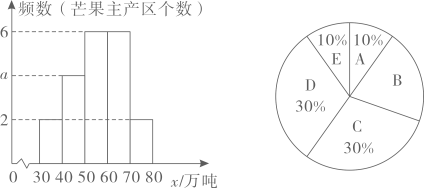
（任务1）n=    ▲         ， a=    ▲        .
【数据分析与运用】（任务2）C组数据的众数是    ▲        、收集的这n个芒果主产区2024年芒果产量的中位数是    ▲        .
（任务3）2024年各组芒果的平均产量如下表：
组别
A
B
C
D
E
平均产量/万吨
35
43
55
68
74
求这n个芒果主产区2024年芒果的平均产量.
（任务4）下列结论正确的是    ▲        （填序号）.
①如果收集的n个芒果主产区的产量数据都增加0.5万吨，那么这些地区芒果产量的总数
会增加0.5万吨.
②如果A组的所有数据都增加5万吨，那么这n个芒果主产区芒果产量的平均数会增加0.5万吨.
③如果各地区芒果产量数据的最大值与最小值相差40万吨，且最低产量在A组，那么最高产量一定在E组.

查看解析
19、如图，直线 $l : y = \sqrt{3} x + \sqrt{3}$ 与x轴、y轴分别交于B，A两点，M为线段AB的中点.

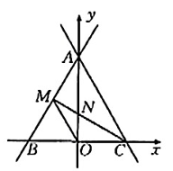(1)、求点A，B，M的坐标.

(2)、直线l关于y轴对称的直线为 $l^{^{'}}$ ，直线 $l^{^{'}}$ 交x轴于点C，求直线 $l^{^{'}}$ 的解析式.

(3)、在（2）的条件下，直线MC与y轴的交点为N，连接OM，求 $\frac{O M}{O N}$ 的值.

查看解析
20、如图，在□ABCD中，BE⊥AD，交DA的延长线于点E，AE=AD.

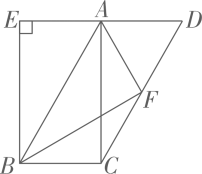(1)、求证：四边形AEBC是矩形.

(2)、F为CD的中点，连接AF，BF.已知AB=6，BF⊥AF，求BF的长.

查看解析

上一页 421 422 423 424 425 下一页跳转

组别	A	B	C	D	E
x/万吨	30≤x<40	40≤x<50	50≤x<60	60≤x<70	70≤x<80

组别	A	B	C	D	E
平均产量/万吨	35	43	55	68	74