-
1、综合与实践:探索机器狗的速度问题.
素材1:图1是某款机器狗,它的最快速度(米/秒)与总质量(千克)(包括所载物体的质量)的部分数据如表,在直角坐标系中画出对应点,并用光滑曲线连起来(图2).

总质量千克
60
80
90
100
120
最快速度米秒
6
4.5
4
3.6
3
素材2:机器狗自身质量为60千克,实验室距离试验点540米,机器狗需从试验点出发,送12千克设备到实验室,卸下设备后马上原路返回.(装卸设备时间忽略不计)经探究发现是的正比例函数、一次函数、反比例函数中的一种.
任务1:判断是的哪种函数类型,并求出该函数表达式.
任务2:求机器狗所用的最短时间.
-
2、已知一元二次方程 .(1)、若方程的一个根为2,求的值.(2)、当时,求证:方程有两个实数根.
-
3、尺规作图:在矩形中,要求用直尺和圆规作菱形 , 使点分别在边上.

小明:如图1,作的中垂线分别交于点 , 连结 .
小刚:如图2,连结 , 作的中垂线分别交于点 , 连结 .
请选择一位同学的作法,判断是否正确,并说明理由.(注:若全选,按第一种作答评分)
-
4、某校举行班容班貌评比活动,以班级为单位,评比项目包括文化卫生、板报宣传和特色栏目.三个班级各项目得分如下表(单位:分)所示:
项目
班级
文化卫生
板报宣传
特色栏目
班
92
88
93
班
94
93
89
班
89
94
96
(1)、已知两班的平均分分别是91分、92分,通过计算指出哪个班级平均分最高.(2)、若将文化卫生、板报宣传和特色栏目的得分按的比例计算总成绩,此时班的总成绩分别为分和分,求班的总成绩,并根据总成绩从高到低给出班级排名. -
5、如图,为四边形的对角线,已知 .
 (1)、求证:四边形是平行四边形.(2)、分别为的中点,连结 . 若 , 求的长.
(1)、求证:四边形是平行四边形.(2)、分别为的中点,连结 . 若 , 求的长. -
6、(1)计算: .
(2)解方程: .
-
7、如图,矩形的顶点在轴正半轴上,A为的中点,反比例函数(为常数,)的图象经过点 , 交于点 . 若与的面积之和为4,则的值为 .

-
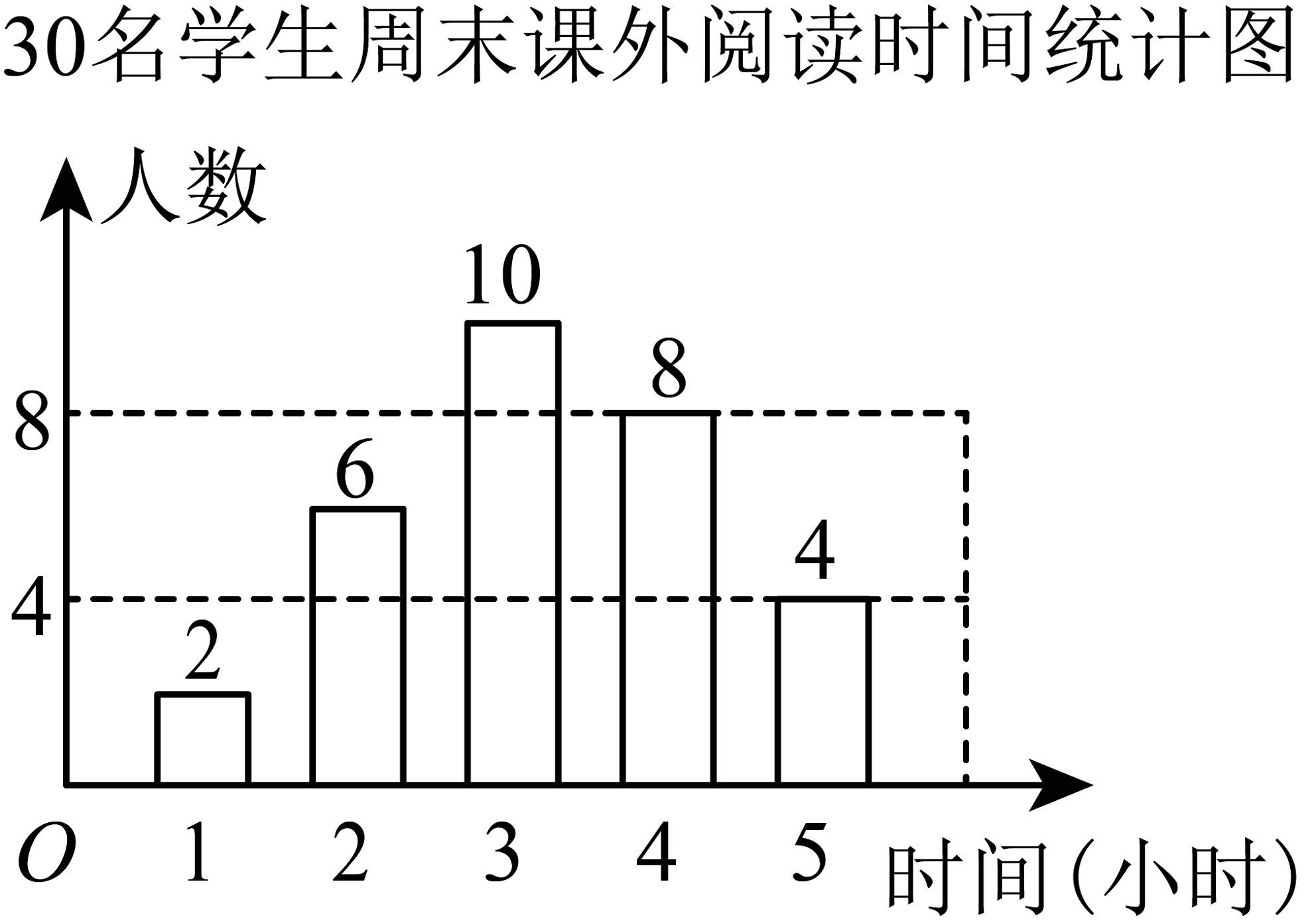
8、每年4月23日是世界读书日,某校为了解学生周末课外阅读情况,随机抽取了30名学生,得到统计图如图所示,则该30名学生周末课外阅读时间的众数为小时.
-
9、小马同学在解方程时,等号左边的一个数字不小心被墨水污染了,如右式:
 . 已知一个根 , 则另一个根 .
. 已知一个根 , 则另一个根 . -
10、计算: .
-
11、如图,点在线段上,射线 , 连结 , 以为邻边作 , 连结 , 记的长为的长为 . 若 , , , 则在点的运动过程中,下列代数式的值不变的是( )
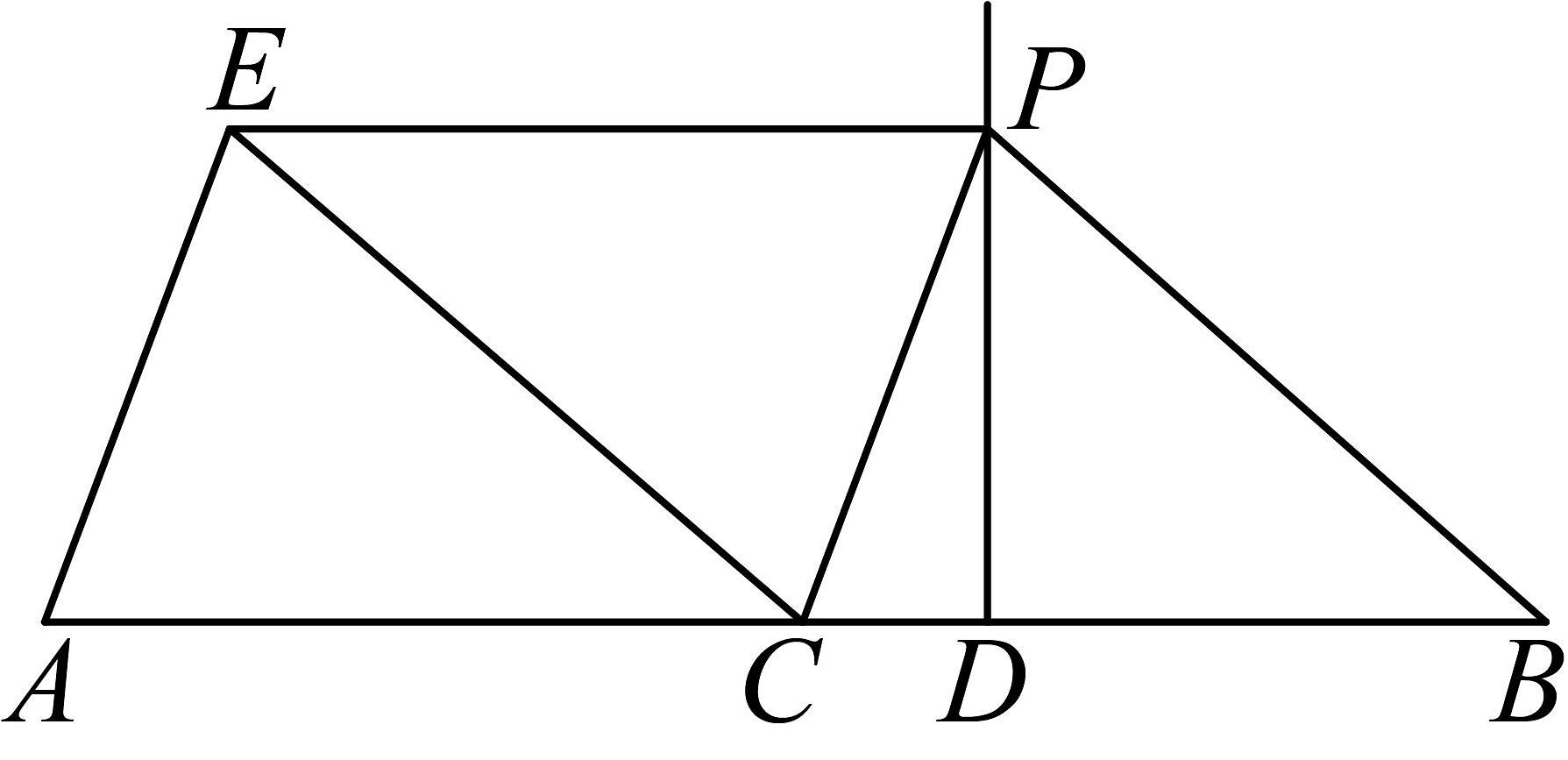 A、 B、 C、 D、
A、 B、 C、 D、 -
12、王老师设计了接力游戏:每人只能看到前一人的方程,并继续进行变形,将结果传递给下一人,最终求出方程的解,过程如图所示.
上述求解过程中,错误的是( )
A、甲 B、乙 C、丙 D、丁 -
13、温州市2022年(国内生产总值)约为8030亿元,2024年约为9719亿元.设这两年温州市的平均增长率为 , 则可列出方程( )A、 B、 C、 D、
-
14、若算式的结果是有理数,则※表示的运算符号是( )A、 B、 C、 D、
-
15、若点都在反比例函数的图象上,则下列判断正确的是( )A、 B、 C、 D、
-
16、用反证法证明命题“在中,如果 , 那么”时,应假设( )A、 B、 C、 D、
-
17、如图,在菱形中,交于点 . 若 , 则的长为( )
 A、5 B、6 C、8 D、10
A、5 B、6 C、8 D、10 -
18、下列四个人工智能的图标中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
19、小明作业本中有一页被墨水污染了,已知他所列的方程组是正确的,写出题中被墨水污染的条件,并求解这道应用题.
应用题:小东在某商场中看中的一台电视和一台空调在“五一”前共需要5500元.由于该商场开展“五一”促销活动,同样的电视打八折销售,
 ,于是小东在促销期间购买了同样的电视一台.空调两台,共花费7200元.求“五一”前同样的电视和空调每台各多少元?
,于是小东在促销期间购买了同样的电视一台.空调两台,共花费7200元.求“五一”前同样的电视和空调每台各多少元?解:设“五一”前同样的电视每台x元,空调每台y元,根据题意,得

-
20、如图,直线与直线相交于点 , 与轴分别交于两点.
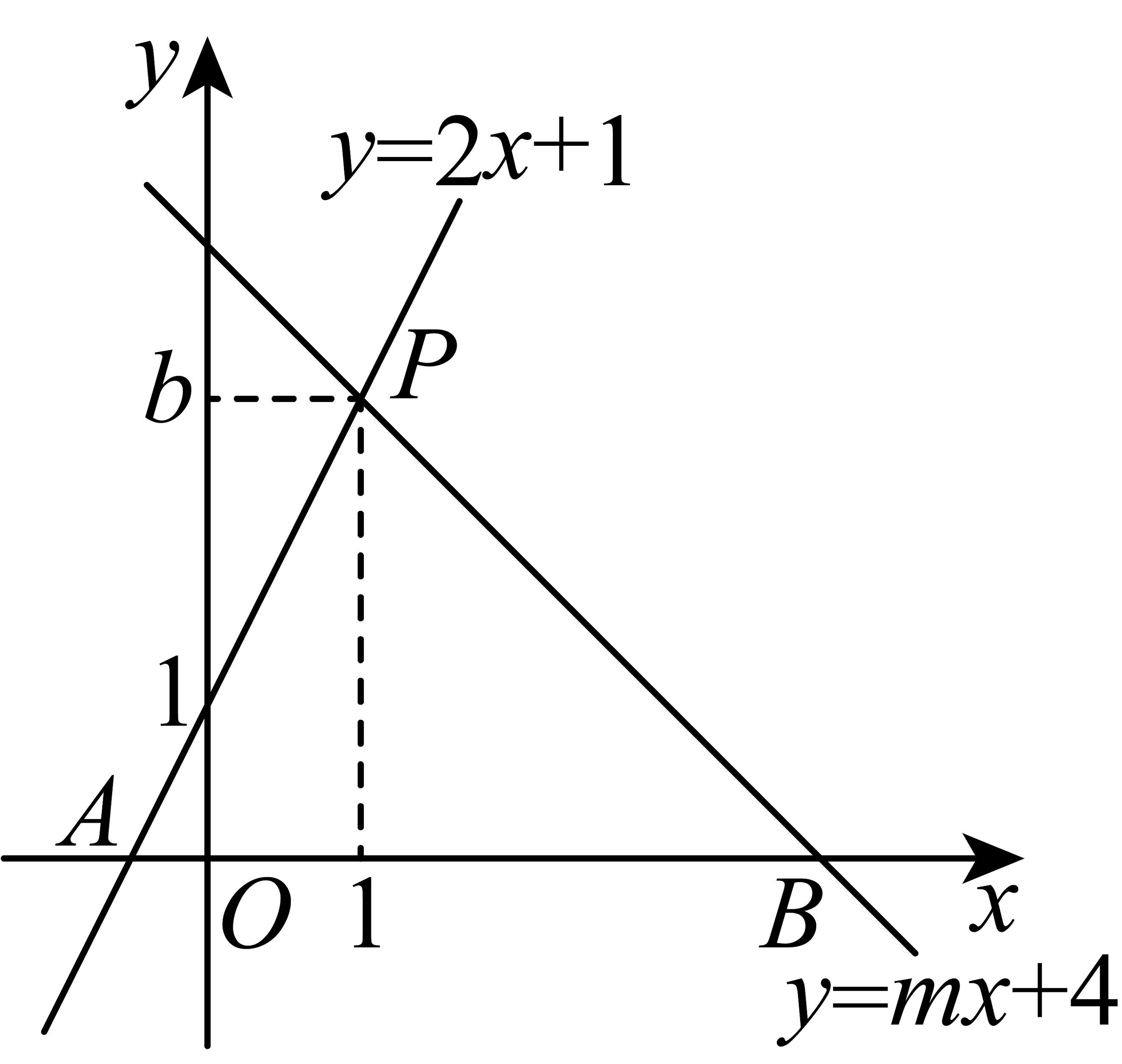 (1)、求的值,并结合图象写出关于的方程组的解;(2)、根据图象,直接写出关于的不等式的解集;(3)、求的面积.
(1)、求的值,并结合图象写出关于的方程组的解;(2)、根据图象,直接写出关于的不等式的解集;(3)、求的面积.