-
1、甲、乙两位同学将两张全等的直角三角形纸片进行裁剪和拼接,尝试拼成一个尽可能大的正方形.
要求:①直角三角形纸片的两条直角边长分别为30cm和40cm;
②在两张直角三角形纸片中各裁剪出一个图形,使它们的形状和大小都相同;
③将这两个图形无缝隙地拼成一个正方形,正方形的边长尽可能大.
甲同学的方案

乙同学的方案

请根据以上信息,回答下列问题:
(1)、计算甲、乙两位同学方案中拼成的正方形的边长,并比较大小;(2)、请设计一个方案,使拼成的正方形的边长比甲、乙两位同学拼成的正方形的边长都大.(方案要求:请在图的两个直角三角形中分别画出裁剪线,标出所有裁剪线的长,求出这个正方形的边长)
-
2、用某型号拖把去拖沙发底部地面的截面示意图如图所示,拖把头为矩形ABCD,AB=16cm,DA=2cm.该沙发与地面的空隙为矩形EFGH,EF=55cm,HE=12cm.拖把杆为线段OM,长为45cm,O为DC的中点,OM与DC所成角α的可变范围是14°≤α≤90°,当α大小固定时,若OM经过点G,或点A与点E重合,则此时AF的长即为沙发底部可拖最大深度.
 (1)、如图①,当α=30°时,求沙发底部可拖最大深度 AF的长;(结果保留根号)(2)、如图②,为了能将沙发底部地面拖干净,将α减小到14°,请通过计算,判断此时沙发底部可拖最大深度 AF 的长能否达到55cm.(参考数据: 0.97, tan 14°≈0.25)
(1)、如图①,当α=30°时,求沙发底部可拖最大深度 AF的长;(结果保留根号)(2)、如图②,为了能将沙发底部地面拖干净,将α减小到14°,请通过计算,判断此时沙发底部可拖最大深度 AF 的长能否达到55cm.(参考数据: 0.97, tan 14°≈0.25) -
3、某校为增强学生身体素质,开展了为期一个月的跳绳系列活动.为了解本次系列活动的效果,校体育组在活动之前随机抽取部分九年级学生进行了一分钟跳绳测试,根据一定的标准将测得的跳绳次数分成A,B,C,D,E五个等级,五个等级的赋分依次为10分、9分、8分、7分、6分,将测试结果整理后,绘制了统计图如图①.跳绳系列活动结束后,体育组再次对这部分学生进行跳绳测试,以相同标准进行分级和赋分,整理后绘制了统计图如图②.

请根据以上信息,回答下列问题:
(1)、求抽取的九年级学生人数,并补全图②中的统计图;(2)、若全校600名九年级学生全部参加了跳绳活动及一分钟跳绳测试,测试分级和赋分标准不变.请通过计算,估计这600名学生在跳绳活动结束后的测试中,得分不低于9分的有多少人;(3)、选择一个适当的统计量,对该校跳绳系列活动的效果进行合理评价. -
4、台灯的亮度控制可以通过用旋钮调节电阻控制电流的变化来实现.如图是通过该台灯的电流I(A)与电阻R(Ω)的关系图象,该图象经过点 P(440,0.5).
 (1)、求Ⅰ关于R的函数表达式;(2)、当880Ω<R<1000Ω时,求Ⅰ的取值范围.
(1)、求Ⅰ关于R的函数表达式;(2)、当880Ω<R<1000Ω时,求Ⅰ的取值范围. -
5、如图,在△ABC中,∠C=50°,将AB沿射线BC的方向平移至A'B'的位置,使B'为BC的中点,连结AA',记A'B'与AC的交点为O.
 (1)、求证:△AOA'≌△COB';(2)、若AC平分∠BAA',求∠B的度数.
(1)、求证:△AOA'≌△COB';(2)、若AC平分∠BAA',求∠B的度数. -
6、 【知识链接】
对于三角形中的重要结论“在同一个三角形中,等边对等角”,我们可以构造全等三角形来证明.如图1,在中,已知 , 可证 , 蛟蛟同学的证法是:作的角平分线交于点 , 则 , 通过“边角边”证明 , 则 . 请你利用该结论继续探究:
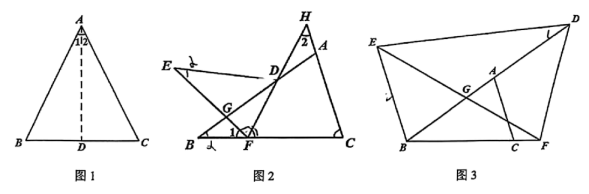 (1)、【初步应用】
(1)、【初步应用】在中,若 , , 则°.
(2)、【破茧启思】如图2,在中, , 点在上,点在上,延长线与延长线交于点是外一点,与交于点 , 若 , .
① ▲ . (用含的代数式表示)
②若 , 求 .
(3)、【攀登高峰】如图3,在中, , 点、分别在、延长线上,是外一点,与交于点 , 若 , 试探究的数量关系并证明.
-
7、 阅读下列材料:我们把形如的式子称为“行列式”,其运算法则为: . 例如: . 请你运用材料回答:(1)、计算: .(2)、已知 , 求的值.(3)、若的三边长为 , 满足 , , 求的周长.
-
8、 2025年春晚《秧BOT》节目中的机器人舞蹈,体现了我国人工智能领域的飞速发展.某物流公司采用、型机器人打包物品,某天共有11个机器人运作,型机器人共打包1080件物品,型机器人共打包750件物品,已知型机器人比型机器人每天多打包30件物品.(1)、一个、型机器人每天分别打包多少件物品?(2)、“618”期间,物流公司每天使用、型机器人共同完成2460件物品的打包,请你求出所有的安排方案.
-
9、 为响应国家“体重管理年”政策,某校要了解七年级学生的课外锻炼情况,随机选取某班学生进行“最喜欢的一项体育运动”调查,并根据统计数据绘制了如下统计图,请解答:
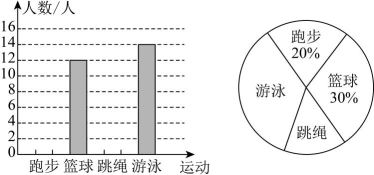 (1)、请你补全条形统计图.(2)、该校共对名学生进行了调查,在扇形统计图中,“跳绳”对应的圆心角为度.(3)、若该校七年级共有600名学生,请你估计七年级学生中最喜欢游泳运动的人数.
(1)、请你补全条形统计图.(2)、该校共对名学生进行了调查,在扇形统计图中,“跳绳”对应的圆心角为度.(3)、若该校七年级共有600名学生,请你估计七年级学生中最喜欢游泳运动的人数. -
10、 先化简 , 再从 , 3,4中选取一个合适的数作为的值代入求值.
-
11、(1)、计算: .(2)、解二元一次方程组: .
-
12、 如图,在中, , , 为射线上一动点,连结 , 将绕点顺时针旋转至交直线于点 , 若 , 则 .
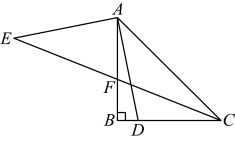
-
13、 已知关于、的方程组的解为 , 则关于、的方程组的解为 .
-
14、 若关于的分式方程有增根,则的值是 .
-
15、 如图,的三条角平分线交于点 , , 若的周长为10, , 则 .
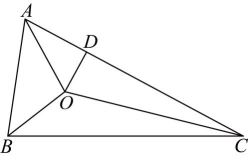
-
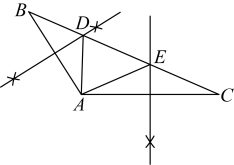
16、 如图,在中,某同学用尺规作图的方法在上作出、点,若 , , 则的周长为 .
-
17、已知 , 则 .
-
18、 因式分解:
-
19、 使分式在实数范围内有意义,则的取值范围是 .
-
20、 在长方形中, , 有三张边长分别为的正方形纸片 , 蛟蛟将纸片按图①方式放置,发现其中未被纸片覆盖的阴影部分周长为 , 川川将纸片按图②方式放置,发现其中未被纸片覆盖的阴影部分周长为 , 则( )
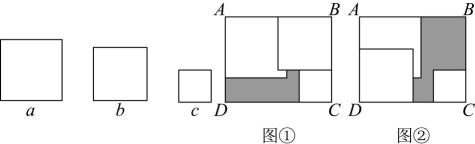 A、2 B、 C、 D、
A、2 B、 C、 D、