相关试卷
- 2017-2018学年北师大版数学八年级下册同步训练:6.4 多边形的内角和与外角和
- 2017-2018学年北师大版数学八年级下册同步训练:6.3 三角形的中位线
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.2 平行四边形的判定 ——用对角线的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.1 平行四边形的判定——用边的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.4分式方程课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.4 分式方程课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时1
-
1、【问题背景】如图1,已知是等腰三角形, , 为边BC上一动点,由点向运动,以点为圆心,为半径作半圆弧分别交于点 .
【数学思考】(1)求证:在点运动过程中,始终有;
(2)如图2,在点运动过程中,设为线段的中点,连接交半圆弧于点 , 当点H恰为的中点时,求此时线段OB的长度;
【拓展探索】(3)如图3,点在点与点重合时停止运动,若此时半圆弧与等腰三角形的腰交于另一点P,且四边形为等腰梯形,求等腰三角形顶角度数的取值范围.

-
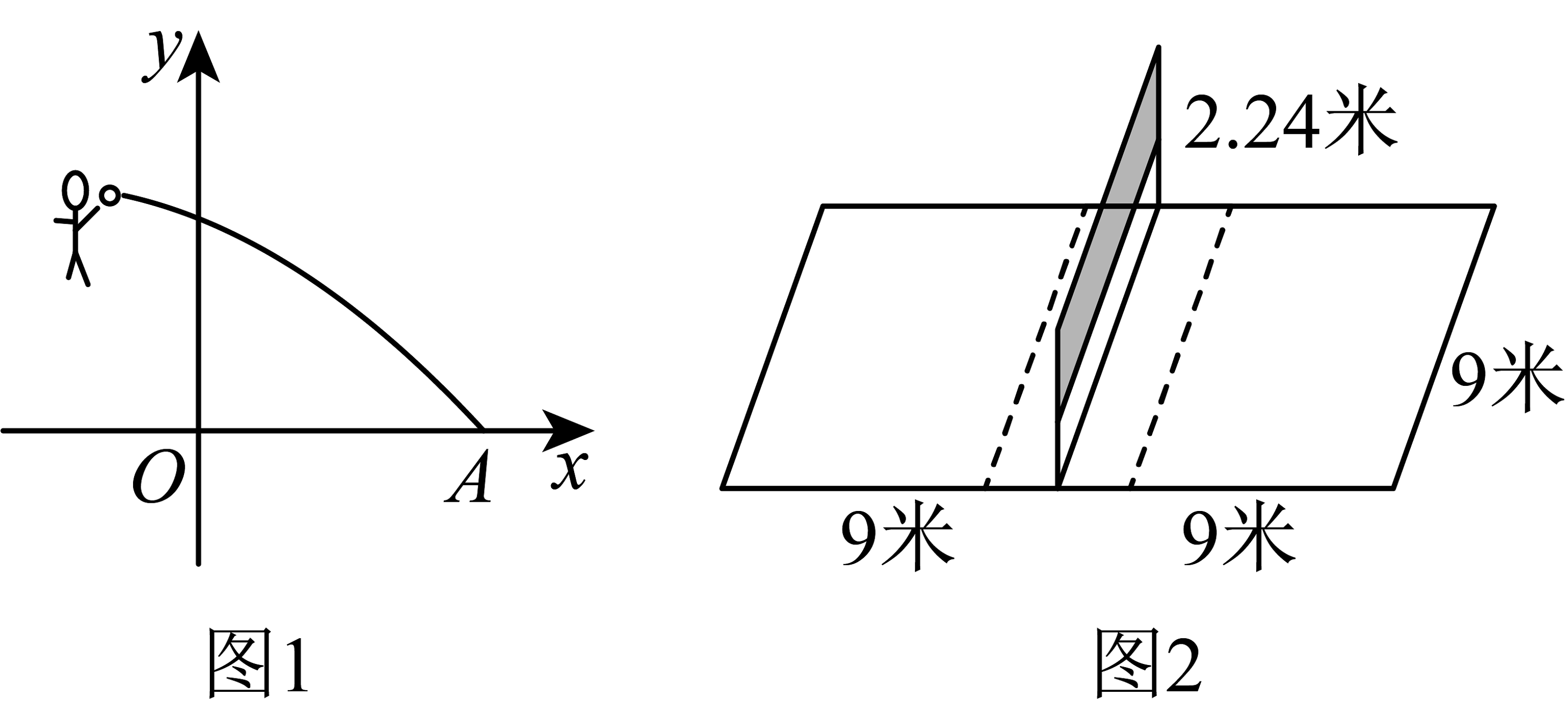
2、综合与实践.
【主题】排球运动的数学建模.
【素材】①如图1,一名排球运动员在比赛中起跳扣球,球在出手后的飞行路线可以用函数刻画,其中y轴是球网所在的位置,x轴是水平地面,排球飞行的水平距离x(米)与其飞行的高度y(米)的变化规律如下表:
x
-2
0
…
y
3
2.92
…
②如图2所示,排球场地标准:长18米,宽9米,球网高度为2.24米.
【模型建立】(1)求素材①中函数的解析式及排球的落点A的坐标;
【模拟计算】(2)若在素材①中对方运动员在球网另一侧截击,假设截击后球的轨迹与原来轨迹关于过截击点平行于y轴的直线对称,求使排球刚好能过网的截击点到球网的距离.(结果保留根号)
-
3、【阅读材料】给出如下定义:在平面直角坐标系中,点的纵坐标与横坐标的差“”称为点的“纵横差”.在某范围内某函数图象上所有点的“纵横差”中的最大值称为该范围内函数的“纵横极差”.例如:点的“纵横差”为;函数图象上所有点的“纵横差”可以表示为;当时,的最大值为 , 所以函数()的“纵横极差”为 .
【问题解决】根据阅读材料中的定义,解答下列问题:
(1)、求点的“纵横差”;(2)、求函数的“纵横极差”;(3)、若为实数,函数的“纵横极差”为 , 求的值. -
4、春日风光好,植绿正当时.为推进绿美广东生态建设,工作人员测量了5棵芒果树树苗和5棵细叶榕树苗的生长情况,数据如下:(单位:)
编号
1
2
3
4
5
芒果树
350
355
360
365
370
细叶榕
340
350
350
350
360
根据以上信息,解决下列问题.
(1)、芒果树高度的平均数为 , 细叶榕高度的平均数为;(2)、计算两种树苗高度的方差,并据此说明哪一种树苗生长更稳定. -
5、如图,已知在中 .
 (1)、实践与操作:用尺规作图法在边上找一点 , 连接 , 使得;(保留作图痕迹,不写作法,不用证明)(2)、应用与求解:若为边上的中线,且 , , 的周长为 , 求的周长.
(1)、实践与操作:用尺规作图法在边上找一点 , 连接 , 使得;(保留作图痕迹,不写作法,不用证明)(2)、应用与求解:若为边上的中线,且 , , 的周长为 , 求的周长. -
6、计算: .
-
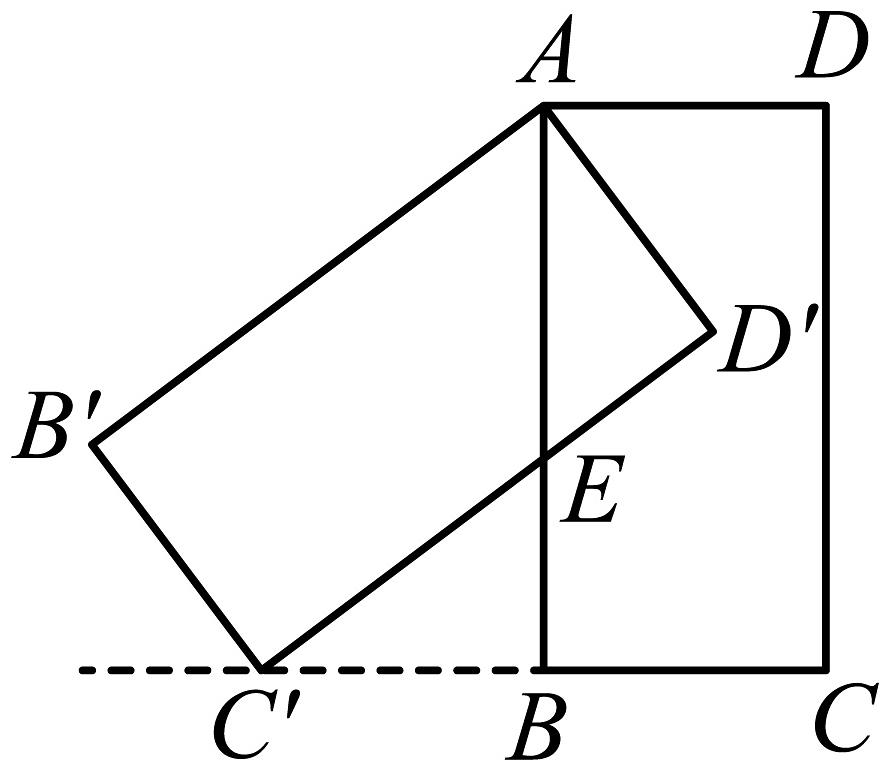
7、如图,在矩形中, , , 将矩形绕点顺时针旋转,得到矩形 , 边交于点 , 当点的对应点恰好落在线段的延长线上时,的长是 .
-
8、根据国家统计局公布的数据,2022年全国粮食总产量为13731亿斤,2024年全国粮食总产量为14130亿斤.若这两年全国粮食总产量的年平均增长率为x,则可列方程为 .
-
9、2025年3月12日是我国的第47个植树节.某校九年级8个班级春季植树的数量(单位:棵)分别为:100,120,100,120,90,120,60,70,则这8个班级植树棵数的中位数为 .
-
10、比较大小:(填“”“”或“”).
-
11、在使用某生成式人工智能生成文本时,系统为一个不完整句子末尾的四个待选词语分配了如下被选择的概率:学习、方式、方法、深度 , 那么最有可能被选择的词语是( )A、学习 B、方式 C、方法 D、深度
-
12、对于分式 , 当都扩大到原来的2倍时,则分式的值( )A、不变 B、扩大到原来的2倍 C、扩大到原来的4倍 D、不能确定
-
13、下列计算正确的是( )A、 B、 C、 D、
-
14、多项式的次数是( )A、5 B、3 C、2 D、1
-
15、的倒数是( )A、 B、3 C、0.3 D、
-
16、如图,在平面直角坐标系中,直线:交轴正半轴于点 , 交轴正半轴于点 , 直线过点
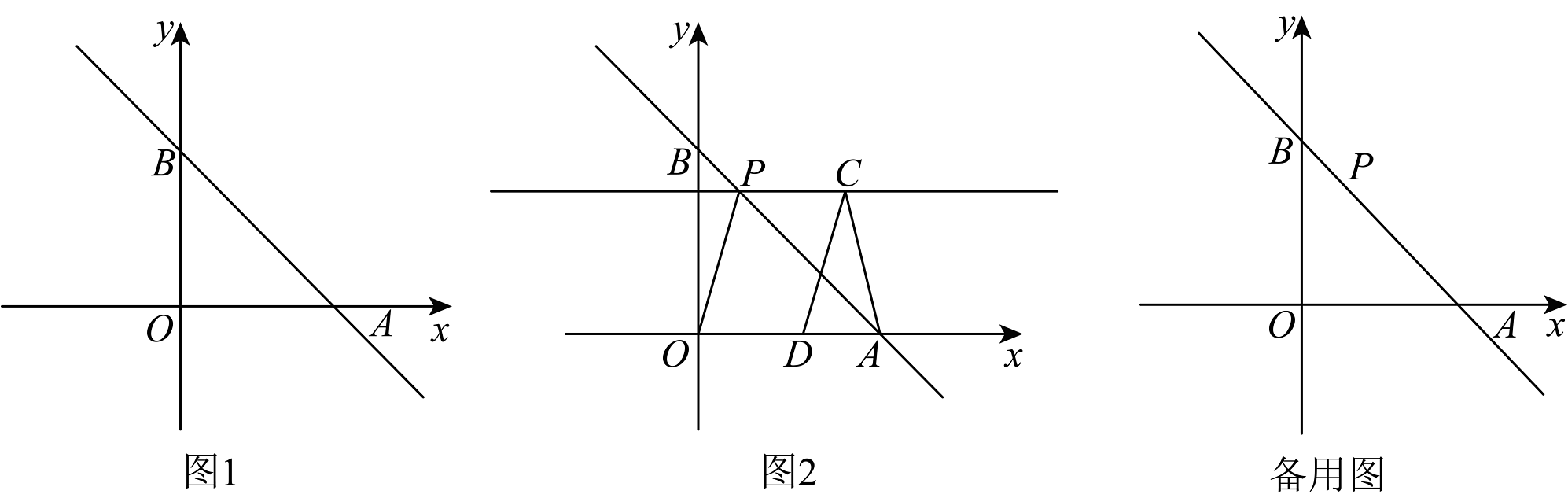 (1)、求直线解析式;(2)、连接 , 将线段沿轴正方向平移到
(1)、求直线解析式;(2)、连接 , 将线段沿轴正方向平移到①若 , 求满足条件的点的坐标;
②在平移过程中,是否存在点使得为等腰三角形,若存在,请画出图形并求出点平移的距离,若不存在,请说明理由.
-
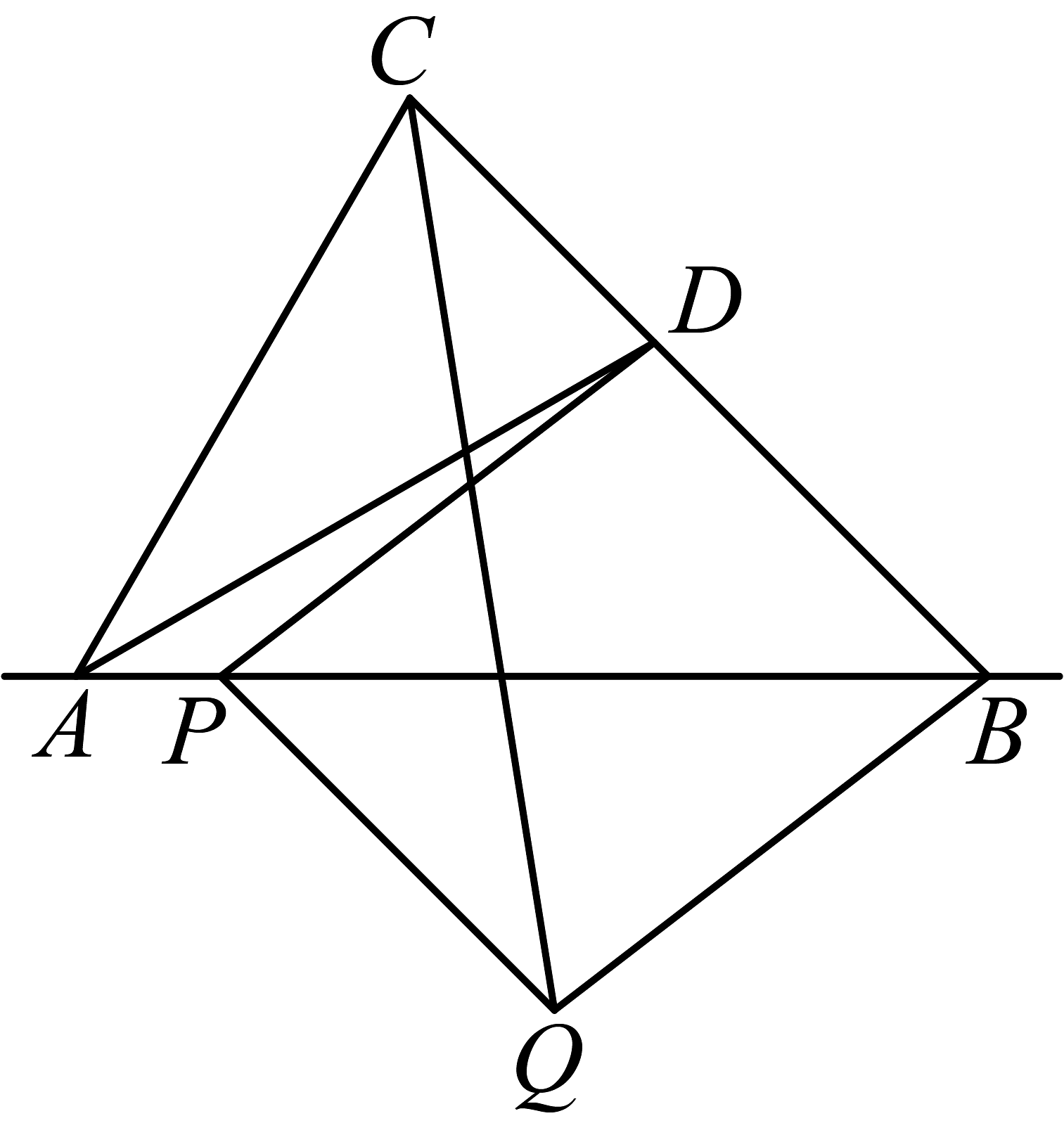
17、如图,在平分交于点D,则的长为 , 若P为直线上一动点,以为邻边构造平行四边形 , 连接 , 则的最小值为 .
-
18、定义:对于实数 , 表示 , 两数中较小的数,如 , 若关于的函数 , 且 , 则的取值范围是 .
-
19、如图,两个含角的三角尺的腰长为 . 两三角尺的斜边在同一条直线上,固定一个三角尺,另一个三角尺沿斜边平移,平移后重叠部分 , 则阴影部分的面积为 .

-
20、关于的不等式组恰有两个整数解.则实数的取值范围为