相关试卷
- 2017-2018学年北师大版数学八年级下册同步训练:6.4 多边形的内角和与外角和
- 2017-2018学年北师大版数学八年级下册同步训练:6.3 三角形的中位线
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.2 平行四边形的判定 ——用对角线的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.1 平行四边形的判定——用边的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.4分式方程课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.4 分式方程课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时1
-
1、如图1,为锐角的中线,延长与的外接圆交于点 , 点在上,连结 , , , , .
 (1)、求证:四边形为平行四边形;(2)、如图2,连结 , 若 , 求证:为等腰三角形;(3)、如图3,在(2)的条件下,连结 , 若平分 , 求的值.
(1)、求证:四边形为平行四边形;(2)、如图2,连结 , 若 , 求证:为等腰三角形;(3)、如图3,在(2)的条件下,连结 , 若平分 , 求的值. -
2、在平面直角坐标系中,为坐标原点,抛物线的顶点为 , 且与轴交于点 .(1)、求点的坐标(用含的代数式表示).(2)、若点的纵坐标为 , 求的最小值.(3)、当 , 为锐角时,求的取值范围.
-
3、某校组织学生从学校出发,乘坐大巴前往基地进行活动.大巴出发1小时后,学校因事派人乘坐轿车沿相同路线追赶.已知轿车出发2小时后追上大巴,此时两车与学校相距150千米,如图,、分别表示大巴、轿车离开学校的路程(千米)与大巴行驶的时间(小时)的函数图象.
 (1)、大巴的速度为___________千米/时.(2)、求所在直线的函数解析式.(3)、求轿车出发多长时间后,轿车与大巴首次相距5千米.
(1)、大巴的速度为___________千米/时.(2)、求所在直线的函数解析式.(3)、求轿车出发多长时间后,轿车与大巴首次相距5千米. -
4、如图,在矩形中, , 为对角线.
 (1)、尺规作图:作菱形 , 使点 , 分别在边 , 上(保留作图痕迹,不写作法).(2)、在(1)的条件下,若 , , 求的长.
(1)、尺规作图:作菱形 , 使点 , 分别在边 , 上(保留作图痕迹,不写作法).(2)、在(1)的条件下,若 , , 求的长. -
5、近年来,研学旅行作为一种寓教于乐的教学方式多次被写入国家级政策文件.某校学生会负责该校学生的一次研学活动,为设计出同学们最感兴趣的研学路线,随机抽取了部分学生进行问卷调查,并将调查结果绘制成如下不完整的统计图.
调查问卷
1.你最感兴趣的研学类型是__________(单选)
A.研学+历史 B.研学+科学 C.研学+艺术
D.研学+农业 E.研半+外文 F.研学+工业
 (1)、请补全条形统计图,并写出扇形统计图中的百分比;(2)、“”与“”所在的扇形圆心角的度数和为_______°;(3)、若该校共有4500名学生,请你估计该校对“研学+历史”最感兴趣的学生人数.
(1)、请补全条形统计图,并写出扇形统计图中的百分比;(2)、“”与“”所在的扇形圆心角的度数和为_______°;(3)、若该校共有4500名学生,请你估计该校对“研学+历史”最感兴趣的学生人数. -
6、如图,在中, , , 是边上的中线, , , 垂足为 .
 (1)、求的值.(2)、求的长.
(1)、求的值.(2)、求的长. -
7、先化简,再求值: , 其中 .
-
8、计算: .
-
9、如图,在平行四边形中,为对角线上一点, , 将沿折叠,点的对应点刚好落在边上,则与平行四边形的面积之比为 .

-
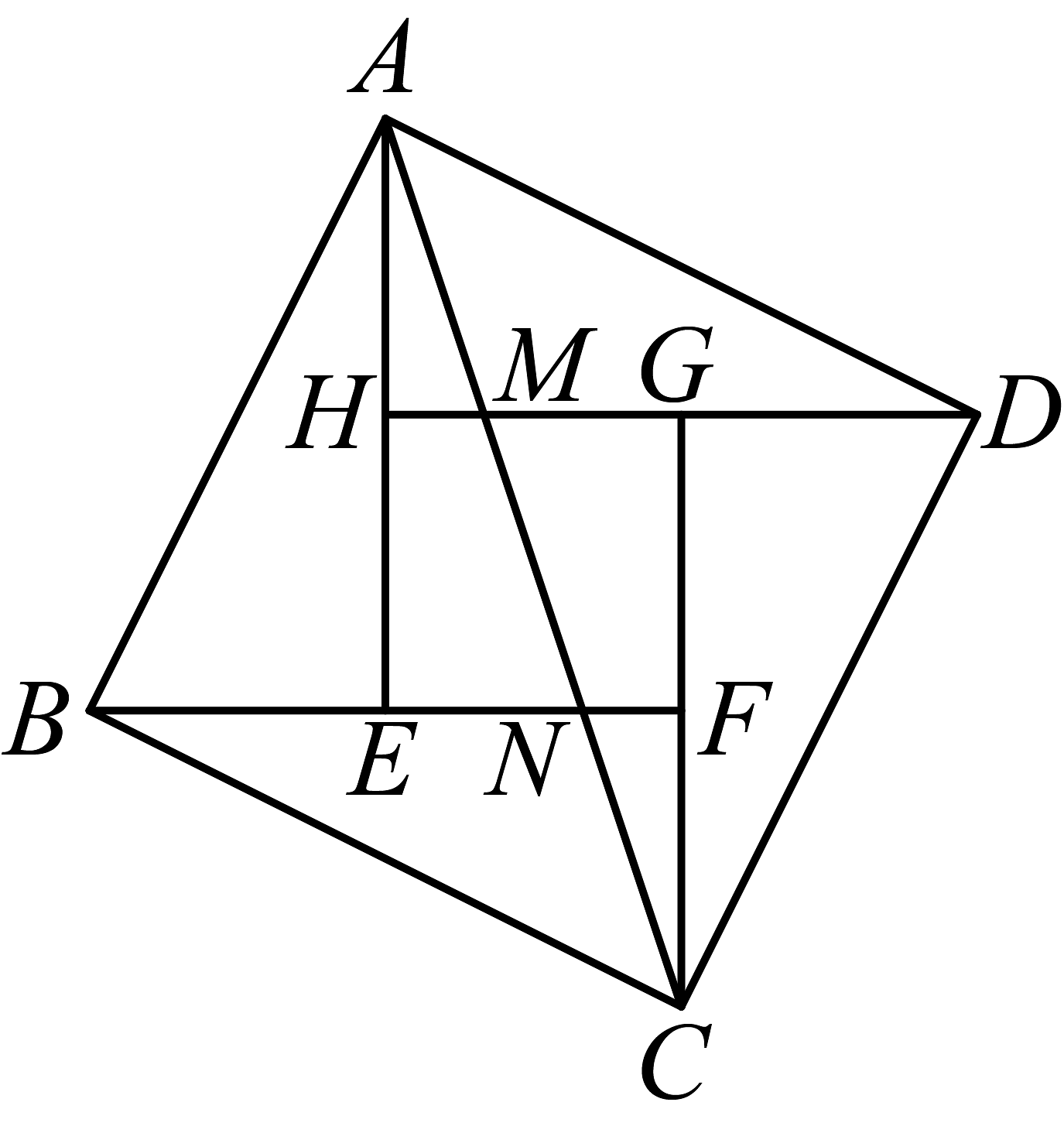
10、如图,正方形由四个全等的直角三角形( , , , )和中间一个小正方形组成,与 , 分别交于 , 两点,若 . 则长为 .
-
11、如图,为的直角边上一点,以为半径的半圆与斜边相切于点 , 交于点 . 已知 , , 则的长为 . (结果保留)

-
12、如图,在中, , , , , 记 , , 当不变,改变的过程中,下列代数式的值不变的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、反比例函数的图象上有 , 两点.下列正确的选项是( )A、当时, B、当时, C、当时, D、当时,
-
14、如图,四边形和四边形是位似图形,位似比为 , 且四边形的周长为36,则四边形的周长为( )
 A、16 B、24 C、54 D、81
A、16 B、24 C、54 D、81 -
15、2025年1月,中国人工智能企业深度求索宣布,其研发的智能助手的用户数量突破120000000,成为全球用户量最大的智能助手之一、数120000000用科学记数法表示为( )A、 B、 C、 D、
-
16、定义:对于一组关于x的多项式 , , , , 当其中两个多项式的乘积与另外两个多项式乘积的差为常数p时(不含字母x),称这样的四个多项式是一组黄金多项式,常数p的绝对值是这组黄金多项式的黄金因子.若多项式 , , , 是一组黄金多项式,黄金因子为2,则n的值为 .
-
17、综合实践
背景
随着我国科技事业的不断发展,国产无人机越来越多应用于实际生活,为人们的生活带来了便利.
素材1

某农业公司预购进A,B两种型号的植保无人机用来喷洒农药,A型机比B型机平均每小时少喷洒2公顷农田,A型机喷洒40公顷农田所用时间与B型机喷洒50公顷农田所用时间相等.
素材2
若农业公司共购进20架无人机,A型无人机5万元/架,B型无人机6万元/架.
问题解决
任务1
A,B两种型号无人机平均每小时分别喷洒多少公顷地?
任务2
若公司要求这批无人机每小时至少喷洒180公顷农田,那么该公司如何购买A型和B型无人机,才能使总成本最低?并求出最低成本.
-
18、 如图,长方形 AOBC,以 O 为坐标原点,OB、OA 分别在 x 轴、y 轴上,点 A 的坐标为 (0,8),点 B 的坐标为 (10,0),点 E 是 BC 边上一点,把长方形 AOBC 沿 AE 翻折后,C 点恰好落在 x 轴上点 F 处.
 (1)、 写出点 E、F 的坐标:E 的坐标 , F 的坐标.(2)、 求 AF 所在直线的函数关系式:(3)、 在 x 轴上求一点 P,使 成为等腰三角形,请直接写出所有符合条件的点 P 的坐标.
(1)、 写出点 E、F 的坐标:E 的坐标 , F 的坐标.(2)、 求 AF 所在直线的函数关系式:(3)、 在 x 轴上求一点 P,使 成为等腰三角形,请直接写出所有符合条件的点 P 的坐标. -
19、 如图所示为1个碗和4个整齐叠放成一摞的碗的示意图,碗的规格都一样. 小明尝试结合学习函数的经验,探究整齐叠放成一摞的这种规格的碗的总高度y(单位:cm)随着碗的数量x(单位:个)的变化规律. 下表是小明经过测量得到的y与x之间的对应数据:
x/个
1
2
3
4
y/cm
6
8.4
10.8
13.2
 (1)、 依据小明测量的数据,写出y与x之间的函数解析式,并说明理由.(2)、 若整齐叠放成一摞的这种规格的碗的总高度不超过31.2cm,则此时碗的数量最大为多少个?
(1)、 依据小明测量的数据,写出y与x之间的函数解析式,并说明理由.(2)、 若整齐叠放成一摞的这种规格的碗的总高度不超过31.2cm,则此时碗的数量最大为多少个? -
20、 如图,每个小正方形的边长都为1.
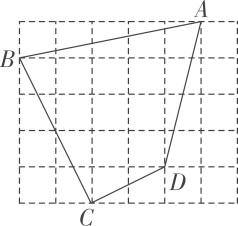 (1)、 利用勾股定理求出线段长: , , , ;(2)、 求证:.
(1)、 利用勾股定理求出线段长: , , , ;(2)、 求证:.