相关试卷

1、在“探索函数 $y = a x^{2} + b x + c$ 的系数a，b，c与图象的关系”活动中，老师给出了平面直角坐标系中的四个点：A（0，2），B（1，0），C（3，1），D（2，3）.同学们探索了经过这四个点中的三个点的二次函数的图象，发现这些图象对应的函数表达式各不相同，其中a 的最大值为（）

A、 $\frac{5}{2}$ B、 $\frac{3}{2}$ C、 $\frac{5}{6}$ D、 $\frac{1}{2}$

查看解析
2、一个二次函数图象，三名学生分别说出了它的一些特点.
甲：对称轴是直线x=4；
乙：与x轴两交点的横坐标都是整数；
丙：与y轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形面积为3；请写出满足上述全部特点的二次函数表达式：.

查看解析
3、已知两个相似三角形的相似比为3：4，且其中一个三角形的面积为16，则另一个三角形的面积为（）

A、12 B、9 C、12或 $\frac{16}{3}$ D、9或 $\frac{256}{9}$

查看解析
4、如图所示，在四边形ABCD 中，∠BAD=∠ADC=90°，AB=AD=2 $\sqrt{2}$ ， CD $= \sqrt{2},$ 点P 在四边形 ABCD 的边上.若点 P 到 BD 的距离为 $\frac{3}{2}$ ，则点 P 的个数为（）

A、1 B、2 C、3 D、4

查看解析
5、如图所示，在四边形ABCD 中，对角线AC，BD 相交于点O，OA=OC，添加一个条件，可使△AOB≌△COD.

查看解析
6、已知点 P（m，2）位于第二象限，则m 的值可以是（）

A、0 B、1 C、- 3 D、4

查看解析
7、课题小组学习“如何设计遮阳棚”时，计划在移门上方安装一个可伸缩的遮阳棚（如图甲)，其中AC 为移门的高度，B为遮阳棚固定点，BD 为遮阳棚的宽度（可变动)， $A B = 50 c m, A C = 210 c m, ∠ C B D = 8 0^{\circ} .$
小丁所在小组负责探究“移门在正午完全透光时太阳高度角与遮阳棚宽度的关系”，查阅得到如下信息：太阳高度角是指太阳光线与地平面的夹角；该地区冬至日正午的太阳高度角α最小（约 $3 5^{\circ});$ ；夏至日正午的太阳高度角α最大（约 $8 0^{\circ}) .$ .请你协助该小组，完成以下任务：

(1)、【任务1】如图乙，在冬至日正午时要使太阳光完全透过移门，BD 应该不超过多少长度?（结果精确到0.1cm)

(2)、【任务 2】如图丙，有一小桌子在移门的正前方，桌子最外端 E 到移门的距离为180cm，桌子高度MN=80cm.若要求在夏至日正午时太阳光恰好照射不到桌面，则BD 应该多长?（结果精确到0.1cm.参考数据： $s i n 5 5^{\circ} \approx$ 0. $82, c o s 5 5^{\circ} \approx 0.57, t a n 5 5^{\circ} \approx 1.43, s i n 10 \approx 0.17, c o s 1 0^{\circ} \approx 0.98, t a n 1 0^{\circ}$ ≈ $0.18, \sqrt{2} \approx 1.41)$

查看解析
8、某款折叠型的电脑支架由底座AB、电脑承载面CD 和长短两根转轴EB，EF 组成，在B，E，F 处安装有轴承，转轴BE，EF 可以自由转动， $A B =$ BE=2EF=20cm.某次展开后其侧面如图所示，此时 $A B ‖ C D, ∠ A B E =$ 54°，∠BEF=120°；
（参考数据： $s i n 5 4^{\circ} \approx 0.8090, c o s 5 4^{\circ} \approx 0.5878, t a n 5 4^{\circ} \approx$ 1.3764，sin24°≈0.4067，cos24°≈0.9135，tan24°≈0.4452)

(1)、求∠CFE 的度数.

(2)、求电脑承载面CD 与底座AB 之间的距离.（结果精确到0.1cm).

(3)、求轴承B，F之间的距离.

查看解析
9、如图所示，已知AB 是⊙O 的直径，BC 与⊙O 相切于点B，连结AC，OC.若 $s i n ∠ B A C = \frac{1}{3},$ 则 tan∠BOC=.

查看解析
10、在平面直角坐标系中，A（2，0)，B（4，4)，连结OB，AB，则 $t a n B;$ =若点C 在y轴上，作点C 关于直线OB，AB 的对称点D，E，则DE 的最小值为.

查看解析
11、如图所示，在△ABC 中，CD 是边AB 上的中线，∠B 是锐角， $s i n B = \frac{\sqrt{2}}{2},$ $t a n A = \frac{1}{2}, A C = \sqrt{5} .$

(1)、求∠B 的度数和AB 的长.

(2)、求 tan∠CDB 的值.

查看解析
12、《九章算术》是我国古代数学成就的杰出代表，其中“方田”章给出计算弧田面积所用公式如下：弧田面积 $= \frac{1}{2}$ （弦×矢+矢²)，弧田（如图所示)是由圆弧和其所对的弦所围成，公式中“弦”指圆弧所对弦长AB，“矢”等于半径长与圆心O到弦的距离之差.在如图所示的弧田中，“弦”为8，“矢”为3，那么cos∠OAB 的值为.

查看解析
13、如图甲所示为一台手机支架，图乙是其侧面示意图，AB，BC 可分别绕点A，B 转动，已知 BC=8cm，AB=16cm.当AB，BC 转动到∠BAE=60°，∠ABC=50°时，点C 到AE 的距离为 cm.（结果保留一位小数，参考数据： $s i n 7 0^{\circ} \approx 0.94, \sqrt{3} \approx 1.73)$

查看解析
14、第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图所示，在由四个全等的直角三角形（△DAE，△ABF，△BCG，△CDH)和中间一个小正方形EFGH 拼成的大正方形ABCD 中，∠ABF>∠BAF，连结BE.设∠BAF=α，∠BEF=β，若正方形EFGH 与正方形ABCD 的面积之比为1： n，tanα=tan²β，则n=.

查看解析
15、如图所示，在正方形网格中，每个小正方形的边长都是1，⊙O 是△ABC 的外接圆，点A，B，O在网格线的交点上，则sin∠ACB 的值是.

查看解析
16、如图所示，有一天桥高AB 为5米，BC 是通向天桥的斜坡，∠ACB=45°，市政部门启动“陡改缓”工程，决定将斜坡的底端C延伸到D 处，使∠D=30°，则CD 的长度约为（参考数据： $\sqrt{2} \approx 1.414, \sqrt{3} \approx 1.732 ）$ （ )

A、1.59米 B、2.07米 C、3.55米 D、3.66米

查看解析
17、在△ABC 中， $A B = A C, s i n B = \frac{3}{5},$ 且△ABC 的周长为36，则此三角形的面积为（ )

A、12 B、24 C、48 D、96

查看解析
18、如图所示，在正方形网格中，∠1，∠2，∠3的大小关系为（ )

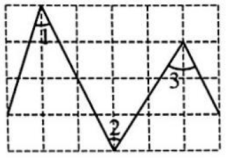A、∠1=∠2=∠3 B、∠1<∠2<∠3 C、∠1=∠2>∠3 D、∠1<∠2=∠3

查看解析
19、在△ABC中，∠C=90°，设∠A，∠B，∠C 所对的边分别为a，b，c，则（ )

A、c=b·sin B、B. b=c·sinB C、a=b ·tanB D、b=c·tanB

查看解析
20、数学中的很多恒等式可以通过计算面积得到.如图甲所示，可以求出阴影部分的面积是 $a^{2} - b^{2};$ 把图甲中的阴影部分裁剪下来，重新拼成一个长方形，如图乙所示，它的长是（ $a + b,$ 宽是 $a - b .$ .比较图甲、图乙中阴影部分的面积，可以得到恒等式 $(a + b) (a - b) = a^{2} - b^{2} .$

(1)、观察图丙，请你写出（ ${(a + b)}^{2}, {(a - b)}^{2},$ ab之间的一个恒等式： ${(a + b)}^{2}$ $=$ .

(2)、根据（1）中的结论，若 ${(x + y)}^{2} = 10, {(x - y)}^{2} = 2,$ 求下列各式的值：
①xy；
② $x^{2} + y^{2} .$

查看解析

上一页 605 606 607 608 609 下一页跳转