-
1、一个仅装有球的不透明布袋里有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为 ， 则n=.
-
2、某地林业局考察一种树苗移植的成活率，将调查数据绘制成统计图如图34-4，则可估计这种树苗移植成活的概率约是( )
A、0.95 B、0.90 C、0.85 D、0.80 -
3、有7 张扑克牌如图所示，将其打乱顺序后，背面朝上放在桌面上.若从中随机抽取一张，则抽到的花色可能性最大的是图中的( )
A、
B、
C、
D、
-
4、某校计划组织研学活动，现有四个地点可供选择：南鹿岛、百丈漈、楠溪江、雁荡山.若从中随机选择一个地点，则选中“南麂岛”或“百丈漈”的概率为( )A、 B、 C、 D、
-
5、下列说法正确的是( )A、10张票中有1张奖票，10人去摸，先摸的人摸到奖票的概率较大 B、从1，2，3，4，5 中随机抽取一个数，取得偶数的可能性较大 C、小强一次掷出3 枚质地均匀的骰子，3枚全是6点朝上是随机事件 D、抛一枚质地均匀的硬币，正面朝上的概率为 ， 连续抛此硬币2次必有1次正面朝上
-
6、综合实践：如何测量出路灯的灯杆和灯管支架的长度?
素材1：如图①，一种路灯由灯杆AB和灯管支架 BC两部分构成，已知灯杆AB与地面垂直，灯管支架 BC 与灯杆AB 的夹角∠ABC=127°.
素材2：如图②，在路灯正前方的点 D 处测得∠ADB=37°，∠ADC=45°，AD=400 cm.
根据以上素材解决问题：
(结果精确到 1 cm.参考数据： sin 37°≈0.60， cos 37°≈0.80， tan 37°≈0.75)
(1)、求灯杆 AB 的长度；(2)、求灯管支架 BC的长度. -
7、如图①是一个放置在水平地面上的长方体密封容器，内部装有水，其正方形底面的边CD=8cm，棱AD上标有刻度，水面与AD 交于点M，读得DM=30 cm，如图②将容器放在斜坡 OE上，此时水面分别与 AD，BC交于点 N，P(NP∥OF)，读得 DN=25 cm.若容器厚度不计，则tan∠ANP=.
-
8、教室里的投影仪投影时，可以把投影光线CA，CB及在黑板上的投影图像高度AB 抽象成如图所示的△ABC，∠BAC=90°，黑板上投影图像的高度AB=120 cm，CB 与 AB 的夹角∠B=33.7°，求 AC的长(结果精确到 1 cm.参考数据： sin 33.7°≈0.55，cos33.7°≈0.83， tan 33.7°≈0.67).
-
9、如图，在△ABC 中，AB= 则 cos C的值为.
-
10、 如图所示的四边形 OABC，若AB=BC=1，∠AOB=30°，OA⊥AB，OB⊥BC，则点 B 到 OC 的距离为( )
A、 B、 C、1 D、2 -
11、某路灯的示意图如图，已知它是轴对称图形，若∠ACB=140°，AC=BC=1.6m，CD垂直于地面且CD=8 m，则点 A 到地面的高度为( )
A、(8+1.6sin 20°)m B、(8+1.6cos 20°)m C、 D、 -
12、第 14 届国际数学教育大会(ICME-14)会标如图①所示，会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图②所示的“弦图”是由四个全等的直角三角形(△ABE，△BCF，△CDG，△DAH)和一个小正方形 EFGH拼成的大正方形ABCD.若EF：AH=1：3，则sin∠ABE=( )
A、 B、 C、 D、 -
13、 如图所示，有一天桥的高AB 为5米，BC是通向天桥的斜坡，∠ACB=45°，市政部门启动“陡改缓”工程，决定将斜坡的底端C延伸到 D 处，使∠D=30°，则 CD 的长约为(参考数据： ( )
A、1.59米 B、2.07米 C、3.55米 D、3.66米 -
14、如图所示，若格点三角形 ABC放置在5×4 的正方形网格中，则sin∠ABC的值为( )
A、 B、 C、 D、 -
15、cos 30°等于( )A、 B、 C、 D、
-
16、如图，△ABC内接于⊙O，直径 BD 交边 AC于点 E，过点C 作 CH⊥AB 于点 H，交 BD 于点 F，连结 CD.
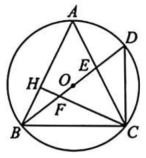(1)、求证：∠ACH=∠DBC.(2)、若AB=AC，①当△BCE是等腰三角形时，求∠BAC 的度数；
②若 求 DE： EF的值.
-
17、如图①，AB为⊙O的直径，CD⊥AB于点E， BF与CD交于点G.
(1)、求证：CD=BF；(2)、若BE=1，BF=4，求GE的长；(3)、连结GO，OF，如图②，求证：2∠EOG+ -
18、如图，四边形 ABCD 内接于 ⊙O，BC∥AD， AC ⊥ BD. 若 ， 则∠CAO的度数与 BC 的长分别为( )
A、10°，1 B、 C、15°，1 D、 -
19、 如图，OA，OB，OC 都是⊙O的半径，∠ACB=2∠BAC.
(1)、求证：∠AOB=2∠BOC；(2)、若AB=4，BC= ， 求⊙O的半径. -
20、 如图，AD 是⊙O的直径，△ABC是⊙O的内接三角形.若∠DAC=∠ABC，AC=4，则⊙O的直径AD=.
