-
1、判断方程|x-2|的根的情况是( )A、有四个实数根 B、有两个实数根 C、有一个实数根 D、无实数根
-
2、若关于x的一元二次方程x2+2mx+m2-m+1=0没有实数根,则实数m的取值范围是( )A、m<1 B、m>1 C、m>-1 D、m<-1
-
3、若关于x的一元二次方程x2-4x+m=0有两个相等的实数根,则实数m的值为( )A、4 B、-4 C、±4 D、2
-
4、已知关于x的一元二次方程x2+2x-1=0的两个实数根分别为x1和x2 , 则x1+x2+x1•x2的值为( )A、-3 B、-1 C、-2 D、0
-
5、一元二次方程x2-20x+100=0的根的情况是( )A、有两个不相等的实数根 B、没有实数根 C、有两个相等的实数根 D、只有一个实数根
-
6、如图,在平面直角坐标系中,点A,B的坐标分别为 , . 将线段向下平移2个单位长度,再向左平移5个单位长度,得到线段 , 连接;
 (1)、直接写出坐标:点C , 点D .(2)、M,N分别是线段上的动点,点M从点A出发向点B运动,速度为每秒1个单位长度,点N从点D出发向点C运动,速度为每秒0.5个单位长度,若两点同时出发,假设运动时间为t,请写出M,N的坐标(用含t的式子表示),并求几秒后轴?(3)、点P是直线上一个动点,连接 , 当点P在直线上运动时,请画出图形并写出与的数量关系.
(1)、直接写出坐标:点C , 点D .(2)、M,N分别是线段上的动点,点M从点A出发向点B运动,速度为每秒1个单位长度,点N从点D出发向点C运动,速度为每秒0.5个单位长度,若两点同时出发,假设运动时间为t,请写出M,N的坐标(用含t的式子表示),并求几秒后轴?(3)、点P是直线上一个动点,连接 , 当点P在直线上运动时,请画出图形并写出与的数量关系. -
7、在平面直角坐标系中,已知点 , , 且a和b满足 .
 (1)、请直接写出B点坐标:B;(2)、请在x轴上找点C,使得 , 求出点C的坐标;(3)、点 , , 连接 , 交于点M,在线段上存在点P,使 , 求出点P的坐标.
(1)、请直接写出B点坐标:B;(2)、请在x轴上找点C,使得 , 求出点C的坐标;(3)、点 , , 连接 , 交于点M,在线段上存在点P,使 , 求出点P的坐标. -
8、我们将四个全等的菱形按图(1)所示组合的图形称为一个基本图,将此基本图复制并向右平移,使得其中一个菱形重合,得到图(2),图(3),….
 (1)、观察上图并完成下表:
(1)、观察上图并完成下表:基本图的个数
1
2
3
4
. ..
菱形的个数
5
9
13
①
. ..
猜想:在图(n)中,菱形的个数为②个(用表示);
(2)、如图,将图(n)放在直角坐标系中,使得第一个基本图的对称轴为直线 , 第二个基本图的对称轴为直线 , 则其中第2025个基本图的对称轴是③ , 图(2025)的对称轴为④ .
-
9、在平面直角坐标系xOy中,点 , 若 , 则称点与点互为“神秘点”.例如,点 , 点 , 因为 , 所以点与点互为“神秘点”.(1)、若点的坐标是 , 且点与点互为“神秘点”,求的值.(2)、若点与“神秘点”互为“神秘点”,若m,n均为正整数,求点的坐标.
-
10、如图,已知的三个顶点坐标分别是 .
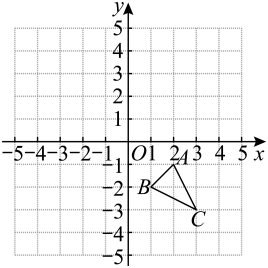 (1)、将向上平移个单位长度得到 , 请画出;(2)、请直接写出的坐标;(3)、求的面积.
(1)、将向上平移个单位长度得到 , 请画出;(2)、请直接写出的坐标;(3)、求的面积. -
11、如图,在直角坐标系中,的位置如图所示,请回答下列问题:
 (1)、画出关于轴的对称图形;(2)、的面积为 .
(1)、画出关于轴的对称图形;(2)、的面积为 . -
12、已知点 , 解答下列各题.(1)、若点P在y轴上,则;(2)、点Q的坐标为 , 直线轴,求点P的坐标;
-
13、如图,这是厦门市部分简图,请以火车站为坐标原点建立平面直角坐标系,并分别写出各地的坐标(火车站除外).

-
14、如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“”方向排列,如 , , , , , , ……,根据这个规律探索可得,第2025个点的坐标为 .

-
15、如图,在平面直角坐标系中,已知的顶点坐标分别为 , , . 若在第二象限内有一点 , 且四边形的面积是的面积的 , 则点P的坐标为 .

-
16、已知线段 , 轴,若点M坐标为 , 点N在第二象限,则N点的坐标为 .
-
17、在平面直角坐标系中,已知点 , 长度为3的线段与x轴平行,则点Q的坐标是 .
-
18、将点向右平移1个单位长度,再向下平移3个单位长度后,得到点 , 则点的坐标为 .
-
19、在平面直角坐标系中,已知点在轴上,则的值是 .
-
20、点到y轴的距离为 .