-
1、如图所示的是甲、乙两个家庭某季度支出情况统计图.关于教育经费的支出,下列结论正确的是( )
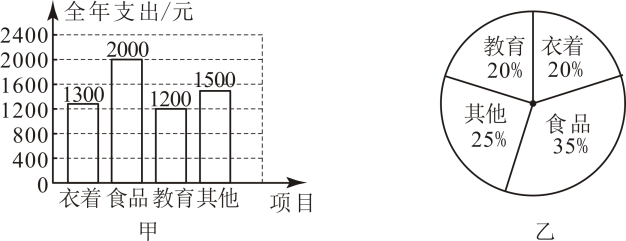 A、甲比乙多 B、乙比甲多 C、甲和乙一样多 D、无法比较
A、甲比乙多 B、乙比甲多 C、甲和乙一样多 D、无法比较 -
2、学校团委以“我最喜欢的书籍”为主题,对全校学生进行抽样调查,收集整理喜爱的书籍类型(只选一种,A.科普,B.文学,C.体育,D.其他)数据后,绘制出两幅尚未完成的统计图,如图所示.则下列说法错误的是( )
 A、此次调查共抽查了400名学生 B、类型D所对应的扇形的圆心角为36° C、类型B的人数为120人 D、类型C所占百分比为30%
A、此次调查共抽查了400名学生 B、类型D所对应的扇形的圆心角为36° C、类型B的人数为120人 D、类型C所占百分比为30% -
3、某次考试中,班级的数学成绩统计图如图所示(每组包含最小值,不包含最大值),下列说法错误的是( )
 A、组距为10 B、该班的总人数为40 C、最低分为50分 D、及格(≥60分)率为90%
A、组距为10 B、该班的总人数为40 C、最低分为50分 D、及格(≥60分)率为90% -
4、根据某地居民家庭亲子阅读消费调查报告中的相关数据制成扇形统计图如图所示,由图可知,下列说法错误的是( )
 A、扇形统计图能反映各部分在总体中所占的百分比 B、每天阅读30 min以上的居民家庭超过50% C、每天阅读1 h以上的居民家庭占20% D、每天阅读30 min以上至1 h的居民家庭对应扇形的圆心角是108°
A、扇形统计图能反映各部分在总体中所占的百分比 B、每天阅读30 min以上的居民家庭超过50% C、每天阅读1 h以上的居民家庭占20% D、每天阅读30 min以上至1 h的居民家庭对应扇形的圆心角是108° -
5、某汽车公司销售A,B,C,D,E五种品牌新能源汽车,其续航里程(单位:km)如表所示,根据表中的数据制作统计图,为了更清楚地表示出每种新能源汽车的续航里程,应选择( )
品牌
A
B
C
D
E
续航里程/km
650
500
350
750
450
A、条形统计图 B、折线统计图 C、扇形统计图 D、以上都不对 -
6、下列数据为定性数据的是( )A、某同学的立定跳远成绩 B、春节档某部电影大年初一当天的票房 C、某校所有教师的学历情况 D、全班同学家养的宠物的数量
-
7、下列调查适宜采用普查方式的是( )A、了解山西省七年级学生的健康状况 B、了解一批灯泡的使用寿命 C、神舟十四号发射前,对各个零部件进行检查 D、了解某品牌的新能源电动汽车的蓄电池的性能
-
8、某区教师进修学院为了督查国家双减政策的落实情况,现调查某校学生每日睡眠时长,选用下列哪种方法最恰当( )A、查阅文献资料 B、对学生进行问卷调查 C、上网查询 D、对校领导进行问卷调查
-
9、为了增强学生的环保意识,某校组织了一次全校2 000名学生都参加的“环保知识”测试,测试题共10道题.测试结束后,学校团委随机抽查部分学生的测试卷,对学生答题情况进行分析统计,发现所抽查的测试卷中答对题量最少为6道,并且绘制了如下两幅不完整的统计图.请根据统计图提供的信息解答以下问题.
 (1)、本次抽查的样本容量是;在扇形统计图中,m= , n=C所对应扇形的圆心角为度.(2)、将条形统计图补充完整.(3)、请根据以上调查结果,估计该校答对不少于8道题的学生有多少名.
(1)、本次抽查的样本容量是;在扇形统计图中,m= , n=C所对应扇形的圆心角为度.(2)、将条形统计图补充完整.(3)、请根据以上调查结果,估计该校答对不少于8道题的学生有多少名. -
10、为了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制了如下两个尚不完整的统计图表.
组别
零花钱的数额x/元
人数
0≤x<30
4
30≤x<60
16
60≤x<90
a
90≤x<120
b
x≥120
2

请根据以上图表,解答下列问题.
(1)、这次被调查的同学共有人, , m=.(2)、求扇形统计图中扇形C的圆心角的度数.(3)、若该校共有学生1000人,请估计每月零花钱的数额在的人数. -
11、小明为了了解本校学生的假期活动方式,随机对本校的部分学生进行了调查.收集整理数据后,小明将假期活动方式分为五类:A.读书看报;B.健身活动;C.做家务;D.外出游玩;E.其他方式,并绘制了不完整的统计图如图.统计后发现“做家务”的学生人数占调查总人数的20%.请根据图中的信息解答下列问题.
 (1)、本次调查的总人数是.(2)、补全条形统计图.(3)、根据调查结果,估计本校2360名学生中假期活动方式是“读书看报”的有多少名.
(1)、本次调查的总人数是.(2)、补全条形统计图.(3)、根据调查结果,估计本校2360名学生中假期活动方式是“读书看报”的有多少名. -
12、某学校有1500名学生参加首届以“我爱我们的课堂”为主题的图片制作比赛,赛后随机抽取其中的100名参赛学生的成绩进行整理并制作成图表如下.

分数段x/分 人数(频数) 60≤x<70 40 70≤x<80 35 80≤x<90 a 90≤x≤100 10
请根据上述信息,解答下列问题.(1)、表中 .(2)、请补全频数直方图.(3)、如果将比赛成绩80分以上(含80分)定为优秀,那么优秀率是多少? 估计该校参赛学生获得优秀的有多少名. -
13、某企业开展“一周工作量完成情况”的调查活动,随机调查了部分员工一周的工作量剩余情况,并将调查结果统计后绘制成如图①和图②所示的不完整的统计图.
 (1)、被调查的员工人数为.(2)、把条形统计图补充完整.(3)、若该企业有员工10 000人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人.
(1)、被调查的员工人数为.(2)、把条形统计图补充完整.(3)、若该企业有员工10 000人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人. -
14、对八年级50名学生进行调查,得到下表.
喜欢的科目
数学
物理
英语
语文
人数/名
40
20
30
25
根据上表回答下列问题.
(1)、计算喜欢各个科目的人数占全体被调查人数的百分比.(2)、上述百分比能否用扇形统计图表示? 为什么? -
15、某校六(2)班的学生在植树节开展“植树造林,绿化城市”的活动,本次活动结束后,该班植树情况的部分统计图如图所示,那么该班的总人数是.

-
16、每年5月11日是由世界卫生组织确定的“世界防治肥胖日”,某校为了解全校2 000名学生的体重情况,随机抽测了200名学生的体重,根据体质指数标准,体重超标的有15名学生,则估计全校体重超标的学生有名.
-
17、为了了解某区初中学生的视力情况,随机抽取了该区500名初中学生进行调查.整理样本数据,得到下表.
视力
4.7以下
4.7
4.8
4.9
4.9以上
人数/名
102
98
80
93
127
根据抽样调查结果,估计该区12 000名初中学生视力不低于4.8的有名.
-
18、某实验中学六(1)班全体同学的综合素质评价“运动与健康”方面的等级统计如图所示,其中评价为“A”所在扇形的圆心角是度.

-
19、为了解某市老人的身体健康状况,在以下抽样调查中,你认为样本选择较好的是.(填序号)
①100位女性老人;②公园内100位老人;③在城市和乡镇选10个点,每个点任选10位老人.
-
20、调查我市一批药品的质量是否符合国家标准,采用的方式更合适.(填“全面调查”或“抽样调查”)