-
1、 若把能表示为两个连续偶数的平方差的正整数叫做神秘数.请你根据“神秘数”的定义判断8,12,20,28,2004是神秘数吗? 为什么?
-
2、 把下列命题改写成“如果……那么……”的形式.(1)、一个锐角的补角是钝角;(2)、到一条直线距离相等的两条直线互相平行.
-
3、 将命题“末位数是0或5的整数能被5整除”改写成“如果……那么……”的形式.
-
4、 将命题“负数的绝对值是它的相反数”改写成“如果……那么……”的形式.
-
5、 将命题“互为相反数的两数之和为0”改写成“如果……那么……”的形式.
-
6、 指出下列命题的条件和结论,并改写成“如果……那么……”的形式.(1)、两直线平行,内错角相等;(2)、三角形内角和等于180°.
-
7、 下列语句是命题的有.(填序号)
①1是正整数;
② 是无理数;
③明天会下雨吗?
④三角形的两边之和大于第三边吗?
-
8、 语句“两个有理数的和仍是有理数”定义.(填“属于”或“不属于”)
-
9、 将命题“同角的补角相等”改写成“如果……那么……”的形式,正确的是( )A、如果两个角相等,那么这两个角的补角相等 B、如果两个角的补角相等,那么这两个角相等 C、如果两个角相等,那么这两个角是同一个角的补角 D、如果两个角是同一个角的补角,那么这两个角相等
-
10、 将命题“同位角相等”改写成“如果……那么……”的形式,正确的是( )A、如果两直线平行,那么同位角相等 B、如果两个角相等,那么它们是同位角 C、如果同位角相等,那么两直线平行 D、如果两个角是同位角,那么这两个角相等
-
11、 下列选项中的语句属于命题的是( )A、若|a|=a,则a≥0 B、画∠AOB的平分线 C、延长AB至点C D、作一条直线和已知直线垂直
-
12、 下列语句是不是命题? 如果是命题,请写出它的条件与结论.(1)、若|a|=|b|,则(2)、若 ab>0,则a>0,b>0.
-
13、 把命题“全等三角形的对应角相等”改写成“如果……那么……”的形式为.
-
14、 命题“如果a⊥c,b⊥c,那么a∥b”的条件是( )A、a⊥c B、b⊥c C、a⊥c,b⊥c D、a∥b
-
15、 关于命题“内错角相等,两直线平行”的条件和结论,下列选项中的说法正确的是 ( )A、条件是内错角相等,结论是两直线平行 B、条件是两直线平行,结论是内错角相等 C、条件和结论都是内错角相等 D、条件和结论都是两直线平行
-
16、 下列选项中的语句属于定义的是( )A、若a>b,则a-b>0 B、两直线平行,同位角相等 C、对顶角相等 D、有一个角是直角的三角形叫做直角三角形
-
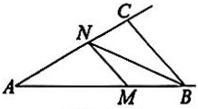
17、如图,在 中, , M是射线AB上的一个动点,过点M作 交AC于点N.当 是等腰三角形时,求的度数.
-
18、如图,在 中, 点D在边AB上,
 (1)、求 的度数;(2)、过点A作 交CD的延长线于点E.求证:是等腰三角形.
(1)、求 的度数;(2)、过点A作 交CD的延长线于点E.求证:是等腰三角形. -
19、如图,在 中, , CD是AB边上的中线,将 沿直线AC折叠,使点D落在点E处,得到四边形ABCE.求证:.

-
20、 如图,在 的方格纸中,线段AB的两个端点A,B都在小方格的格点上.按要求画一个三角形,使它的顶点在小方格的格点上.
 (1)、以线段AB为一腰画一个锐角等腰 , 在图1中画出示意图;(2)、以线段AB为一腰画一个直角等腰 , 在图2中画出示意图.
(1)、以线段AB为一腰画一个锐角等腰 , 在图1中画出示意图;(2)、以线段AB为一腰画一个直角等腰 , 在图2中画出示意图.