-
1、 如图,四边形是菱形,于点E , 则的长是( )
 A、 B、6 C、 D、12
A、 B、6 C、 D、12 -
2、 用配方法解方在 , 下列配方正确的是( )A、 B、 C、 D、
-
3、 若分式的值为零,则等于( )A、 B、0 C、2 D、0和
-
4、 如图,为了测量湖两岸、两点间的距离,可在、外选一点 , 再确定、的中点、 , 测得 , 则两点间的距离是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、 教育部门高度重视校园安全教育,要求各级各类学校从认识安全警告标志入手开展安全教育,下列安全图标既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
6、综合与实践
问题情境:某小区的社区管理人员计划在临街的拐角建造一块绿化地(阴影部分),现面向小区居民征集设计方案,欣欣和强强合作一起完成了绿化地和引水灌溉方案的设计.
欣欣设计的绿化地及浇灌点方案如下:如图, , 在上选取两点E , F为浇灌点,从水源点G处铺设管道引水.
强强设计的铺设管道方案如下:
方案一:从水源点G处直接铺设管道分别到浇灌点E , F;
方案二:过点G作的垂线,垂足为H , 先从水源点G处铺设管道到点H处,再从点H处分别向浇灌点E , F铺设管道.
社区管理人员按照欣欣设计的绿化地及浇灌点方案施工,施工人员在只有卷尺的情况下,通过测量某两点之间的距离,就确定了 .
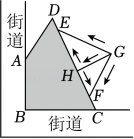 (1)、施工人员测量的是点与点之间的距离.(2)、若绿化地建造每平方米的费用为100元,求建造绿化地的费用.(3)、若 , , 管道铺设费用为50元/米,请比较强强设计的两种铺设管道方案所花的费用,并求出铺设管道所需的最少费用.
(1)、施工人员测量的是点与点之间的距离.(2)、若绿化地建造每平方米的费用为100元,求建造绿化地的费用.(3)、若 , , 管道铺设费用为50元/米,请比较强强设计的两种铺设管道方案所花的费用,并求出铺设管道所需的最少费用. -
7、如图1,∠DAB=90°,CD⊥AD于点D , 点E是线段AD上的一点,若DE=AB , DC=AE .
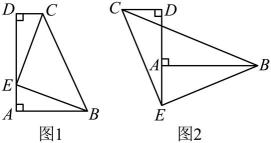 (1)、判断CE与BE的关系是 .(2)、如图2,若点E在线段DA的延长线上,过点D在AD的另一侧作CD⊥AD , 并保持CD=AE , DE=AB , 连接CB , CE , BE , 试说明(1)中结论是否成立,并说明理由.
(1)、判断CE与BE的关系是 .(2)、如图2,若点E在线段DA的延长线上,过点D在AD的另一侧作CD⊥AD , 并保持CD=AE , DE=AB , 连接CB , CE , BE , 试说明(1)中结论是否成立,并说明理由. -
8、某超市最近销售蓝莓,根据以往的销售经验,每天的售价与销售量之间有如下关系:
每千克售价(元)
60
59
58
57
56
……
30
每天销售量(千克)
50
55
60
65
70
……
200
(1)、表格中的自变量是 , 因变量是 .(2)、设当售价从每千克60元下降了x元时,每天销售量为y千克,直接写出y与x之间的关系式;(3)、如果周六的销售量是170千克,那这天的售价是每千克多少元?(4)、如果蓝莓的成本价是30元/千克,某天的售价定为40元/千克,当天的销售利润是多少? -
9、如图,在中, , , , 点D是外一点,连接 , , 且 , .
 (1)、求证:;(2)、求四边形面积.
(1)、求证:;(2)、求四边形面积. -
10、(1)、计算: .(2)、求式中的值:
-
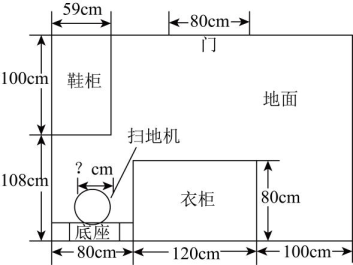
11、为了体验人工智能生活,小洪想购入一款圆形扫地机放置在如图所示的衣帽间的角落(鞋柜、衣柜与地面均无缝隙),在没有障碍物阻挡的前提下,扫地机能从底座脱离后打扫全屋地面.已知该圆形扫地机有如下5款尺寸(直径): , , , , , 则其中有款扫地机可以购买.
-
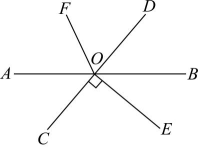
12、如图,直线与相交于点 , 于点平分 , 且 , 则的度数为°.
-
13、农民麦子大丰收,小彬用打印机制作了一个底面周长为 , 高为的圆柱粮仓模型(如图所示).现要在此模型的侧面贴彩色装饰带,使装饰带从柱底沿圆柱表面均匀地缠绕2圈到达柱顶正上方(从点到点为的中点),则装饰带的长度最短为( )
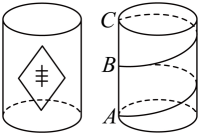 A、 B、 C、 D、
A、 B、 C、 D、 -
14、以下四种情景分别描述了两个变量之间的关系:
①将水箱中的水匀速放出,直至放完,水箱中的剩余水量与放水时间的关系.②在受力范围内,弹簧的长度与弹簧受到的拉力的关系.③汽车以某一固定的速度匀速行驶,行驶的路程与时间的关系.④周末,小亮从家到体育馆,打了一段时间的篮球后,按原速度原路返回,小亮离家的距离与时间的关系.
下面四个图象分别刻画了以上变量之间的关系,图象对应的情景的正确排序是( )
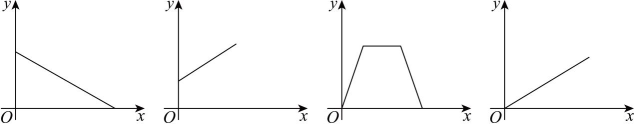 A、①②③④ B、①④③② C、①②④③ D、②④③①
A、①②③④ B、①④③② C、①②④③ D、②④③① -
15、如图,点E在的延长线上,对于给出的四个条件:
①;②;③;④ .
其中能判断的是( )
 A、①② B、①④ C、①③ D、②④
A、①② B、①④ C、①③ D、②④ -
16、用如下方式确定甲、乙两支足球队比赛谁先开球,公平的方式有( )种.
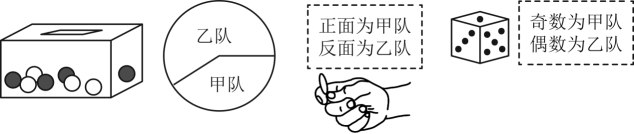 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
17、已知 , , 则( )A、14.36 B、143.6 C、45.4 D、454
-
18、如图,在三角形中, , , , 垂足为点D , 则的长可能是( )
 A、4 B、6 C、8 D、10
A、4 B、6 C、8 D、10 -
19、在实数 , 0, , , , , (相邻两个6之间1的个数逐次加1)中,无理数有( )A、2个 B、3个 C、4个 D、5个
-
20、下列计算中,结果正确的是( )A、 B、 C、 D、