-
1、点向左平移2个单位后的坐标是 .
-
2、如图,E是的中点,平分 . 有下列结论:其中正确的是( )
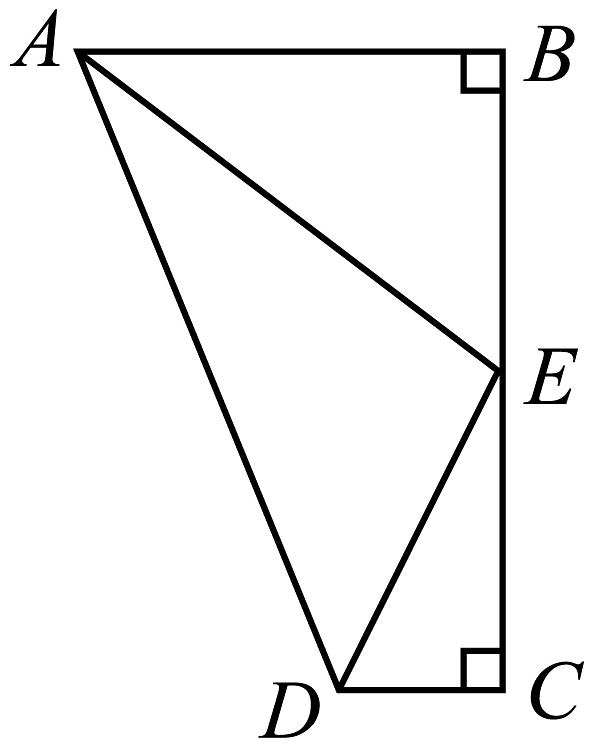 A、②③ B、①②④ C、②③④ D、①②③④
A、②③ B、①②④ C、②③④ D、①②③④ -
3、将点向右平移3个单位,再向上平移2个单位后的坐标是( )A、 B、 C、 D、
-
4、如图,在中,D是中点,E是中点,则的长等于的( )
 A、两倍 B、一倍 C、一半 D、无法确定
A、两倍 B、一倍 C、一半 D、无法确定 -
5、正方形具有而矩形不一定具有的性质是( )A、对角线相等 B、对角线互相平分 C、四个角都是直角 D、对角线互相垂直
-
6、若点在第二象限,则点在第( )象限A、一 B、二 C、三 D、四
-
7、菱形的两条对角线长分别为6和8,则它的面积是( )A、24 B、48 C、12 D、18
-
8、下列条件中,能判定四边形是平行四边形的是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、邻边相等
-
9、正六边形的每个内角为( )A、60° B、120° C、150° D、170°
-
10、 如图,在矩形中, , . 点从点出发向点运动,运动到点即停止;同时,点从点出发向点运动,运动到点即停止,点、的速度都是 . 连接、、 , 设点、运动的时间为 .
 (1)、求当为何值时,四边形
(1)、求当为何值时,四边形 矩形; (2)、求当为何值时,四边形是菱形;(3)、在运动过程中,沿着把翻折,求当为何值时,翻折后点的对应点恰好落在边上.
矩形; (2)、求当为何值时,四边形是菱形;(3)、在运动过程中,沿着把翻折,求当为何值时,翻折后点的对应点恰好落在边上. -
11、 某商店以元千克的单价进货了一批商品,经调查发现,每天的销售量千克与销售单价元千克之间的函数关系如图中线段所示.
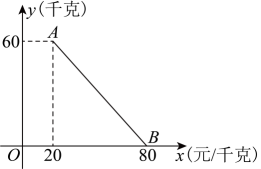 (1)、求与的函数表达式;(2)、要使每天的销售利润达到元,销售单价应定为每千克多少元?
(1)、求与的函数表达式;(2)、要使每天的销售利润达到元,销售单价应定为每千克多少元? -
12、 仁寿县鳌峰中学组织学生开展了“青春心向党,红色永传承”党史知识竞赛,为了解学生对党史的掌握情况,该校随机抽取了部分学生的竞赛成绩,将成绩分为A , B , C , D四个等级,并绘制成如图所示的两幅不完整的统计图
 (1)、本次共抽取了 ▲ 名学生的竞赛成绩,并补全条形统计图;(2)、若本校共有3200人参加本次竞赛活动,请估计竞赛成绩为B等级的学生人数;(3)、学校在竞赛成绩为A等级中的甲、乙、丙、丁这4名学生里,随机选取2人参加学校党史报告活动,用画树状图或列表法求出甲、乙两人同时被选中的概率.
(1)、本次共抽取了 ▲ 名学生的竞赛成绩,并补全条形统计图;(2)、若本校共有3200人参加本次竞赛活动,请估计竞赛成绩为B等级的学生人数;(3)、学校在竞赛成绩为A等级中的甲、乙、丙、丁这4名学生里,随机选取2人参加学校党史报告活动,用画树状图或列表法求出甲、乙两人同时被选中的概率. -
13、 已知关于x的方程 .(1)、若该方程的一个根为 , 求m的值;(2)、求证:不论m取何实数,该方程总有实数根.
-
14、 小颖和小红在化简的过程中,分别给出如下的部分运算过程.
小颖:原式
…
小红:原式
…
(1)、小颖解法的依据是 , 小红解法的依据是 .A.分式的基本性质 B.等式的基本性质 C.乘法结合律 D.乘法分配律
(2)、请你选择一种解法,写出完整的解答过程,并从“ , , ”中选一个合适的数作为的值,代入求该分式的值. -
15、 解方程(1)、;(2)、 .
-
16、(1)、解不等式组: , 并把不等式组的解集在数轴上表示出来;
 (2)、因式分解: .
(2)、因式分解: . -
17、 如图,中, , , . 点是边上的动点,过点作边 , 的垂线,垂足分别为 , . 连接 , 则的最小值为 .

-
18、 将点沿x轴方向向右平移3个单位,再沿y轴方向向上平移2个单位,所得的点的坐标是 .
-
19、 分解因式: .
-
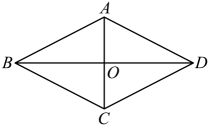
20、 如图,在菱形中,已知 , 则 .