-
1、如图所示为某摩天轮的示意图,其直径为90 m,旋转1周用时15 min.小明从摩天轮的底部(与地面相距0.5m)出发开始观光,摩天轮转动1周,小明在离地面68m及以上的空中停留的时间为( )
 A、3min B、5m in C、6m in D、10 min
A、3min B、5m in C、6m in D、10 min -
2、如图,某水渠的横断面是梯形,其斜坡AD 的坡比为1:1.2,斜坡 BC 的坡比为1: 0.8,现测得放水前的水面宽 EF 为 3.8米,当水闸放水后,水渠内水面宽GH 为6米,则放水后水面上升的高度是( )
 A、1.2 米 B、1.1 米 C、0.8米 D、2.2 米
A、1.2 米 B、1.1 米 C、0.8米 D、2.2 米 -
3、 某小区门口安装了曲臂遥控连杆道闸,如图①,连杆主要由主动杆和辅助杆两部分组成.如图②所示为遥控连杆在某次升起时的示意图,OB 为主动杆,AB 为辅助杆,OA 是指连杆处在水平静止状态时,此时点O,B,A 在同一直线上,OA∥DE(DE 表示地平线),现测得整个连杆的长度OA=4.5m ,桩的高度OE=1m . B 是 OA的三等分点(OB>AB),在升起过程中,辅助杆A'B'始终平行于地平线,连杆在完全升起后的倾角 求:
 (1)、 OB 的长度.(2)、连杆在完全升起后辅助杆A'B'距离地面的高度(参考数据: 0.17,tan80°≈5.67).
(1)、 OB 的长度.(2)、连杆在完全升起后辅助杆A'B'距离地面的高度(参考数据: 0.17,tan80°≈5.67). -
4、 如图,斜坡AB 的长为100m,坡角∠ABC=30°,现因“改小坡度”工程的需要,将斜坡AB改造成坡比为1:5 的斜坡 BD(A,D,C 三点在地面的同一条垂线上),那么由点 A 到点D 下降了m.

-
5、 如图,扇形 AOB 的半径OA=2,弦 AB =2 , 则. 的长为.

-
6、如图,某地修建一座高为5m 的天桥,如果斜坡AB 的坡比为1: , 那么斜坡AB 的长为( )
 A、10m B、 C、5m D、
A、10m B、 C、5m D、 -
7、
【定义学习】
定义:如果四边形有一组对角为直角,那么我们称这样的四边形为“对直四边形”.
【判断尝试】
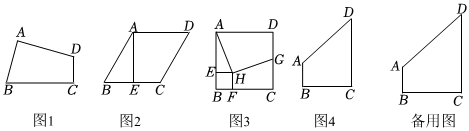
(1)、在①平行四边形②矩形③菱形④正方形中,是“对直四边形”的是;(填序号)(2)、如图1,四边形ABCD是对直四边形,若 , , , , 则边BC的长是;(3)、【操作探究】如图2,在菱形ABCD中,AB=6,∠B=60°,AE⊥BC于点E , 请在边CD上找一点F , 使得以点A、E、C、F组成的四边形为“对直四边形”,直接写出EF的长是;
(4)、【拓展延伸】如图3,在正方形ABCD中,AB=6,点E、F、G分别从点B、B、C同时出发,并分别以每秒1、1、2个单位长度的速度,分别沿正方形的边BA、BC、CD方向运动(保持CG≤CD),再分别过点E、F作AB、BC的垂线交于点H , 连结AH、HG.
试说明:四边形AHGD为对直四边形.
(5)、【实践应用】某加工厂有一批四边形板材,形状如图4所示,其中AB=2米,BC=6米,∠B=∠C=90°,∠D=45°.现根据客户要求,需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形”板材,且这两个等腰三角形的腰长相等,要求材料充分利用无剩余.请直接写出分割后得到的等腰三角形的腰长是.
-
8、阅读材料,并解决问题.
【学习研究】我国古代数学家赵爽在其所著的《勾股圆方图注》中记载了一元二次方程的几何解法,以x2+2x-35=0为例,构造方法如下:
首先将方程x2+2x-35=0变形为x(x+2)=35,然后画四个长为x+2,宽为x的矩形,按如图1所示的方式拼成一个“空心”大正方形,则图1中大正方形的面积可表示为(x+x+2)2 , 还可表示为四个矩形与一个边长为2的小正方形面积之和,即4x(x+2)+22=4×35+4.因此,可得新方程(x+x+2)2=144.因为x表示边长,所以2x+2=12,即x=5.遗憾的是,这样的做法只能得到方程的其中一个正根.
【理解应用】参照上述图解一元二次方程的方法,请在下面三个构图中选择能够用几何法求解方程x2-4x-12=0(x>0)的正确构图是.(从序号①②③中选择)
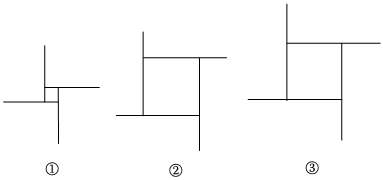
【类比迁移】小颖根据以上解法解方程2x2+3x-2=0,请将其解答过程补充完整:
第一步:将原方程变形为 , 即x()=1;
第二步:利用四个全等的矩形构造“空心”大正方形;
第三步:根据大正方形的面积可得新的方程 , 解得原方程的一个根为;
【拓展应用】一般地,对于形如x2+ax=b的一元二次方程可以构造图2来解.已知图2是由四个面积为3的相同矩形构成,中间围成的正方形面积为4,那么此方程的系数a= , b= , 求得方程的正根为.

-
9、如图,在▱ABCD中,对角线AC , BD交于点O , 点E , F分别是OB , OD的中点,连接AE、CE、AF、CF.
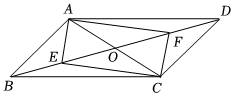 (1)、求证:四边形AECF是平行四边形;(2)、若四边形AECF是矩形,∠BAC=90°, , 求BC的长;(3)、尺规作图:过点B作直线BP , 使得BP∥AE.(保留作图痕迹,不写作法.)
(1)、求证:四边形AECF是平行四边形;(2)、若四边形AECF是矩形,∠BAC=90°, , 求BC的长;(3)、尺规作图:过点B作直线BP , 使得BP∥AE.(保留作图痕迹,不写作法.) -
10、如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,0),B(0,1),C(-2,3).
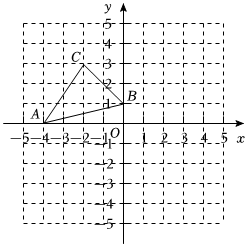 (1)、若△ABC经过平移后得到△A1B1C1 , 已知点B的对应点B1的坐标为(5,-2),请画出△A1B1C1;(2)、将△ABC绕坐标原点O按顺时针方向旋转90°得到△A2B2C2 , 请画出△A2B2C2;(3)、若将△A2B2C2绕点P旋转可得到△A1B1C1 , 则点P的坐标为 ▲
(1)、若△ABC经过平移后得到△A1B1C1 , 已知点B的对应点B1的坐标为(5,-2),请画出△A1B1C1;(2)、将△ABC绕坐标原点O按顺时针方向旋转90°得到△A2B2C2 , 请画出△A2B2C2;(3)、若将△A2B2C2绕点P旋转可得到△A1B1C1 , 则点P的坐标为 ▲ -
11、先化简: , 再从-2、-1、0、1、2中选择一个合适的数作为n的值代入求值.
-
12、解下列方程:(1)、(x-2)2=9;(2)、.
-
13、如图,在四边形ABCD中,∠BAD=45°,∠BCD=90°,连接BD、CA , 若CA平分∠BCD , , BC=5,则BD= .

-
14、在研究物体的放射性衰变时,我们常常关注放射性物质质量随时间的变化.假设在2023年初,有一块质量为500克的某种放射性同位素.由于放射性衰变,其质量会逐年减少.到2025年初,经过精确测量,该放射性同位素的质量降至405克.设这种放射性同位素质量的年平均减少率为x , 根据题意,可列出一元二次方程为:.(只列方程,不需求解)
-
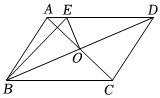
15、如图,▱ABCD的周长为60cm , AC , BD相交于点O , EO⊥BD交AD于点E , 则△ABE的周长为cm.
-
16、如图,边长为8的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC将线段EC绕点C逆时针旋转60°得到FC , 连接DF , 则在点E运动过程中,DF的最小值是( )
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1 -
17、初中毕业前夕,某数学学习兴趣小组的成员互赠纪念卡片作为毕业礼物.小组里每两名成员之间互相赠送一张卡片(即A送给B一张,B也送给A一张).已知全组共赠送了306张卡片,则该小组一共有多少名成员?( )A、16 B、17 C、18 D、19
-
18、若α,β是方程x2+2x-2025=0的两个实数根,则α2+3α+β的值为( )A、2023 B、2027 C、-2023 D、4050
-
19、如图,在一个对边平行的纸条上有两点A , B及线段AB的中点O , 以下操作和判断不正确的是( )
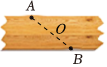 A、过点O作任意直线(除直线AB)交纸条两边于点C , D , 得到平行四边形ACBD B、过点O作AB的垂线l交纸条两边于点C , D , 得到菱形ACBD C、分别过点A , B作对边的垂线,交对边于点C , D , 得到矩形ACBD D、在点A , B所在边的对边分别取C , D两点,使得AC=BD , 得到平行四边形ACBD
A、过点O作任意直线(除直线AB)交纸条两边于点C , D , 得到平行四边形ACBD B、过点O作AB的垂线l交纸条两边于点C , D , 得到菱形ACBD C、分别过点A , B作对边的垂线,交对边于点C , D , 得到矩形ACBD D、在点A , B所在边的对边分别取C , D两点,使得AC=BD , 得到平行四边形ACBD -
20、下列等式,从左到右的变形,属于因式分解的是( )A、6x2y3=2x2•3y3 B、a(a+1)(a-1)=a3-a C、 D、.