-
1、抛物线上部分点的横坐标x , 纵坐标y的对应值如表:
x
…
0
1
2
…
y
…
5
0
…
从表中可知,下列说法中正确的是( ).
A、抛物线的对称轴是y轴 B、抛物线与x轴的一个交点为 C、函数的最小值为5 D、当时,y随x增大而减小 -
2、关于x的二次函数的图象下列说法不正确的是( )A、对称轴为直线 B、当时,图象上的最低点为 C、当时,y的值随x值的增大而增大 D、顶点一定在函数的图象上
-
3、下列关于二次函数的图象和性质的叙述中,正确的是( )A、与直线有两个交点 B、开口方向向上 C、对称轴是直线 D、点在函数图象上
-
4、已知二次函数 .
 (1)、求它的图象的顶点坐标和对称轴;(2)、画出它的图象.并结合图象,当时,则y的取值范围是 ▲ .
(1)、求它的图象的顶点坐标和对称轴;(2)、画出它的图象.并结合图象,当时,则y的取值范围是 ▲ . -
5、已知二次函数 , 完成下列各题:
 (1)、将函数关系式用配方法化为的形式,并写出它的顶点坐标、对称轴.(2)、求出它的图象与x轴的交点坐标.(3)、在直角坐标系中,画出它的图象.(4)、当为x何值时,函数y随着x的增大而增大?(5)、根据图象说明:当x为何值时,
(1)、将函数关系式用配方法化为的形式,并写出它的顶点坐标、对称轴.(2)、求出它的图象与x轴的交点坐标.(3)、在直角坐标系中,画出它的图象.(4)、当为x何值时,函数y随着x的增大而增大?(5)、根据图象说明:当x为何值时, -
6、在同一平面直角坐标系中,画出下列函数的图象:

①;②;③;④ .
从图象对比,说出解析式中二次项系数对抛物线的形状有什么影响?
-
7、在二次函数中,当时,y的取值范围是( )A、 B、 C、 D、
-
8、用配方法将二次函数化为的形式为( )A、 B、 C、 D、
-
9、/span>、为响应党中央关于打好精准扶贫攻坚战的号召,东部帮助西部进行扶贫产业开发,“食良品”是某市农产品商贸集团有限公司旗下的“消费扶贫”的电商平台,依托地理、集团专业等渠道的优势,基地直采,降低采购成本,全心全意为全市广大客户提供优质的食材,也解决了西部各地农副产品销售难的问题.目前,该平台为广大客户仅提供300元、500元、800元、1000元四种不同面额的提货券.随机抽查了其中100天的销售情况,整理统计后得到如下表一和表二:
表一
提货券每张面额(元)
300
500
800
1000
销售量(张)的百分比
30%
m%
18%
12%
表二
日均销售量(张)
300
450
500
650
天数
25
30
35
10
(1)、随机抽取一张提货券,面额不少于800元的概率是多少?(2)、哪种面额的提货券应多提供些?估计日均销售该面额的提货券多少张?(3)、估计月销售总额是多少元?(月以30天计算) -
10、/span>、某著名景区计划在西峰修建安装至多4条索道接送游客,过去10年景区游客统计资料显示,景区每年游客客流量都在160万人以上.过去10年的游客客流量的统计情况绘制成如下频数分布直方图(数据包括左端点,不含右端点,假设每年游客客流量不相互影响).
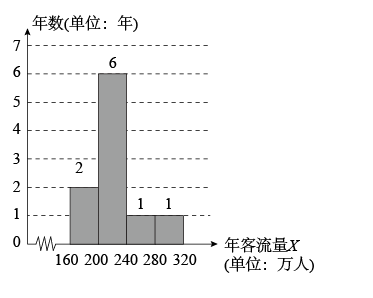
以过去10年的游客客流量的统计情况为参考依据.
(1)、求该景区今年游客客流量不低于240万人的概率;(2)、若该景区希望安装的索道尽可能运行,但每年索道最多可运行条数受游客客流量的限制,并有如下表关系:年游客客流量(单位:万人)
索道最多可运行条数
1
2
3
4
若某条索道运行,则该条索道年利润为6000万元;若某条索道未运行,则该条索道年亏损2000万元,从平均获利的角度看,帮景区作出决策,应选择安装2条还是3条索道获利较多?请说明理由.
-
11、/span>、为鼓励学生积极加入中因共青团组织,某学校团委在八、九年级各抽取50名学生开展团知识竞赛,为便于统计成绩,制定了取整数的计分方式,满分10分.竞赛成绩如图所示:
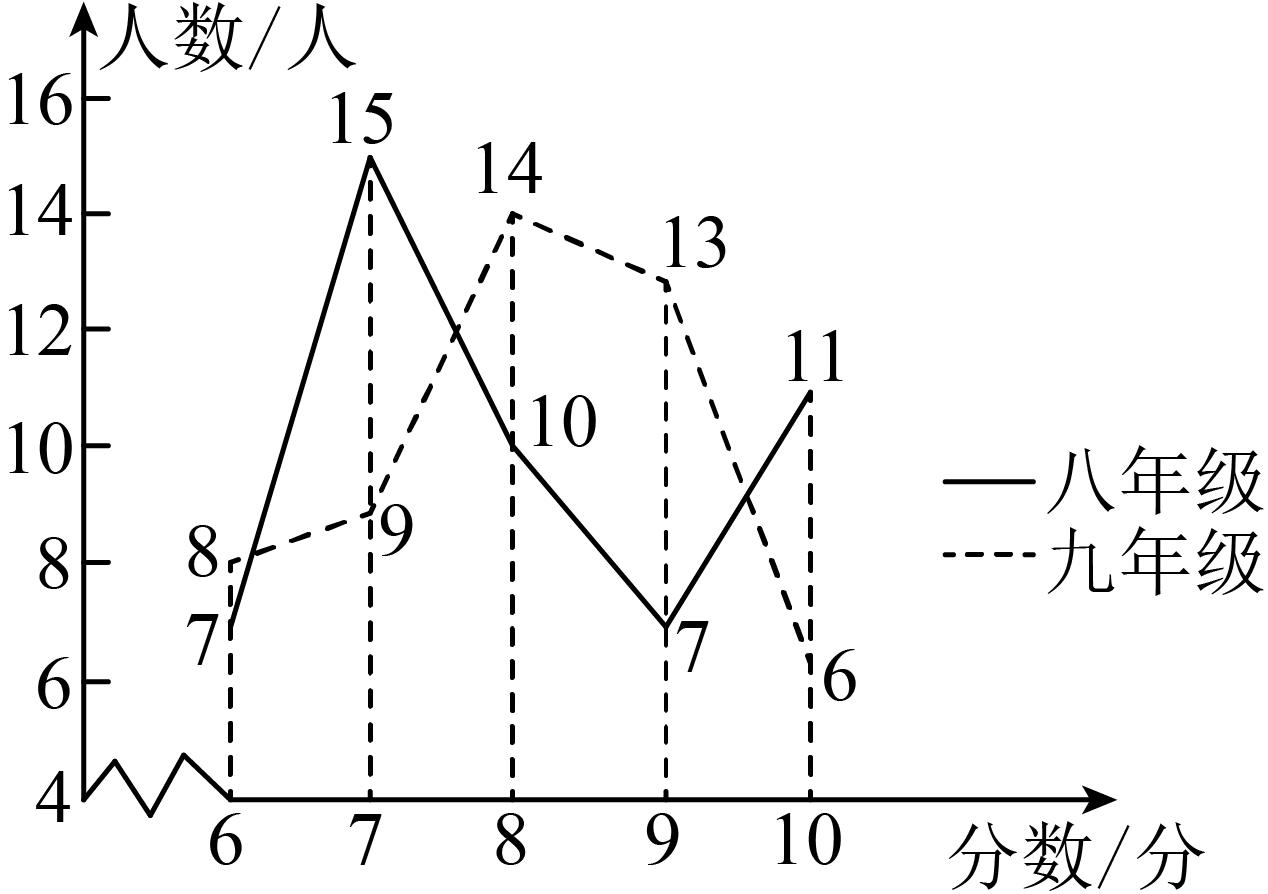
平均数
众数
中位数
方差
八年级
8
7
九年级
8
8
(1)、请根据图表中的信息,回答下列问题.①表中的 ▲ , ▲ , ▲ ;
②现要给成绩突出的年级颁奖,如果从方差的角度来分析,你认为应该给哪个年级颁奖?
(2)、若规定成绩10分获一等奖,9分获二等奖,8分获三等奖,请通过计算说明哪个年级的获奖率高? -
12、/span>、在数学实践活动课上,小明和小红玩转盘游戏,分别转动如下的两个转盘(每个转盘都被分成3等份)
 (1)、转动转盘①时,该转盘指针指向“3”的概率是;(2)、若同时转动两个转盘,规定:转盘停止指针指向的两个数字之和为奇数时小明获胜;两个数字之和为偶数时小红胜,你觉得此游戏对双方是否公平?请说明理由.
(1)、转动转盘①时,该转盘指针指向“3”的概率是;(2)、若同时转动两个转盘,规定:转盘停止指针指向的两个数字之和为奇数时小明获胜;两个数字之和为偶数时小红胜,你觉得此游戏对双方是否公平?请说明理由. -
13、2024贵阳马拉松比赛于6月16日上午7点30分在贵阳国际会展中心北广场正式鸣枪起跑,本届马拉松赛共设置四个项目,分别是马拉松、半程马拉松、迷你马拉松以及线上马拉松.经过大家积极的参与,报名人数共计93902人,由于场地人数限制,需要抽签决定是否能够参与比赛.小红和小星类比该方式进行抽签决定是否参加某场活动,在一个不透明的袋子中放入4个完全一样的小球,分别标有1、2、3、4四个数字,小红和小星轮流从袋中摸出一球,记下号码,然后放回.(1)、计算摸到小球数字为2的概率;(2)、如果摸到的球号码大于2,则小红参加活动,否则小星参加活动,你认为这个抽签方式公平吗?请说明理由.
-
14、/span>、有两个可以自由转动的均匀转盘A , B . 转盘A被平均分成4等份,分别标上 , 2,6,8四个数字;转盘B被平均分成3等份,分别标上 , , 3三个数字.自由转动转盘A与B , 转盘停止后,指针各指向一个数字(指向分界线时重新转),把A转盘指的数字作为被除数,B转盘指针指的数字作为除数,计算这两个数的商.小贝和小晶用以上两个转盘做游戏,规则是:若这两数的商为负整数,则小贝赢;若这两个数的商为正数,则小晶赢.你认为该游戏公平吗?请你用画树状图或列表的方法,说明是否公平;如果不公平,请你修改游戏规则,使游戏公平.
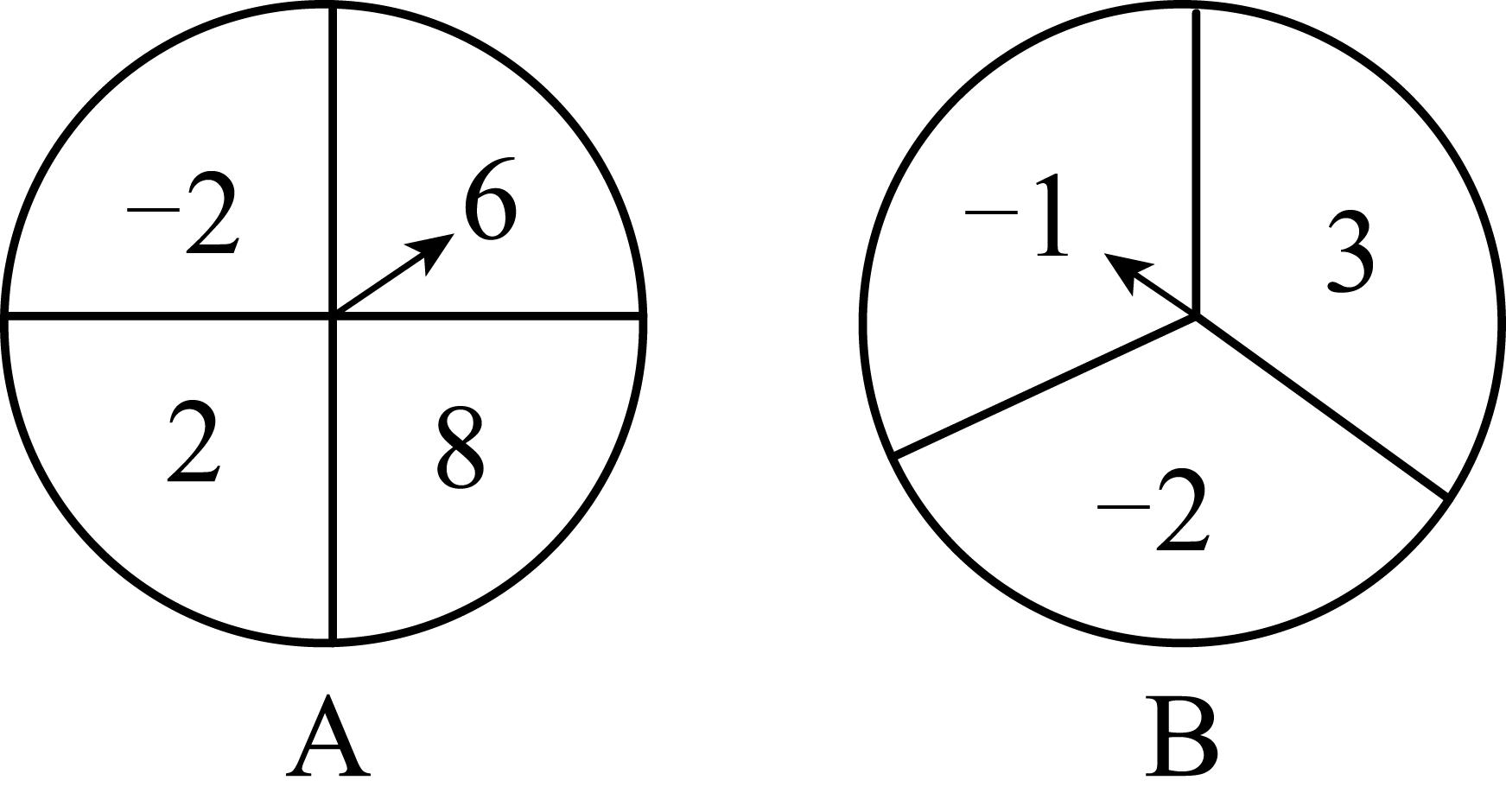
-
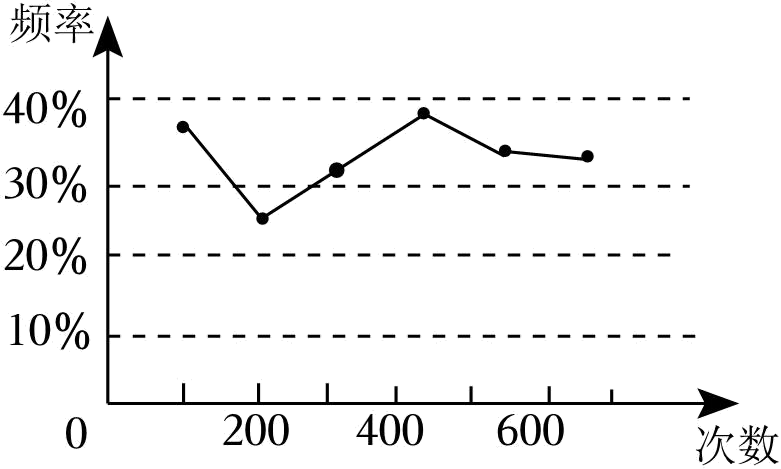
15、七(1)班同学设计用频率去估计概率的试验如下:在一个不透明的口袋中,装有6个球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球试验,统计了黄球出现的次数,绘出的统计图如图所示,则袋子中黄球的个数最可能是个.
-
16、/span>、在一次大量重复试验中,统计了某一结果出现的频率.绘制出的统计图如图所示,符合这一试验结果的可能是( )
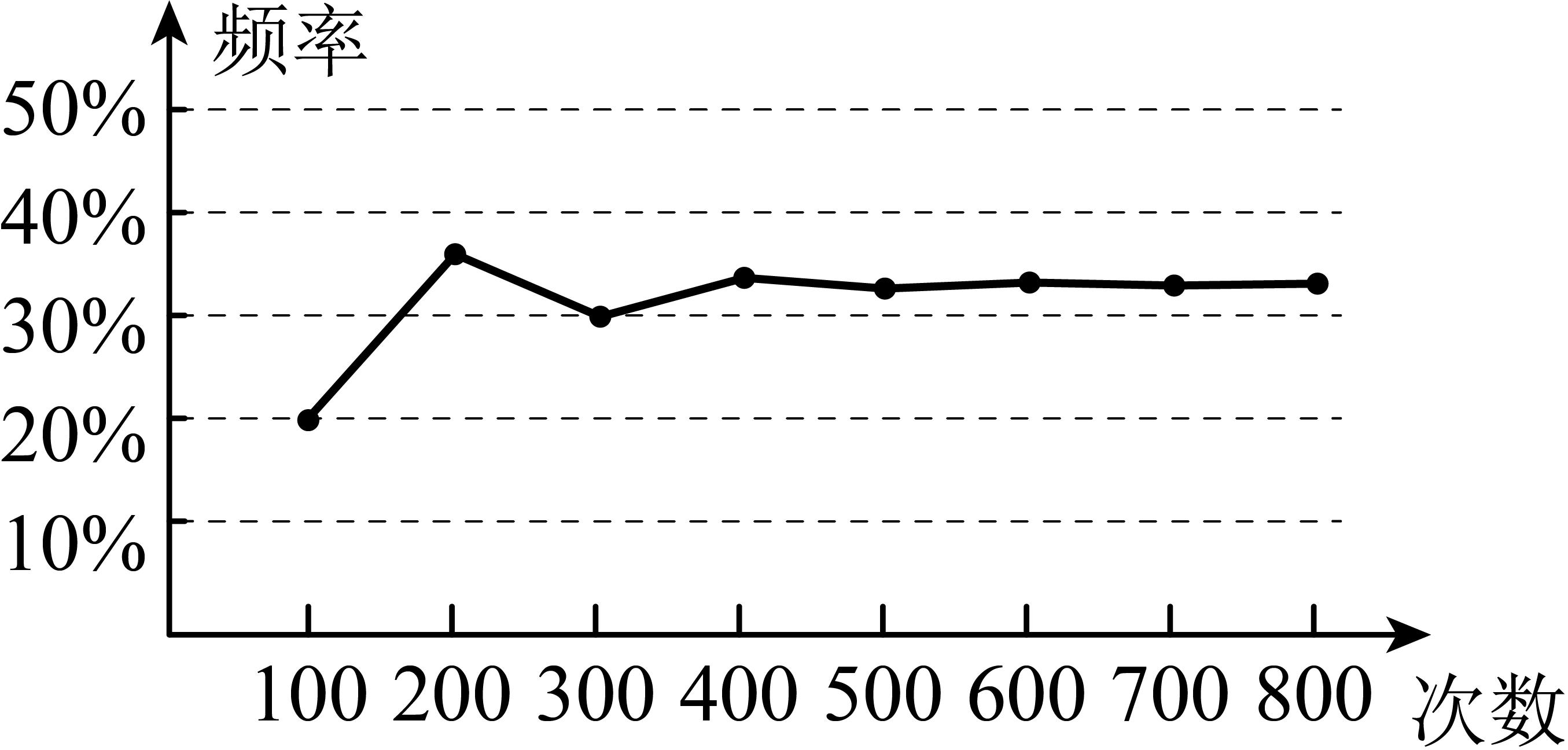 A、掷一枚质地均匀的骰子,出现2点朝上 B、从一个装有大小相同的2个蓝球和1个白球的不透明袋子中随机取一球,取到白球 C、抛一枚1元钱的硬币,出现反面朝上 D、从标有数字1到10的十张大小相同的纸牌中随机抽取一张,是奇数
A、掷一枚质地均匀的骰子,出现2点朝上 B、从一个装有大小相同的2个蓝球和1个白球的不透明袋子中随机取一球,取到白球 C、抛一枚1元钱的硬币,出现反面朝上 D、从标有数字1到10的十张大小相同的纸牌中随机抽取一张,是奇数 -
17、/span>、一只不透明的袋中装有除颜色外都相同的红球、黄球、白球共50个.通过多次摸球试验后,发现摸到红球、黄球的频率分别是 . 则可估计袋中白球的个数是( )A、10 B、15 C、25 D、20
-
18、/span>、都相同.将袋中小球摇匀,从中随机摸出一个小球记下颜色后放回,记作随机摸球一次.(1)、随机摸球10次,其中摸出黄球3次,则这10次摸球中,摸出黄球的频率是 .(2)、随机摸球2次,用画树状图或列表的方法,求这两次摸出的小球都是红球的概率.
-
19、/span>、近日,甘肃天水这座历史悠久的文化古城,因一碗麻辣烫而迅速走红网络,成为旅游新热点.自天水火爆“出圈”以来,各级团组织迅速行动起来,全面承担起志愿服务工作,同时带领一大批青年志愿者积极响应团组织号召投入志愿服务工作.根据实际需要,志愿者被陆续分配到四合院美味城网红麻辣烫店、机场、火车站等区域开展志愿服务工作.某段时间内经过抽样调查,发现志愿者服务的区域主要有A , B , C , D , E五个.抽样调查的统计结果如下表, 则下列说法不正确的是( )
区域
A
B
C
D
E
人数
A、去区域服务的人数最少 B、去区域服务的人数的频率是 C、若有名志愿者参与服务,则约有人被分配到C区域服务 D、这次抽样调查的样本容量是 -
20、/span>、调查某班 名同学的跳高成绩时,在收集到的数据中,不足 米的数出现的频率是 , 则达到或超过 米的数出现的频率是 ( )A、 B、 C、 D、