-
1、观察表格,估算一元二次方程的近似解:
x
1.4
1.5
1.6
1.7
1.8
0.19
0.44
由此可确定一元二次方程.的一个近似解x的范围是( )
A、 B、 C、 D、 -
2、已知抛物线 上的某些点的横坐标x与纵坐标y的对应值如下表:
x
y
则该函数与x轴的其中一个交点的横坐标的范围是( )
A、 B、 C、 D、 -
3、如图,已知拋物线经过 , , 三点,直线是拋物线的对称轴,点M是直线上的一个动点,当最短时,点M的坐标为 .

-
4、如图,抛物线与轴交于两点,与轴交于点 , 点是抛物线的对称轴上一动点,连接和 , 则的最小值是 .

-
5、已知 , 是抛物线上的两点,则正数( )A、2 B、4 C、8 D、
-
6、已知二次函数 , 当时,x的取值范围是 , 且该二次函数的图象经过点 , 两点,则d的值不可能是( )A、 B、4 C、 D、6
-
7、在平面直角坐标系中,二次函数的图象经过点和点 , 其顶点在轴上,则的值为( )A、4 B、8 C、12 D、16
-
8、对于二次函数 的性质,下列描述正确的是( )A、开口向下 B、对称轴是直线 C、顶点坐标是 D、抛物线可由向右平移1个单位得到
-
9、把抛物线向左平移1个单位,然后向上平移2个单位,则平移后抛物线的表达式是( )A、 B、 C、 D、
-
10、将抛物线向左平移3个单位长度得到抛物线( )A、 B、 C、 D、
-
11、已知二次函数的图象如图所示.
 (1)、求这个二次函数的解析式;(2)、根据图象回答:当时,的取值范围;(3)、当时,求的取值范围.
(1)、求这个二次函数的解析式;(2)、根据图象回答:当时,的取值范围;(3)、当时,求的取值范围. -
12、已知抛物线的顶点坐标为 , 与轴的交点坐标为 , 求此抛物线对应的函数表达式.
-
13、已知二次函数 .(1)、求证:该函数的图象与轴总有两个公共点;(2)、若该函数图象与轴的两个交点坐标分别为 , , 且 , 求证:;(3)、若 , , 都在该二次函数图象上,且 , 结合函数图象,写出的取值范围是 .
-
14、已知关于x的二次函数(1)、若该函数的图象与x轴的交点坐标是 , 求的值;(2)、若该函数的图象的顶点纵坐标为3,
①用含b的代数式表示c;
②当时,y的取值范围是 , 求c的取值范围.
-
15、已知二次函数的图象与y轴相交于点 .(1)、若 , 求该二次函数的最小值;(2)、若 , 点都在该函数的图象上,比较和的大小关系;(3)、若点都在该二次函数图象上,分别求的取值范围
-
16、已知二次函数的图象如图所示,则一次函数的图象大致为( )
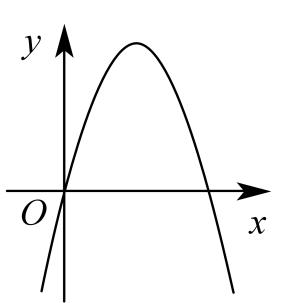 A、
A、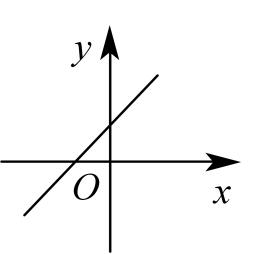 B、
B、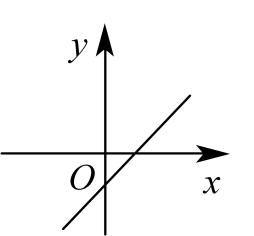 C、
C、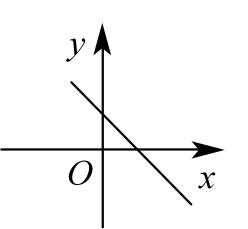 D、
D、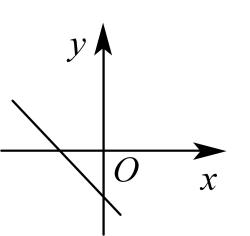
-
17、如图,已知二次函数的图象与轴交于点 , 与轴的交点在和之间(不包括这两点),对称轴为直线 , 下列结论:①;②;③;④;其中正确结论的个数有( )
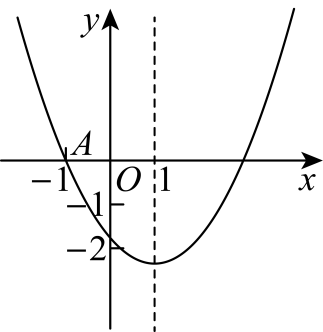 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
18、如图,二次函数( , , 为常数,)的图象与轴交于点 , 对称轴是直线 , 有以下结论:①;②若点和点都在抛物线上,则;③(为任意实数);④ . 其中正确的有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
19、二次函数的自变量(表格中从左到右增大)与函数值的对应值如下表:
0
1
3
1
0
1
下列判断正确的是( )
A、 B、 C、 D、 -
20、用描点法画二次函数的图象时,列出了下面的表格:
从表中信息可得值为( )
A、 B、 C、 D、