相关试卷

1、对于任意非负整数 $p$ ， $a$ ， $b$ 若满足： $p = a^{2} - b^{2}$ ，则称 $p$ 为 $a$ 与 $b$ 的“2次幂差数”．

(1)、下列两个数：① $8$ ， ② $6$ ，其中不是“2次幂差数”的是______(填序号)；

(2)、若 $p$ 为 $a$ 与 $b$ 的“2次幂差数”，且 $b$ ， $a$ 是两个连续的正整数，证明： $p$ 为奇数；

(3)、若 $p$ 为 $a$ 与 $b$ 的“2次幂差数”，且 $b = k - 3$ ， $p = - 2 k + 71$ ，求 $a$ 的最小值．

查看解析
2、如图，在 $6 \times 6$ 的正方形网格中， $△ A B C$ 的三个顶点都在格点上，请使用无刻度直尺按要求作图．（注意先用铅笔画，再用水笔描，求作的图形用实线，辅助的线条用虚线）

(1)、在图1中，画出 $A B$ 边上的高 $C D$ ；

(2)、在图2中，画出 $A C$ 边上的中线 $B E$ ；

(3)、在图3中，画 $△ A B F$ ，使 $△ A B F$ 与 $△ A B C$ 全等（F不与C重合，画出一个即可）．

查看解析
3、为进一步发展新质生产力，某企业计划对现有甲、乙两类生产线的设备进行更新换代，经测算，升级1条甲类生产线比升级 $1$ 条乙类生产线需多投入 $5$ 万元，用 $120$ 万元升级甲类生产线的条数和用 $100$ 万元升级乙类生产线的条数相同，设升级 $1$ 条乙类生产线需投入 $x$ 万元．

(1)、升级 $1$ 条甲类生产线需投入______万元，用 $120$ 万元升级甲类生产线的条数为______条；(用含 $x$ 的式子表示)

(2)、升级一条甲类、乙类生产线各需投入多少资金？

查看解析
4、如图，点A，D，B，E在一条直线上， $A C = D F$ ， $A D = B E$ ， $∠ A = ∠ E D F$ ，求证： $∠ C = ∠ F$ ．

查看解析
5、先化简，再求值： $(1 + \frac{3}{x - 1}) \div \frac{x^{2} - 4}{x - 1}$ ，其中 $x = 3$ ．

查看解析
6、化简：

(1)、 $(a - b) (a + 2 b)$ ；

(2)、 $(2 x^{3} y^{2} - 6 x^{2} y) \div 2 x y$ ．

查看解析
7、如图， $△ A B C$ 中， $A C = B C$ ， $B E ⊥ A C$ ， E为垂足，点D在 $B C$ 上，且 $A B = A D$ ，若 $C E = 3 C D$ ， $A E = 2$ ，则 $B C$ 的长为．

查看解析
8、如图，两个正方形放置于长方形 $E F G H$ 内（正方形的两边在长方形的边上），长方形 $A B C D$ 是两正方形的重叠部分，已知阴影部分①与阴影部分②的周长之差为m，面积之差为n，则 $A B + H G =$ （用含m、n的代数式表示）．

查看解析
9、如图， $△ A B C$ 中， $A B = A C$ ， $∠ B = 75 °$ ，过点 $A$ ，点 $C$ 分别作 $A B$ ， $A C$ 的垂线相交于点 $D$ ，则 $\frac{A B}{A D} =$ ．

查看解析
10、若分式 $\frac{a - 2}{a^{2} + 1}$ 的值为零，则 $a =$ ．

查看解析
11、如图，正方形 $A B C D$ 是由四个全等的直角三角形和小正方形 $E F G H$ 拼成，连接 $A C$ ， $E C$ ，若想求出图中阴影部分的面积，只需知道（）

A、 $A B$ 的长 B、 $A E$ 的长 C、 $E F$ 的长 D、 $C E$ 的长

查看解析
12、若实数 $a$ ， $b$ ， $c$ 满足 $b - c = 2$ ， $a^{2} = - b c - 1$ ，则 $a + b + c$ 的值为( )

A、0 B、1 C、2 D、3

查看解析
13、如图， $Rt △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ， $A D$ 为 $B C$ 边上的高，E，F为 $A C$ ， $A B$ 上的点， $D E ⊥ D F$ ，若 $B F + C E = 4$ ，则 $△ A B C$ 的面积为（）

A、4 B、8 C、12 D、16

查看解析
14、点 $A (m, 5)$ 与点 $B (- m, 5)$ 关于（）对称

A、x轴 B、y轴 C、原点 D、直线x=5

查看解析
15、已知等腰三角形一边的长为3，另一边的长为7，则等腰三角形的周长为（）

A、17 B、13 C、17或13 D、无法确定

查看解析
16、如图，在 $△ A B C$ 中，点D在 $B C$ 上， $A B = A D = C D$ ， $∠ C = 40 °$ ，则 $∠ B$ 的度数为（）

A、 $40 °$ B、 $50 °$ C、 $70 °$ D、 $80 °$

查看解析
17、如图， $△ A B C ≌ △ D E F$ ， $∠ B A C = 85 °$ ， $∠ F = 40 °$ ，则 $∠ B$ 的度数为（）

A、 $85 °$ B、 $40 °$ C、 $55 °$ D、 $65 °$

查看解析
18、下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $a^{3} - a = a^{2}$ C、 ${(a^{2})}^{3} = a^{5}$ D、 ${(2 a^{2})}^{2} = 4 a^{4}$

查看解析
19、下列四幅七巧板拼成的“人形”图形中，是轴对称图形的是（）

A、握手 B、您好 C、拜托 D、谢谢

查看解析
20、【数学发现】
某校数学兴趣小组进行了如下探究：以△ABC内部任意一点O为中心，画出与△ABC成中心对称的△A^'B^'C^' ．当点O处于不同位置时，从“形”的角度发现两个三角形的重叠部分只可能有两种情况：如图1所示的平行四边形，如图2所示的有三组对边分别平行的六边形（称为“平行六边形”）；从“数”的角度发现两个三角形重叠部分的面积在不断变化．
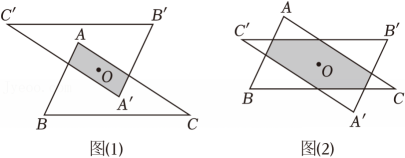
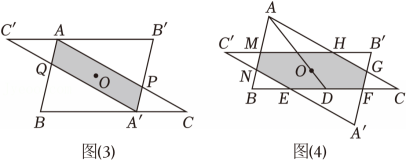
【问题解决】
组员小明选择面积为1的△ABC ，以其内部任意一点O为中心，画出与之成中心对称的△A^'B^'C^' ，探究了下列问题，请你帮他解答．

(1)、如图3，BC＝2，当点A关于点O的对称点A^'落在边BC上时，两个三角形重叠部分为▱AQA^'P ．
①若AA^'⊥BC ，求AO的长；（请直接写出答案）
②若▱AQA^'P的面积为 $\frac{1}{4}$ ，求A^'C的长．

(2)、如图4，点D为BC的中点，点O在AD上，若两个三角形的重叠部分为“平行六边形”EFGHMN ，求“平行六边形”EFGHMN面积的最大值，并指出此时点O的位置．

查看解析

上一页 193 194 195 196 197 下一页跳转