-
1、如图1是博物馆屋顶的图片,屋顶由图2中的瓦片构成,瓦片横截面如图3所示,是以点O为圆心,18cm为半径的弧,弦AB的长为18cm,则的长是( )
 A、24πcm B、12πcm C、10πcm D、6πcm
A、24πcm B、12πcm C、10πcm D、6πcm -
2、七巧板具有深厚的中华文化底蕴,它是由正方形、平行四边形和大小不一的等腰直角三角形组成的.小明用七巧板拼成的丹顶鹤如图所示,且过点C作直线AB∥DE.若∠1=20°,则∠2的度数是( )
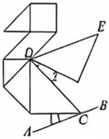 A、15° B、20° C、25° D、30°
A、15° B、20° C、25° D、30° -
3、在文创商店,小明向服务人员询问丹顶鹤、麋鹿、勺嘴鹬三种卡通饰品哪种最畅销.“最畅销”涉及的统计量是( ).A、平均数 B、中位数 C、方差 D、众数
-
4、在非物质文化遗产展区,小明看到如下发绣作品,其中作品主体图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
5、小明的背包随安检传送带移动,主要涉及的图形变换是( )A、平移 B、轴对称 C、旋转 D、位似
-
6、小明从小区﹣2楼出发,实数﹣2的绝对值是( )A、2 B、﹣2 C、 D、
-
7、【问题背景】
水火箭是一种基于水和压缩空气的简易火箭,通常由塑胶汽水瓶作为火箭的箭身,并把水当作喷射剂.图是某学校兴趣小组制做出的一款简易弹射水火箭.
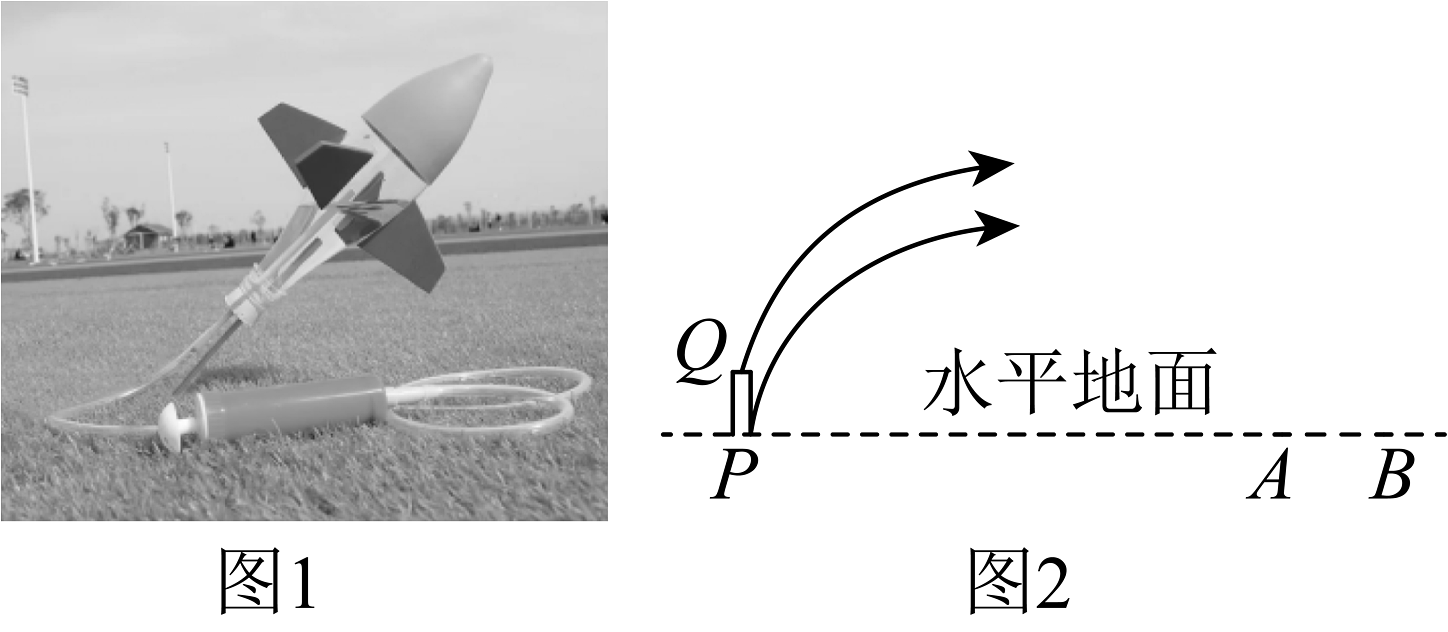
【实验操作】
为验证水火箭的一些性能,兴趣小组同学通过测试收集了水火箭相对于出发点的水平距离(单位:)与飞行时间(单位:)的数据,并确定了函数表达式为: . 同时也收集了飞行高度(单位:)与飞行时间(单位:)的数据,发现其近似满足二次函数关系.数据如表所示:
飞行时间
飞行高度
【建立模型】
任务:求关于的函数表达式.
【反思优化】
图是兴趣小组同学在室内操场的水平地面上设置一个高度可以变化的发射平台(距离地面的高度为),当弹射高度变化时,水火箭飞行的轨迹可视为抛物线上下平移得到,线段为水火箭回收区域,已知 , .
任务:探究飞行距离,当水火箭落地(高度为)时,求水火箭飞行的水平距离.
任务:当水火箭落到内(包括端点 , ),求发射台高度的取值范围.
-
8、【知识技能】
材料:若关于的一元二次方程的两个根为 , , 则 , .
材料:已知一元二次方程的两个实数根分别为 , , 求的值.
解:∵一元二次方程的两个实数根分别为 , , ∴ , ,
则 .
【数学理解】
(1)一元二次方程的两个根为 , , 则_____,______.
【拓展探索】
(2)已知一元二次方程的两根分别为 , , 求的值.
(3)已知实数 , 满足 , , 且 , 求的值.
-
9、如图,抛物线与轴相交于 , 两点,与轴相交于点 .
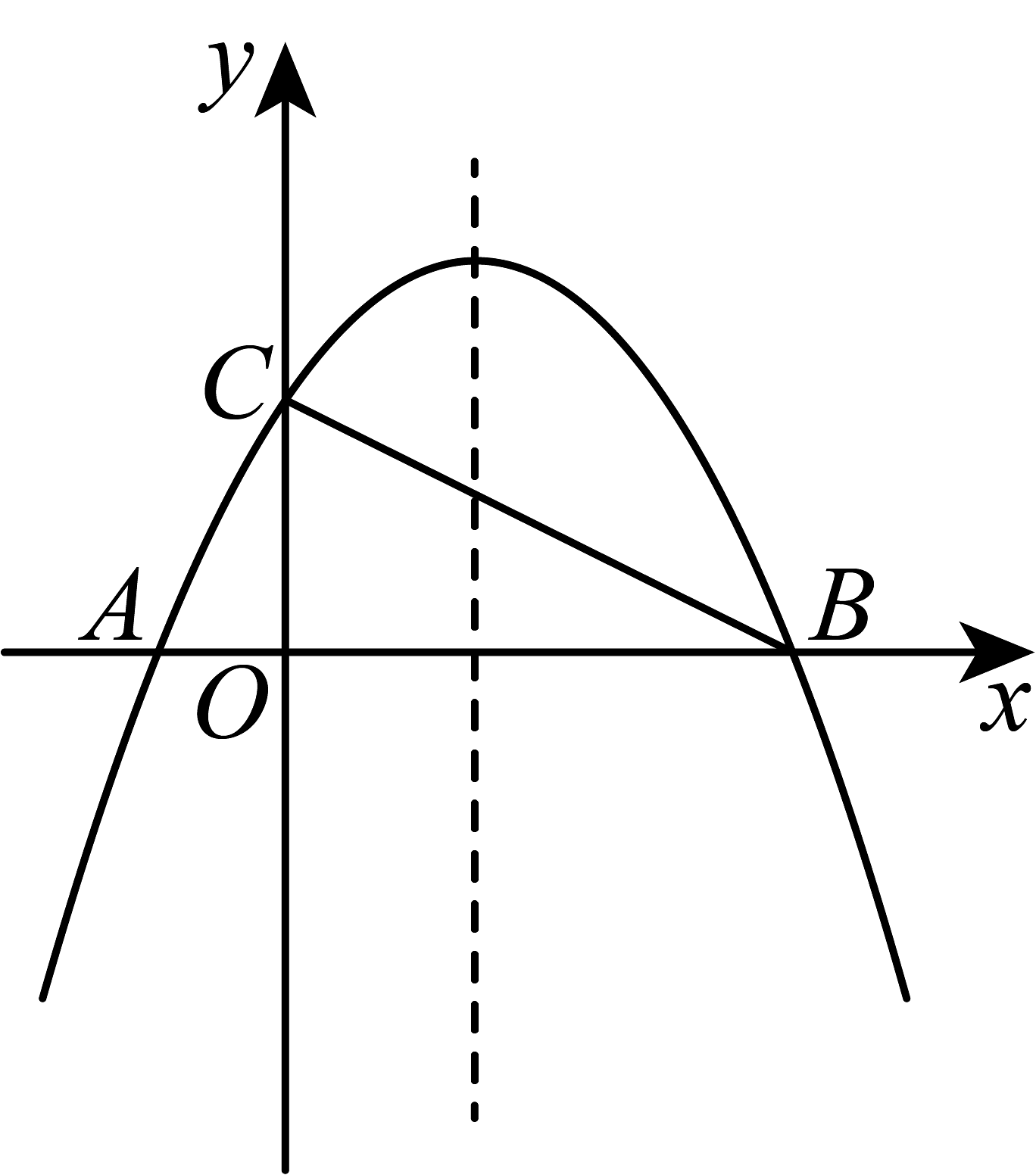 (1)、求抛物线的解析式和对称轴;(2)、利用图象回答:当取何值时, .
(1)、求抛物线的解析式和对称轴;(2)、利用图象回答:当取何值时, . -
10、如图,在平面直角坐标系中,△的顶点坐标分别为 , , .
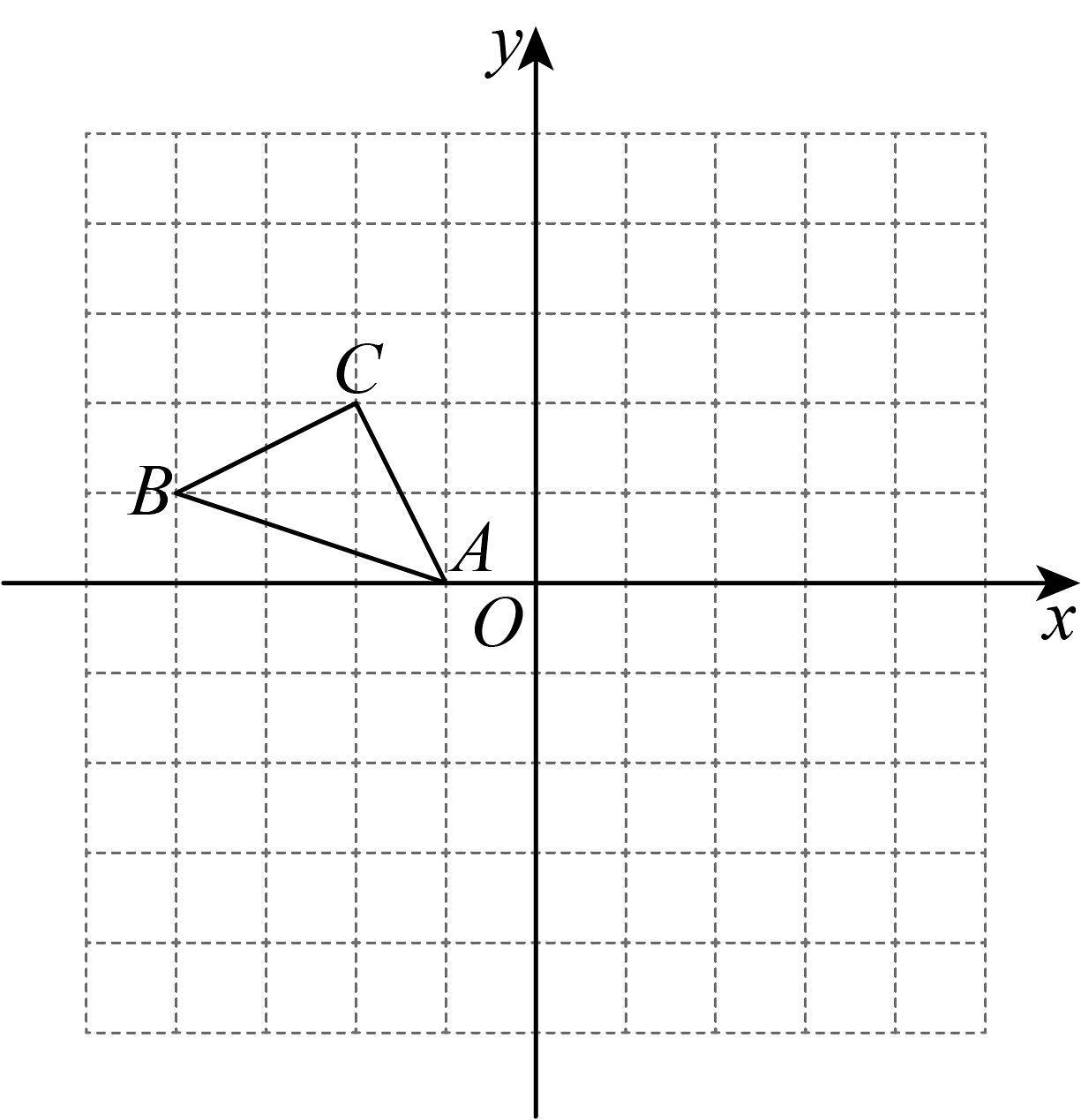 (1)、直接写出点关于轴对称的点的坐标:_____;(2)、平移△ , 使平移后点的对应点的坐标为 , 请画出平移后的△;(3)、求线段的长度.
(1)、直接写出点关于轴对称的点的坐标:_____;(2)、平移△ , 使平移后点的对应点的坐标为 , 请画出平移后的△;(3)、求线段的长度. -
11、用适当的方法解方程:(1)、;(2)、 .
-
12、要组织一次足球联赛,赛制为双循环形式(每两队之间都进行两场比赛),共要比赛90场.设共有x个队参加比赛,则x满足的关系式为 .
-
13、二次函数的最小值为 .
-
14、如图,在等边中, , 点是的中点,将绕点逆时针旋转后得到 , 那么线段的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
15、中国已经成为全球最大并且最有活力的新能源汽车市场.中国汽车工业协会数据显示,某品牌新能源汽车2022年5月份销量为10万辆,7月份销量为14.5万辆.设该品牌新能源汽车的月平均增长率为 , 则( )A、 B、 C、 D、
-
16、将小鱼图案绕着头部某点顺时针旋转90°后可以得到的图案是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
17、方程的解是( )A、 B、 C、 D、没有实数根
-
18、2024年4月,中国航天成功发射神舟十八号飞船.下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )A、
 中国探火
B、
中国探火
B、 中国火箭
C、
中国火箭
C、 中国探月
D、
中国探月
D、 中国行星探测
中国行星探测
-
19、综合实践
【活动交流】数学活动课上,周老师让学生用一段绳子(无弹性)沿着三角板的两直角边边缘拉直滑动.
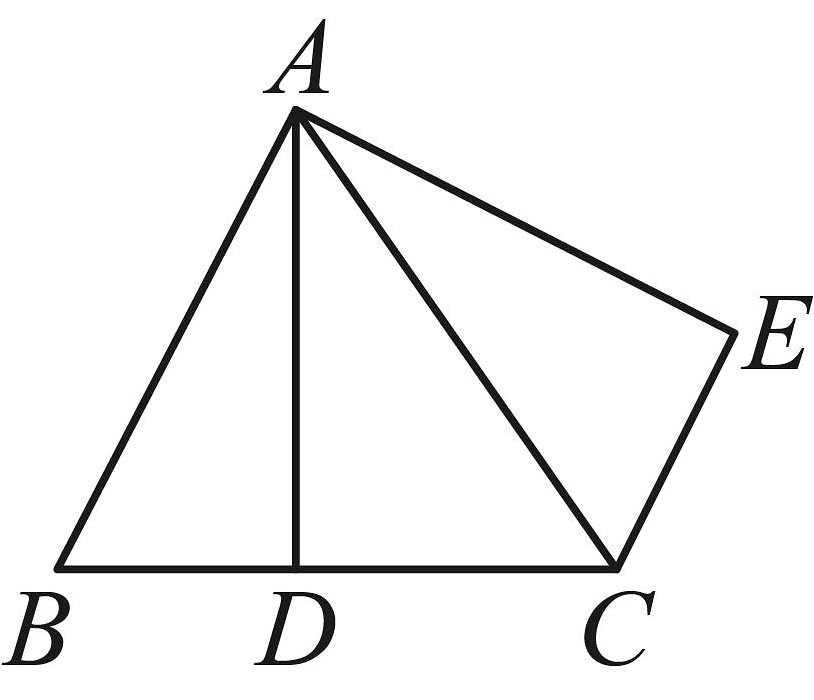
如图1,第一次拉成折线 , 且 , 第二次拉成折线 , 探究绳子两个端点之间距离的变化情况.
周老师和同学们在探究时,有如下交流:
小明:两种不同位置,绳子的两个端点的距离不一样,即 .
小聪:我发现问题可抽象为:如图 , 在中, , 在和延长线上分别取点 , , 若 , 则 .
小颖:小聪,在探究你的问题的过程中,我发现点是中点.
周老师:小聪发现的结论是正确的,当绳子两端到角顶点距离相等时,绳子两端距离最小.
结合上述师生的交流完成下面任务:
【探究论证】
(1)如图2,请你证明小颖发现的结论;
(2)如图2,请你证明小聪发现的结论;
【创新应用】
(3)如图3,中, , , , 点 , , 分别在边 , , 上,若 , 求的最小值.

-
20、(1)观察下列命题完成填空:
①若 , 则有或 ,
②若 , 则有或 ,
③若 , 则有或 ,
④若 , 则有或 ,
…
按规律猜想:若(括号内为 ),则有或______;
(2)若把(1)中命题改为:“若 , 则有或”仍然成立,猜想m,n,k应满足的等量关系式为______,并证明该命题成立;
(3)对于(2)中的m,n,k , 若满足 , 求的值.