-
1、先化简,再求值: , 已知 .
-
2、王老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,则所捂住的多项式为?

-
3、计算(1)、(2)、
-
4、在学习完《有理数》后,小奇对运算产生了浓厚的兴趣.他借助有理数的运算,定义了一种新运算“”,规则如下: . 则的值是;则的值是 .
-
5、我们平常用的数都是十进制的,如: . 表示十进制的数要用10个数码(又叫数字):0,1,2,3,4,5,6,7,8,9.电子计算机中用的二进制只有两个数码:0,1.二进制数可以转化为十进制数,如:二进制数 , 等于十进制数5;二进制数 , 等于十进制数22,那么二进制数11010等于十进制数 .
-
6、如下表所示,若A与B两个量成反比例关系,则x的值为 .
A
12
8
B
6
x
-
7、如图所示,数轴被折成 , 圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3,先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数 2019将与圆周上的数字( )重合.
 A、3 B、0 C、1 D、2
A、3 B、0 C、1 D、2 -
8、将式子中的除法转化为乘法运算,正确的是( )A、 B、 C、 D、
-
9、若 , 则代数式的值为( )A、8 B、2 C、0 D、
-
10、(1)化简:;
(2)先化简再求值: , 其中 , .
-
11、计算(1)、;(2)、;(3)、(4)、
-
12、把下列各数表示在数轴上,并用“>”连接3, , , 0, ,

-
13、观察下列各式的计算结果:
;
;
;
;
…
(1)用你发现的规律填写下列式子的结果:× .
(2)用你发现的规律计算:
.
-
14、多项式:是一个四次三项式,那么 .
-
15、若单项式与可以进行合并,则 .
-
16、已知 , , 且 , 则的值等于( )A、7和 B、7 C、和 D、以上答案都不对
-
17、据报道,2024年春节期间,泉州文旅市场共接待旅游人数818.12万人次,实现旅游收入80.18亿元,游客接待量与旅游总收入均创历史新高,用科学记数法可将数据表示为( )A、 B、 C、 D、
-
18、如图1,在中, , , 为边上任一点,连接 , 延长到 , 使 . 设 .
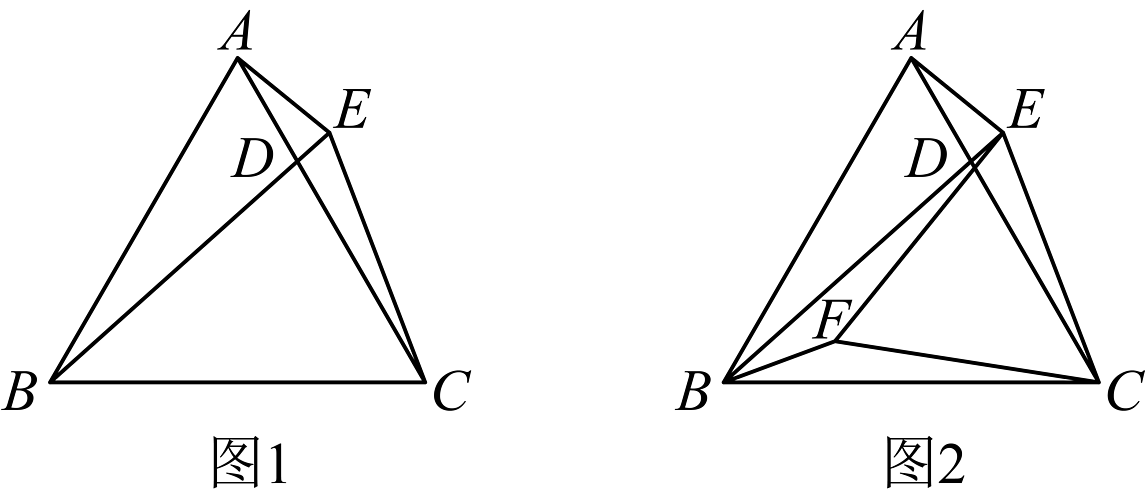 (1)、则的大小为______(用含的代数式表示);(2)、如图2,点在的平分线上,连接、 , 若 , 判断的形状并加以证明.
(1)、则的大小为______(用含的代数式表示);(2)、如图2,点在的平分线上,连接、 , 若 , 判断的形状并加以证明. -
19、如图,在 中, , 点 D是的延长线上一点,是线段的垂直平分线,交于点 F. 求证:点 E在线段的垂直平分线上.
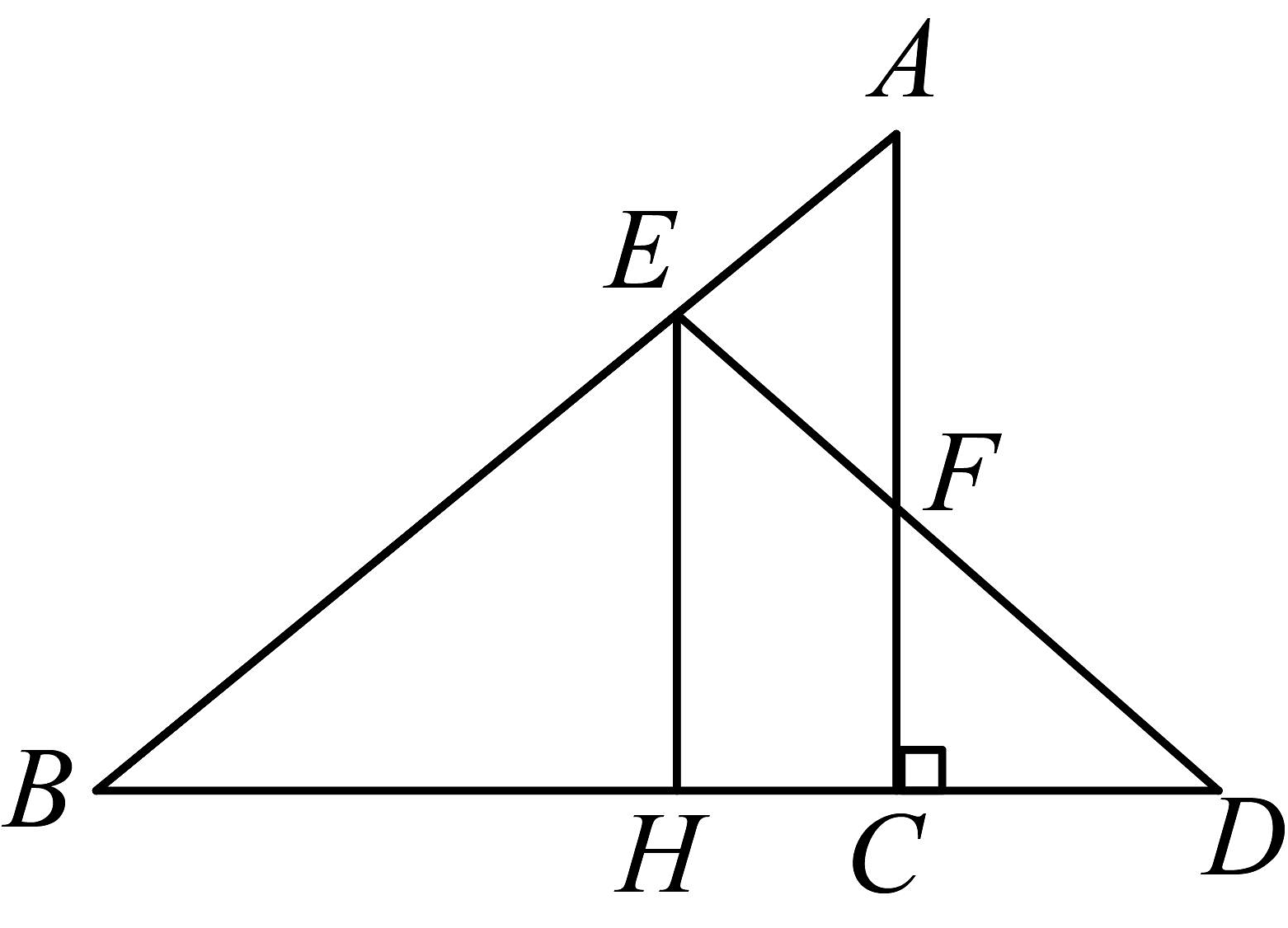
-
20、如图,在边长为1个单位长度的小正方形组成的正方形网格中,点、、在小正方形的顶点上.
 (1)、在图中画出与关于直线成轴对称的;(2)、的面积为______.(3)、在直线上确定点 , 使得最小.
(1)、在图中画出与关于直线成轴对称的;(2)、的面积为______.(3)、在直线上确定点 , 使得最小.