-
1、把下列各数表示在数轴上,并用“>”连接3, , , 0, ,

-
2、观察下列各式的计算结果:
;
;
;
;
…
(1)用你发现的规律填写下列式子的结果:× .
(2)用你发现的规律计算:
.
-
3、多项式:是一个四次三项式,那么 .
-
4、若单项式与可以进行合并,则 .
-
5、已知 , , 且 , 则的值等于( )A、7和 B、7 C、和 D、以上答案都不对
-
6、据报道,2024年春节期间,泉州文旅市场共接待旅游人数818.12万人次,实现旅游收入80.18亿元,游客接待量与旅游总收入均创历史新高,用科学记数法可将数据表示为( )A、 B、 C、 D、
-
7、如图1,在中, , , 为边上任一点,连接 , 延长到 , 使 . 设 .
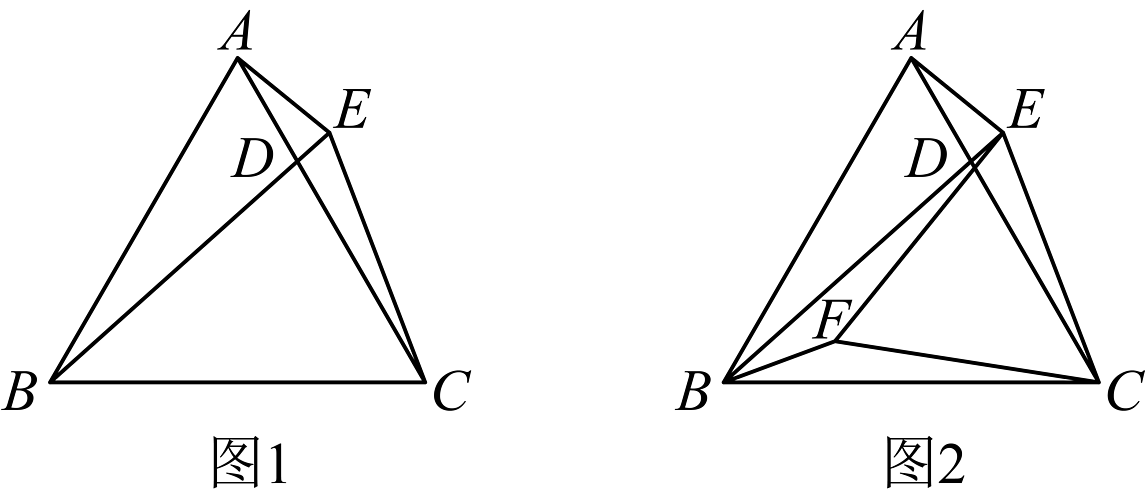 (1)、则的大小为______(用含的代数式表示);(2)、如图2,点在的平分线上,连接、 , 若 , 判断的形状并加以证明.
(1)、则的大小为______(用含的代数式表示);(2)、如图2,点在的平分线上,连接、 , 若 , 判断的形状并加以证明. -
8、如图,在 中, , 点 D是的延长线上一点,是线段的垂直平分线,交于点 F. 求证:点 E在线段的垂直平分线上.
-
9、如图,在边长为1个单位长度的小正方形组成的正方形网格中,点、、在小正方形的顶点上.
 (1)、在图中画出与关于直线成轴对称的;(2)、的面积为______.(3)、在直线上确定点 , 使得最小.
(1)、在图中画出与关于直线成轴对称的;(2)、的面积为______.(3)、在直线上确定点 , 使得最小. -
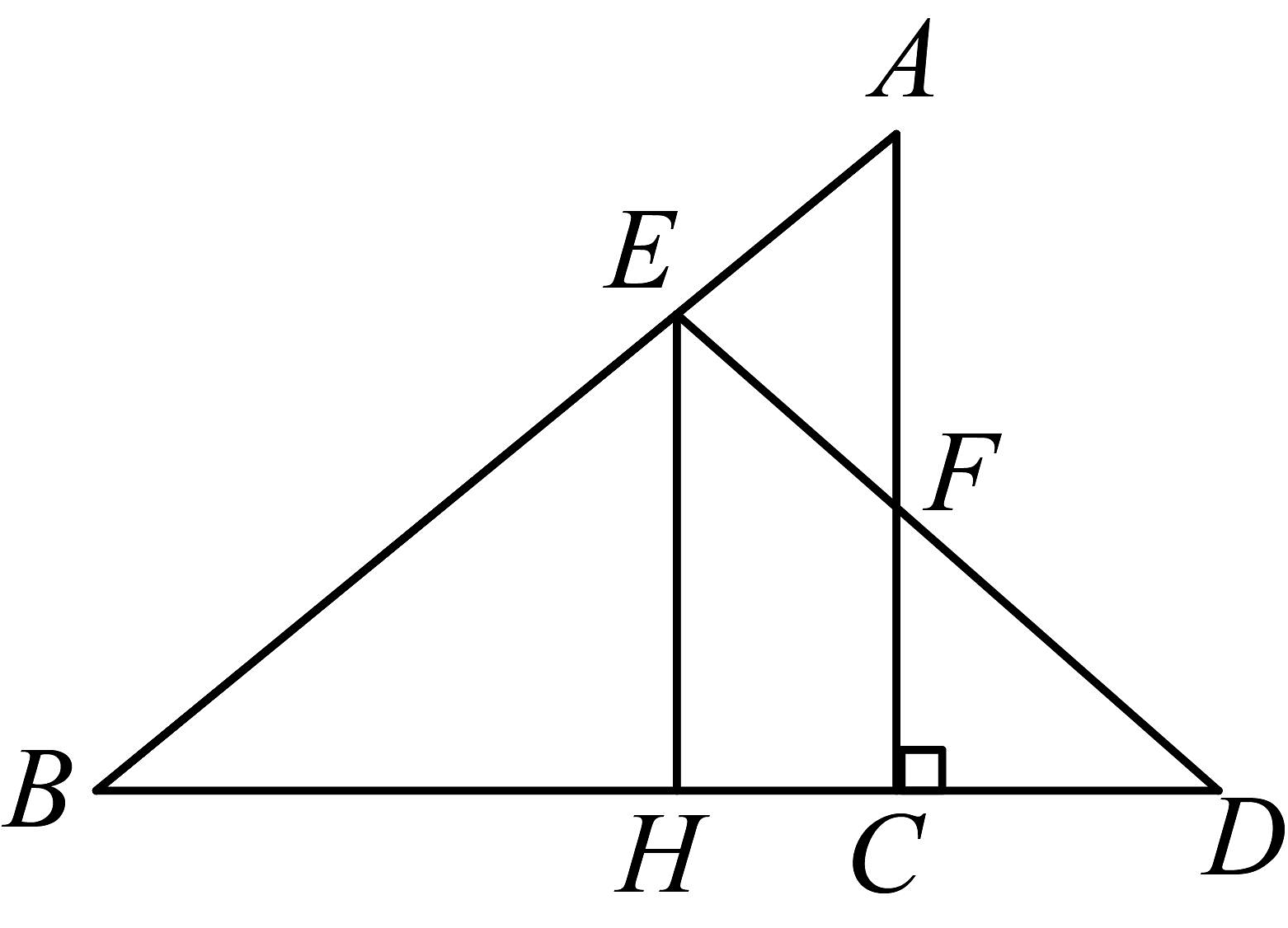
10、如图,已知D为边延长线上一点,于F交于E, , , 求的度数.

-
11、如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=6,则PD= .

-
12、如图,在 中, , , 的垂直平分线交 于点 , 的垂直平分线交 于点 , 则 度.

-
13、如图,要测量河两岸相对两点、间的距离,先在过点的的垂线上取两点、 , 使 , 再在过点的垂线上取点 , 使、、三点在一条直线上,可证明 , 所以测得的长就是、两点间的距离,这里判定的理由是 .

-
14、如图,在中,是角平分线,于点 , 的面积为15, , , 则的长是( )
 A、3 B、4 C、5 D、2
A、3 B、4 C、5 D、2 -
15、数学课上,同学们探讨利用不同画图工具画角的平分线的方法,小旭说:我用两块含的直角三角板就可以画角平分线,如图,取 , 把直角三角板按如图所示的位置放置,两直角边交于点 , 则射线是的平分线,小旭这样画的理论依据是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
16、如图,在中,、分别平分、 . 若 , 则( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
17、已知点 , 点与点关于轴对称,则点的坐标是( )A、 B、 C、 D、
-
18、已知一个三角形的两边长分别是8cm和5cm,则其第三边的长可以是( )A、1cm B、2cm C、3cm D、4cm
-
19、如图,已知点A,B,C从左到右依次在数轴上所表示的数分别为x, , 200,现将一把最小刻度为的刻度尺放到数轴上,测得点A与点B的距离为 .
 (1)、若数轴的1个单位长度为 .
(1)、若数轴的1个单位长度为 .①x的值为______;点A与点C的距离为______个单位长度;
②求点A,B,C所表示的数的和;.
(2)、若数轴的1个单位长度不是 , 且刻度尺上表示“8”和“10”的刻度分别对应数轴上的 , .①求x的值;
②若点D在数轴上,且点A与点C的距离是点A与点D的距离的2倍,求点D所表示的数;
③若刻度尺的最大刻度为 , 将数轴的单位长度变为原来后,用刻度尺能测量出数轴上点B与点C的距离,直接写出k的最小整数值.
-
20、已知: , , 根据下列条件求值:(1)、若 , 求的值;(2)、若 , 求的值;(3)、若 , 求的值.