相关试卷

1、计算 $\frac{y^{2}}{6 x} \cdot \frac{x^{2}}{y}$ 的结果是 ( )

A、 $\frac{y}{6 x}$ B、 $\frac{y}{6}$ C、xy D、 $\frac{x y}{6}$

查看解析
2、数学活动课上，老师准备了若干个如图①的三种纸片.甲种纸片是边长为a的正方形，乙种纸片是边长为b的正方形，丙种纸片是长为b、宽为a的长方形.

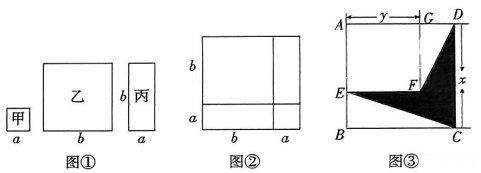(1)、【观察发现】用甲种纸片一张，乙种纸片一张，丙种纸片两张拼成如图②的大正方形.观察图②的面积关系，写出正确的等式：；

(2)、【操作探究】
若要拼出一个面积为（a+b）（a+2b）的长方形，则需要甲种纸片张，丙种纸片张，乙种纸片张；（所拼图形不重叠无缝隙）

(3)、【拓展延伸】两个正方形ABCD、AEFG如图③摆放，边长分别为x，y，连接CE，DF.若 $x^{2} + y^{2} = 52, D G = 2,$ 求图中阴影部分的面积.

查看解析
3、有些多项式不能直接运用提公因式法或公式法分解因式，但它可以通过适当的调整分组后，再利用提公因式法或公式法分组进行分解，这种对多项式先分组后分解因式的方法称为分组分解法，如 $a^{2} + 2 a b + b^{2} - 16$ $= {(a + b)}^{2} - 16 = (a + b + 4) (a + b - 4) .$ 请利用分组分解法解决下列问题：

(1)、分解因式： $4 x^{2} - 4 x y - 4 + y^{2} =$ .

(2)、已知a，b，c分别是 $△ A B C$ 的三边长，若 $a^{2} + c^{2} + a b - b c - 2 a c = 0,$ 试判断 $△ A B C$ 的形状，并说明理由.

查看解析
4、观察下列式子：
第1个等式： $3^{2} - 1^{2} = 8 \times 1,$
第2个等式： $5^{2} - 3^{2} = 8 \times 2,$
第3个等式： $7^{2} - 5^{2} = 8 \times 3,$
第4个等式： $9^{2} - 7^{2} = 8 \times 4,$
…
根据上述规律，解决下列问题：

(1)、写出第5个等式：；

(2)、写出你猜想的第n个等式（用含n的式子表示），并验证.

查看解析
5、如图①，是学校操场的示意图，操场跑道内部均铺满了草坪，将其抽象为如图②所示的几何图形，左右两边是半径为a米的半圆，中间是长为3.5a米的长方形.

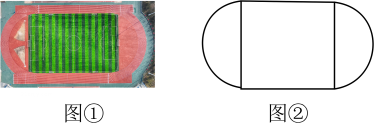(1)、利用因式分解表示草坪的面积；

(2)、当a=20时，求草坪的面积（π取3.14）.

查看解析

6、单单在因式分解

{(5 x + y)}^{2} -

{(x + 2 y)}^{2}

后，通过代入特殊值检验时，发现左右两边的值不相等，下面是她的解题过程，认真阅读并回答下列问题.

$(5 x + y)^{2} - (x + 2 y)^{2}$

=（5x+y+x+2y）（5x+y-x+2y） ①

=（6x+3y）（4x+3y） ②

=3（2x+y）（4x+3y） ③

单单的检验：

当 $x = 0, y = 1$ 时，

$(5 x + y)^{2} - (x + 2 y)^{2} = - 3;$

$| 3 (2 x + y) (4 x + 3 y) = 9,$

∵-3≠9，

∴分解因式错误.

(1)、单单的解题过程是从第步开始出错，出错的原因是；

(2)、请写出正确的因式分解过程.

查看解析

7、已知m为整数，试说明 ${(m + 8)}^{2} - {(m - 4)}^{2}$ 一定能被8整除.

查看解析
8、利用因式分解进行简便计算： $\frac{20 2^{2} - 404 \times 98 + 9 8^{2}}{20 2^{2} - 202 \times 98} .$

查看解析
9、分解因式：

(1)、 $x^{2} y - 2 x y + y;$

(2)、 $a^{2} (a - b) + (b - a) .$

查看解析
10、玉璧在中国传统玉文化中，一直是美好意愿和高贵品质的象征.如图①的玉璧是玉礼器中应用范围较为广泛的圆玉，从其正面看到的图形如图②所示，外圈半径为x+y，内圈半径为x-y，则该玉璧的面积为.

查看解析
11、若多项式 $A = 4 x^{2} - 3 x + 2, B = 3 x^{2} - x + 1,$ 则 A 与 B 的大小关系为

查看解析
12、如图是两个多项式因式分解的过程，根据你的发现，若 $x^{2} + 13 x + 36$ =（x+m）（x+n），则m+n的值为， mn的值为.

查看解析
13、如图，在边长为a的大正方形左上角挖去一个边长为b的小正方形（（b<a），将剩余图形拼成如图所示的长方形，通过计算阴影部分的面积，可以验证的等式是.

查看解析
14、多项式 $2 a x^{2} - 6 a x y$ 中，应提取的公因式是.

查看解析
15、已知a=2025x+2025，b=2025x+2026，c=2025x+2028，则 $a^{2} +$ $2 b^{2} + c^{2} - 2 a b - 2 b c$ 的值为（）

A、4 B、5 C、6 D、7

查看解析
16、已知a，b，c是一个三角形的三边长，则 ${(a - c)}^{2} - b^{2}$ 的值（）

A、一定为正数 B、一定为负数 C、一定为非负数 D、可能为零

查看解析
17、已知 $m^{2} + 3 m - 3 = 0,$ 则代数式 $m^{3} + 4 m^{2} + 13$ 的值为（）

A、14 B、16 C、18 D、20

查看解析
18、在数字化时代，密码是我们进入网络世界的第一道防线.辰辰通过查阅资料了解到有一种“因式分解”密码法，如将多项式 $x^{2} - 4$ 进行因式分解，若结果是（x+2）（x-2），代入“密钥”x=14，则得到两个因式的值分别是16，12，于是就得到一个密码“1612”.请完成第6~7题：

(1)、辰辰依据此原理给妈妈手机设置锁屏密码，他选取的多项式为 $4 x^{2} + 12 x + 9$ ，并选取他的幸运数字“9”作为“密钥”，则锁屏密码为（）

A、1212 B、2121 C、1122 D、2211

(2)、妈妈受到这种方式的启发，选取了一个多项式 $x^{2} - 2 x - 3,$ 得到的对应密码为1317，请尝试分析对应的“密钥”为（）

A、14 B、15 C、16 D、17

查看解析
19、下列各式中，因式分解正确的是（）

A、 $a^{2} + b^{2} = (a + b) (a - b)$ B、 $x^{2} - 4 x y + 9 y^{2} = {(x - 3 y)}^{2}$ C、 $x^{2} + 3 x + 1 = x (x + 3) + 1$ D、 $2 x^{2} - 8 y^{2} = 2 (x + 2 y) (x - 2 y)$

查看解析
20、下列各式中，能用公式法进行因式分解的是（）

A、 $- a^{2} + b^{2}$ B、 $4 x^{2} - (- 9 y^{2})$ C、 $y x^{2} - x y^{2}$ D、 $m^{3} + 2 m^{2} n - m n^{2}$

查看解析

上一页 657 658 659 660 661 下一页跳转