版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、命题“至少有一个实数 $x$ ，使得 $x^{3} + 1 = 0$ ”的否定是（）

A、 $\exists x \in R$ ， $x^{3} + 1 = 0$ B、 $\forall x \in R$ ， $x^{3} + 1 = 0$ C、 $\exists x \in R$ ， $x^{3} + 1 \neq 0$ D、 $\forall x \in R$ ， $x^{3} + 1 \neq 0$

查看解析
2、如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为正方形， $P A ⊥$ 平面 $A B C D$ ， $P A = A B = 2$ ．

(1)、求证： $A D / /$ 平面 $P B C$ ；

(2)、求直线 $B D$ 平面 $P C D$ 夹角的正弦值；

(3)、求点 $B$ 到平面 $P C D$ 的距离．

查看解析
3、在正四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A A_{1} = 2 A B = 4$ ，点 $E$ 在线段 $C C_{1}$ 上，且 $\vec{C C_{1}} = 4 \vec{C E}$ ，点 $F$ 为BD中点，则点 $D_{1}$ 到直线EF的距离（）

A、 $\frac{\sqrt{114}}{3}$ B、 $\frac{\sqrt{114}}{2}$ C、 $\frac{\sqrt{74}}{2}$ D、 $\frac{\sqrt{74}}{3}$

查看解析
4、直线 $x + y + 1 = 0$ 分别与 $x$ 轴， $y$ 轴交于A，B两点，点 $P$ 在圆 ${(x - 2)}^{2} + y^{2} = 2$ 上，则 $△ A B P$ 面积的取值范围是（）

A、 $[\frac{1}{2}, \frac{5}{2}]$ B、 $[1, 5]$ C、 $[\frac{\sqrt{2}}{2}, \frac{3 \sqrt{2}}{2}]$ D、 $[\sqrt{2}, \frac{3 \sqrt{2}}{2}]$

查看解析
5、若双曲线 $C : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0, b > 0)$ 满足 $a = 2 b$ ，则 $C$ 的离心率为（）

A、 $\frac{3}{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{5}{4}$

查看解析
6、已知直线 $a x + 2 y - 2 = 0$ 与直线 $2 x + a y + 3 = 0$ 平行，则 $a =$ （）

A、±2 B、2 C、-2 D、 $\pm \sqrt{2}$

查看解析
7、已知集合 $A = {0, 2, 4}, B = {x | | x - 1 ∣ < 2}$ ，则 $A \cap B =$ （）

A、 ${0, 2}$ B、 ${0, 4}$ C、 ${2, 4}$ D、 ${0}$

查看解析
8、已知函数 $f (x)$ 是定义在 $R$ 上的奇函数，且当 $x \leq 0$ 时， $f (x) = x^{2} + 4 x$ ，函数 $f (x)$ 在 $y$ 轴左侧的图象如图所示，请根据图象；

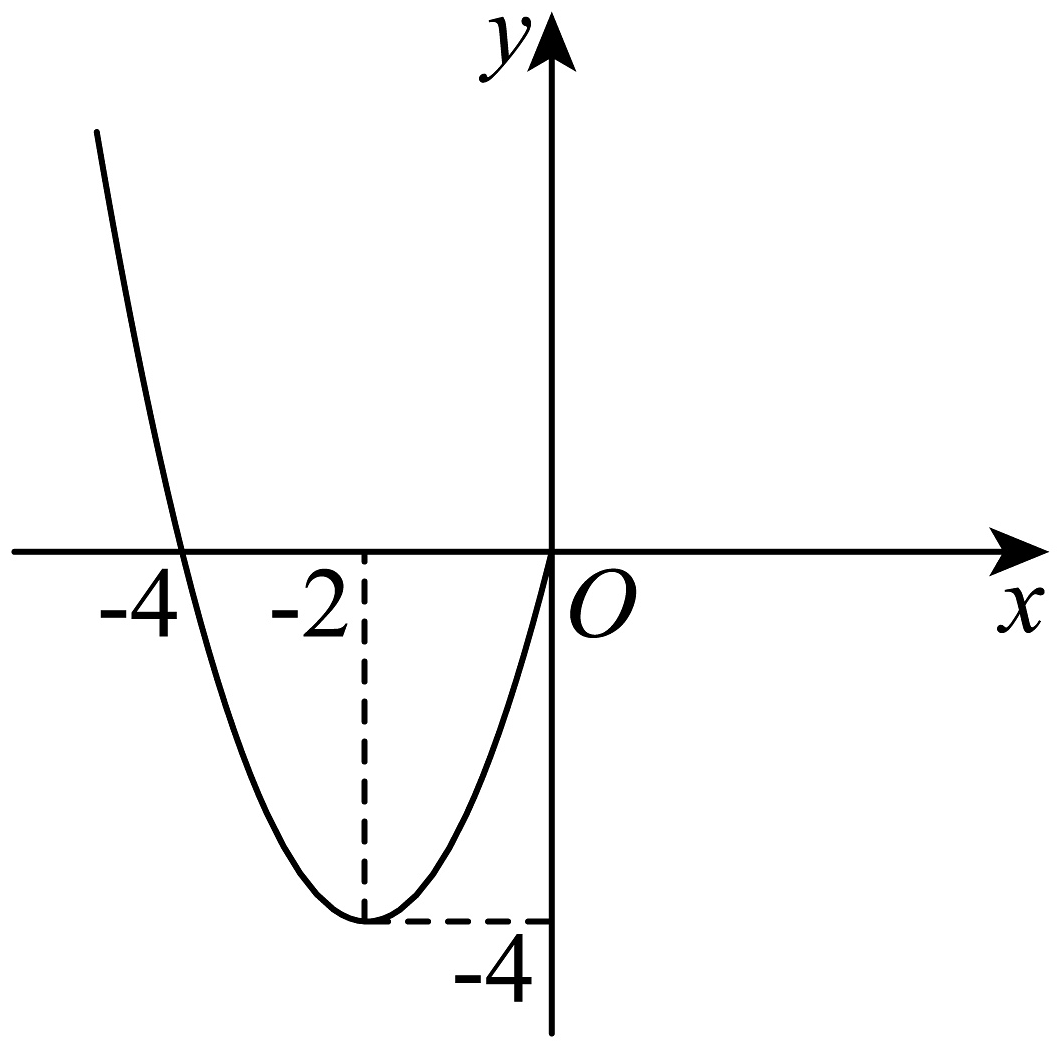(1)、画出 $f (x)$ 在 $y$ 轴右侧的图象，并写出函数 $f (x) (x \in R)$ 的单调区间；

(2)、写出函数 $f (x) (x \in R)$ 的解析式；

(3)、若函数 $g (x) = f (x) + (3 - a) x + 4 (x \in [2, 4])$ ，求函数 $g (x)$ 的最小值.

查看解析
9、已知函数 $f (x) = \frac{x}{x^{2} - 1}$ ，且其定义域为 $(- 1, 1)$ ．

(1)、判定函数 $f (x)$ 的奇偶性；

(2)、利用单调性的定义证明： $f (x)$ 在 $(0, 1)$ 上单调递减；

(3)、解不等式 $f (1 - m) + f (1 - m^{2}) < 0$ ．

查看解析
10、已知函数 $f (x + 1) = 2 x^{2} + 4 x + 3$

(1)、求函数 $f (x)$ 的解析式；

(2)、求关于 $x$ 的不等式 $f (x) - 2 a x > a + 1 - x$ 解集.（其中 $a \in R$ ）

查看解析
11、已知集合 $A = {x | - 3 < x \leq 4}$ ，集合 $B = \{x | k + 1 \leq x \leq 2 k - 1\}$ .

(1)、当 $k = 2$ 时，求 $A \cup B, (∁_{R} A) \cap B$ ；

(2)、若 $A \cup B = A$ ，求 $k$ 的取值范围．

查看解析
12、（1）已知 ${log}_{(x - 2)} (x^{2} - 7 x + 13) = 0$ ，求 $x$ 的值；
（2）已知 $a^{\frac{1}{2}} + a^{- \frac{1}{2}} = 3$ （ $a > 0$ ），求值： $\frac{a^{2} + a^{- 2} + 1}{a + a^{- 1} + 1}$ .

查看解析
13、某商店进货单价为45元，若按50元一个销售，能卖出50个，若销售单价每涨1元，其销售量就减少2个，为了获得最大利润，此商品的最佳售价应为每个元.

查看解析
14、已知函数 $f (x) = \{\begin{matrix} 4 x - 2 ， x < 1 \\ 3^{x} ， x \geq 1 \end{matrix}$ 则 $f (f (\frac{3}{4})) =$ .

查看解析
15、若 $\log_{5} (\log_{3} (\log_{2} x)) = 0 ， x =$ ．

查看解析
16、下列运算正确的是（）

A、 $2 \log_{\frac{1}{5}} 10 + \log_{\frac{1}{5}} 0.25 = 2$ B、 $\log_{4} 27 \cdot \log_{25} 8 \cdot \log_{9} 5 = \frac{9}{8}$ C、 $\lg 2 + \lg 50 = 2$ D、 $9^{\frac{1}{2}} + \ln e = 4$

查看解析
17、已知集合 $P = \{x | (x - 3) (x - 2) = 0\}$ ，则下列关系式表示正确的有（）

A、 $\{3\} \in P$ B、 $- 2 \in P$ C、 $\emptyset \subseteq P$ D、 $P \subseteq \{2, 3\}$

查看解析
18、已知函数 $f (x) = \{\begin{cases} a x^{2} - 2 x - a, x \geq 1 \\ (a + 3) x - 1, x < 1 \end{cases}$ ，在 $R$ 上单调递减，则实数a的取值范围是（）

A、 $(- \infty, - 3)$ B、 $[- 4, - 3)$ C、 $[- 4, 0)$ D、 $(- 4, 0)$

查看解析
19、已知幂函数 $f (x) = (b - 1) x^{a}$ 的图象过点 $(\sqrt{3}, \frac{1}{3})$ ，则 $a + b$ 等于（）

A、 $\frac{3}{2}$ B、0 C、 $\frac{1}{2}$ D、1

查看解析
20、若 $0 < t < 1$ ，则不等式 $(x - t) (x - \frac{1}{t}) < 0$ 的解集是（）

A、 $(\frac{1}{t}, t)$ B、 $(- \infty, t) \cup (\frac{1}{t}, + \infty)$ C、 $(- \infty, - \frac{1}{t}) \cup (- t, + \infty)$ D、 $(t, \frac{1}{t})$

查看解析

上一页 885 886 887 888 889 下一页跳转