相关试卷
-
1、已知直线与 , 若 , 则 , 之间的距离是( )A、 B、 C、 D、
-
2、在四棱锥中,底面 , 且 , 四边形是直角梯形,且 , , , , 为中点,在线段上,且 .
 (1)、求证:平面;(2)、求直线与平面所成角的正弦值.(3)、求点到平面的距离.
(1)、求证:平面;(2)、求直线与平面所成角的正弦值.(3)、求点到平面的距离. -
3、年月日,成都市举办马拉松比赛,其中志愿者的服务工作是马拉松成功举办的重要保障.当时成都市文体广电旅游局承办了志愿者选拔的面试工作.随机抽取了名候选者的面试成绩,并分成五组:第一组 , 第二组 , 第三组 , 第四组 , 第五组 , 绘制成如图所示的频率分布直方图.
 (1)、求的值,并估计这名候选者面试成绩的平均数;(2)、若从以上各组中用分层随机抽样的方法选取人,担任了本市的宣传者.若本市宣传者中第二组面试者的面试成绩的平均数和方差分别为和 , 第四组面试者的面试成绩的平均数和方差分别为和 , 请据此估计这次第二组和第四组所有面试者的面试成绩的方差.
(1)、求的值,并估计这名候选者面试成绩的平均数;(2)、若从以上各组中用分层随机抽样的方法选取人,担任了本市的宣传者.若本市宣传者中第二组面试者的面试成绩的平均数和方差分别为和 , 第四组面试者的面试成绩的平均数和方差分别为和 , 请据此估计这次第二组和第四组所有面试者的面试成绩的方差.(附:设两组数据的样本量、样本平均数和样本方差分别为: , , ; , , , 记两组数据总体的样本平均数为.则总体样本方差.
-
4、的三个顶点分别是 , , .(1)、求边上的中线所在直线的方程;(2)、求的外接圆(为圆心)的标准方程.
-
5、同时掷两个骰子一次,计算向上的点数,求:(1)、点数之和是7的概率;(2)、点数中恰有一个奇数和一个偶数的概率.
-
6、空间直角坐标系中,过点且一个法向量为的平面的方程为 , 过点且方向向量为的直线的方程为 , 阅读上面材料,并解决下面问题:已知平面的方程为 , 直线是两个平面与的交线,则平面的法向量为;直线与平面所成角的正弦值为.
-
7、已知空间向量 , , 则向量在向量上的投影向量的坐标是
-
8、若向量且与的夹角余弦为 , 则等于( )A、2 B、 C、或 D、
-
9、从2名男生和2名女生中任意选出两人参加冬奥知识竞赛,则选出的两人恰好是一名男生和一名女生的概率是( )A、 B、 C、 D、
-
10、某校在运动会期间组织了20名啦啦队队员,她们的身高(单位:cm)数据按从小到大排序如下:
162 162 163 165 165 165 165 167 167 167
168 168 170 170 171 173 175 175 178 178
则这20名队员身高的第75百分位数为( )
A、171 B、172 C、173 D、174 -
11、为了了解高一、高二、高三学生的身体状况,现用比例分配分层随机抽样的方法抽出一个容量为1500的样本,三个年级学生数之比依次为 , 已知高一年级共抽取了300人,则高三年级抽取的人数为( )A、750 B、300 C、450 D、150
-
12、对于函数 , 若其定义域内存在实数满足 , 则称为“伪奇函数”.
(1)已知函数 , 试问是否为“伪奇函数”?说明理由;
(2)若幂函数使得为定义在上的“伪奇函数”,试求实数的取值范围;
(3)是否存在实数 , 使得是定义在上的“伪奇函数”,若存在,试求实数的取值范围;若不存在,请说明理由.
-
13、某手作特产店拟举行某产品的促销活动,经调查测算,该产品的年销售量万份与年促销投入费用万元满足(为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知店内生产该产品的固定投入(设备等)为8万元,每生产一万件该产品需要再投入4万元,店家将每件产品的销售价格定为每件产品年平均成本的1.5倍(每件产品年平均成本按元来计算),按需生产,生产出的产品恰好被全部售出.(1)、将该产品的年利润万元表示为年促销费用万元的函数;(2)、该店家的促销投入费用为多少万元时,利润最大?最大利润是多少?
-
14、化简:(1)、;(2)、;
-
15、若函数在定义域内的某区间上单调递增,且在上也单调递增,则称在上是“强增函数”,则下列说法正确的是( )A、若函数 , 则存在使是“强增函数” B、若函数 , 则为定义在上的“强增函数” C、若函数 , 则存在区间 , 使在上不是“强增函数” D、若函数在区间上是“强增函数”,则
-
16、若 , , , 其中表示 , , 中的最大者,表示 , , 中的最小者,下列说法不正确的是( )A、函数为偶函数 B、当时,有 C、不等式的解集为 D、当时,有
-
17、函数的单调递减区间是( )A、 B、 C、 D、
-
18、函数的部分图象大致为( )A、
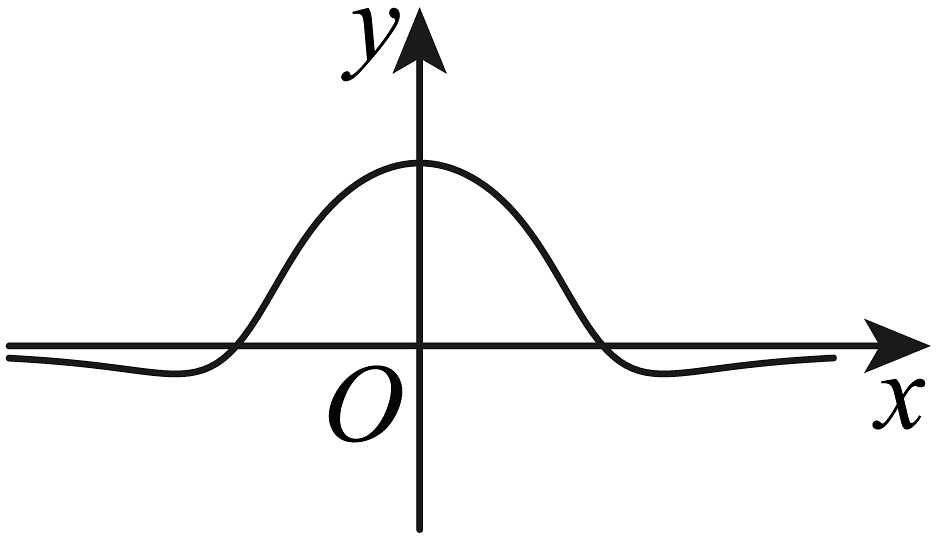 B、
B、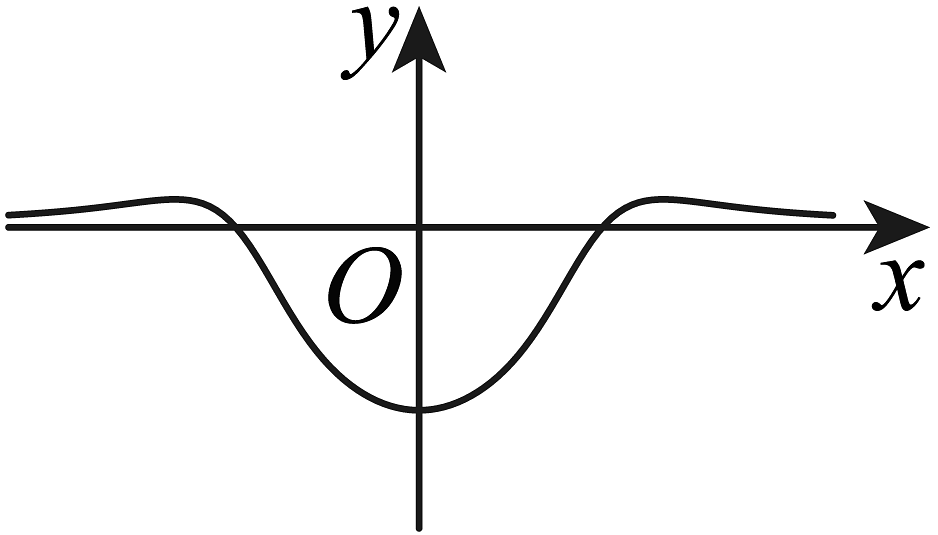 C、
C、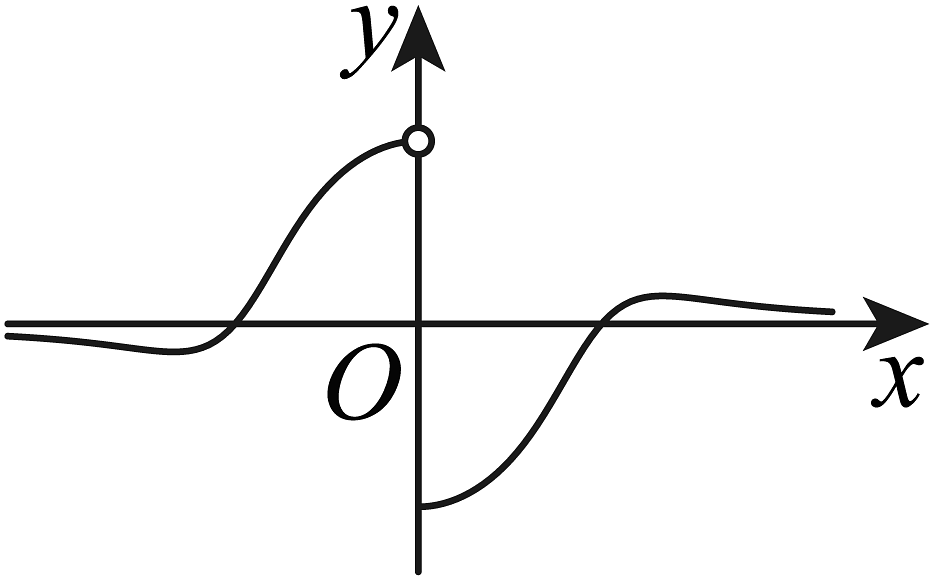 D、
D、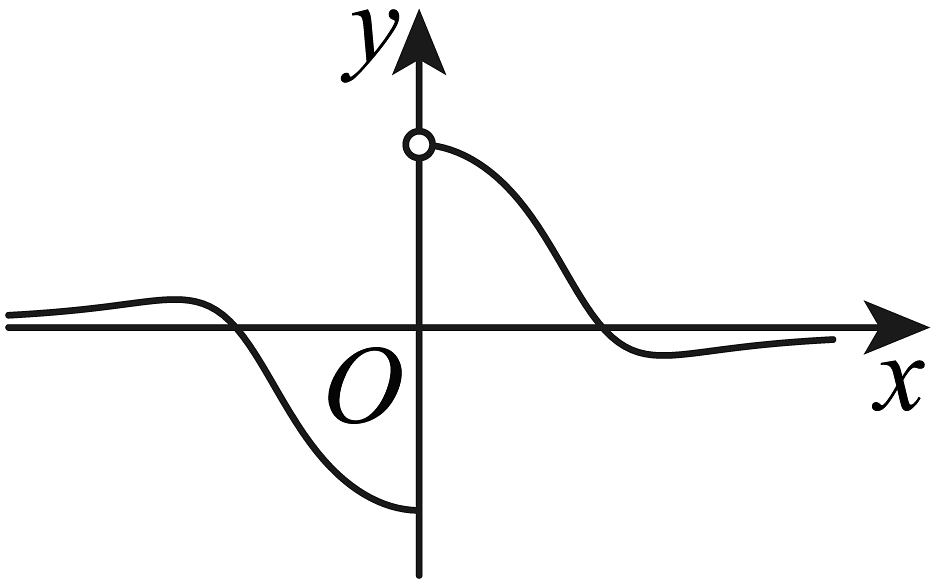
-
19、设 , 则“”是“”的( )A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件
-
20、若集合 , 则( )A、 B、 C、 D、