相关试卷
-
1、设 , 过定点A的动直线和过定点B的动直线交于点 , 则的取值范围是.
-
2、为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成两组,每组只,其中组小鼠给服甲离子溶液,组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记为事件:“乙离子残留在体内的百分比不高于5.5”,根据直方图得到的估计值为0.30.
(1)、求乙离子残留百分比直方图中的值;(2)、求甲离子残留百分比的第百分位数;(3)、估计乙离子残留百分比的均值.(同一组数据用该组区间的中点值为代表) -
3、若扇形的面积为、半径为1,则扇形的圆心角为( )A、 B、 C、 D、
-
4、已知函数 .(1)、若 , 求函数的单调区间和最值;(2)、若 , 且一次函数的图象和曲线相切于处,求函数的解析式并证明:恒成立.(3)、若 , 且函数在上有两个极值点,求实数的取值范围.
-
5、如图,在四棱锥中,底面是菱形, , 侧面是正三角形,是棱的中点.
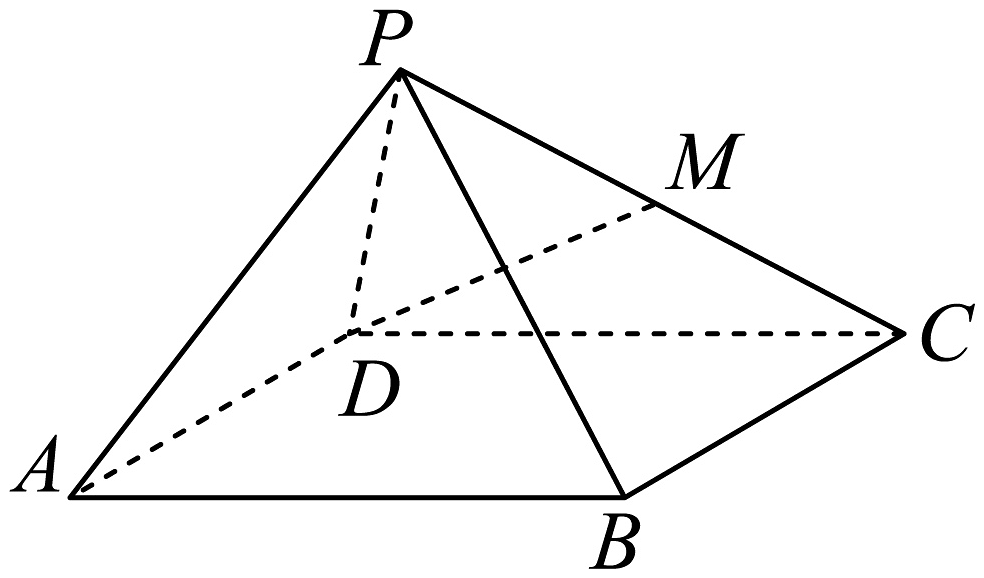 (1)、证明:;(2)、若二面角为 , 求直线与平面所成角的正弦值.
(1)、证明:;(2)、若二面角为 , 求直线与平面所成角的正弦值. -
6、已知双曲线与过点 , 的直线有且只有一个公共点 , 且双曲线的离心率 .(1)、求直线和双曲线的方程;(2)、设 , 为双曲线的左、右焦点,为线段的中点,求证: .
-
7、在中,角的对边分别为 , , , 已知 , .(1)、求角和角 .(2)、若边上的高为 , 求的面积.
-
8、已知曲线在处的切线恰好与曲线相切,则实数的值为 .
-
9、在正四棱柱中, , 点是棱上的动点(不含端点),则( )A、过点有且仅有一条直线与直线 , 都垂直 B、过点有且仅有一条直线与直线 , 都相交 C、有且仅有一个点满足和的面积相等 D、有且仅有一个点满足平面平面
-
10、随机变量 , 分别服从正态分布和二项分布,且 , , 则( )A、 B、 C、 D、
-
11、已知函数的定义域为 , 当或或是无理数时,;当( , , 是互质的正整数)时, . 那么当 , , , 都属于时,下列选项恒成立的是( )A、 B、 C、 D、
-
12、函数在区间上的所有零点之和为( )A、 B、 C、 D、4
-
13、已知底面半径为2的圆锥 , 其轴截面是正三角形,它的一个内接圆柱的底面半径为1,则此圆柱侧面积与圆锥侧面积的比值为( )A、1 B、 C、 D、
-
14、二项式的展开式中的常数项为( )A、480 B、240 C、120 D、15
-
15、若过点与圆相切的两条直线的夹角为 , 则( )A、 B、 C、 D、
-
16、已知 , 则( )A、 B、1 C、 D、2
-
17、已知集合 , 集合 , 则( )A、 B、 C、 D、
-
18、一般地,任何一个复数(a,)可以写成 , 其中r是复数的模,是以x轴非负半轴为始边,射线OZ为终边的角,称为复数的辅角.我们规定在范围内的辅角称为辅角主值,通常记作argz,如 , , .发现 , 就是说两个复数相乘,积的模等于各复数模的积,积的辅角等于各复数辅角的和.考虑如下操作:从写有实数0,1,的三张卡片中随机抽取两张,将卡片上的两个数依次作为一个复数的实部和虚部.设n为正整数,重复n次上述操作,可得到n个复数,将它们的乘积记为.(1)、写出一次操作后所有可能的复数;(2)、当 , 记的取值为X,求X的分布列;(3)、求为实数的概率.
-
19、在平面直角坐标系中,圆C的方程为: , 定点 , B是圆C上任意一点,线段BF的垂直平分线l和半径BC相交于点T.(1)、求点T的轨迹W的方程;(2)、已知点 , 过点F的一条直线,斜率不为0,交曲线W于P、Q两点,直线AP,AQ分别与直线交于M,N两点,求证:直线FM与直线FN的斜率之积为常数.
-
20、如图,三棱锥中, , 平面平面 , 平面平面.
 (1)、证明:平面;(2)、若为钝角,且二面角的大小为 , 求.
(1)、证明:平面;(2)、若为钝角,且二面角的大小为 , 求.