相关试卷
-
1、如图,在三棱柱中,D,E分别是线段 , 的中点,设 , , .用 , , 表示.
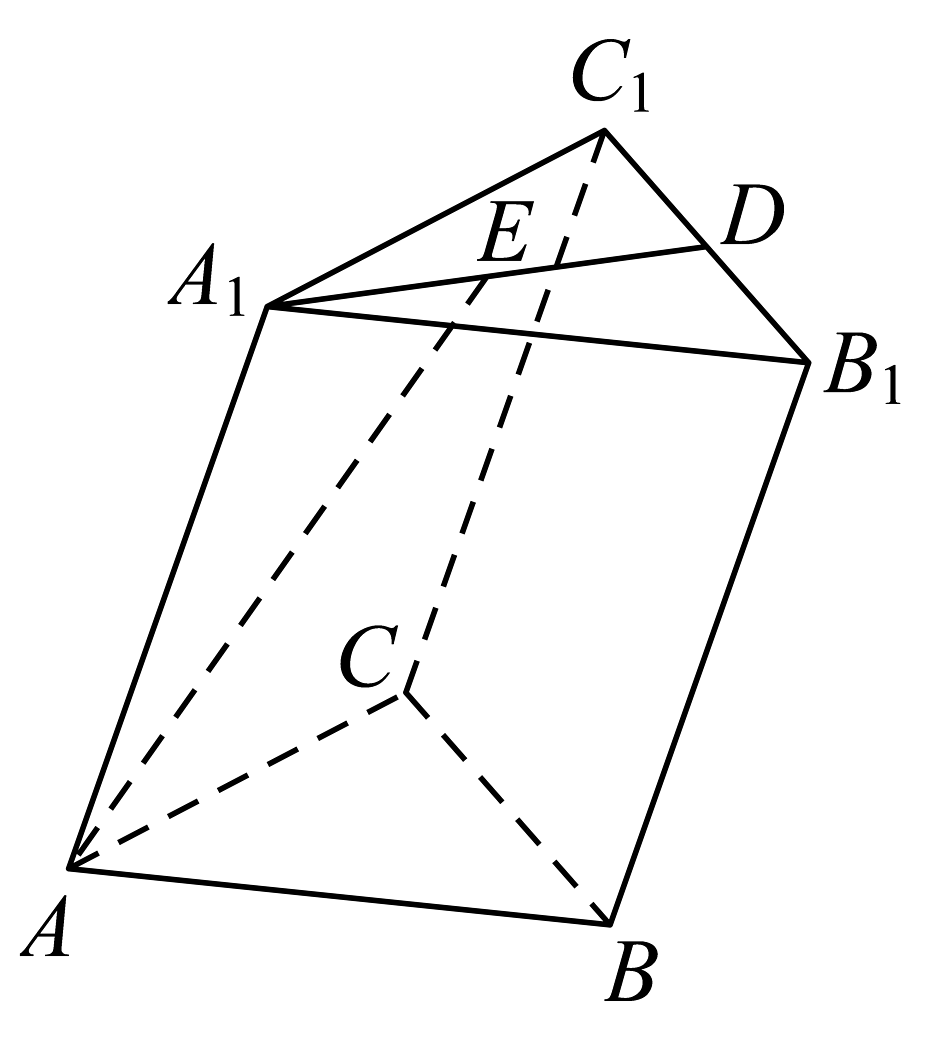
-
2、定义:由椭圆的一个焦点和长轴的一个顶点(焦点与顶点在同一边)和短轴的一个顶点组成的三角形称为该椭圆的“焦顶三角形”,如果两个椭圆的”焦顶三角形”相似,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比,下列问题中(对应图1,对应图2).
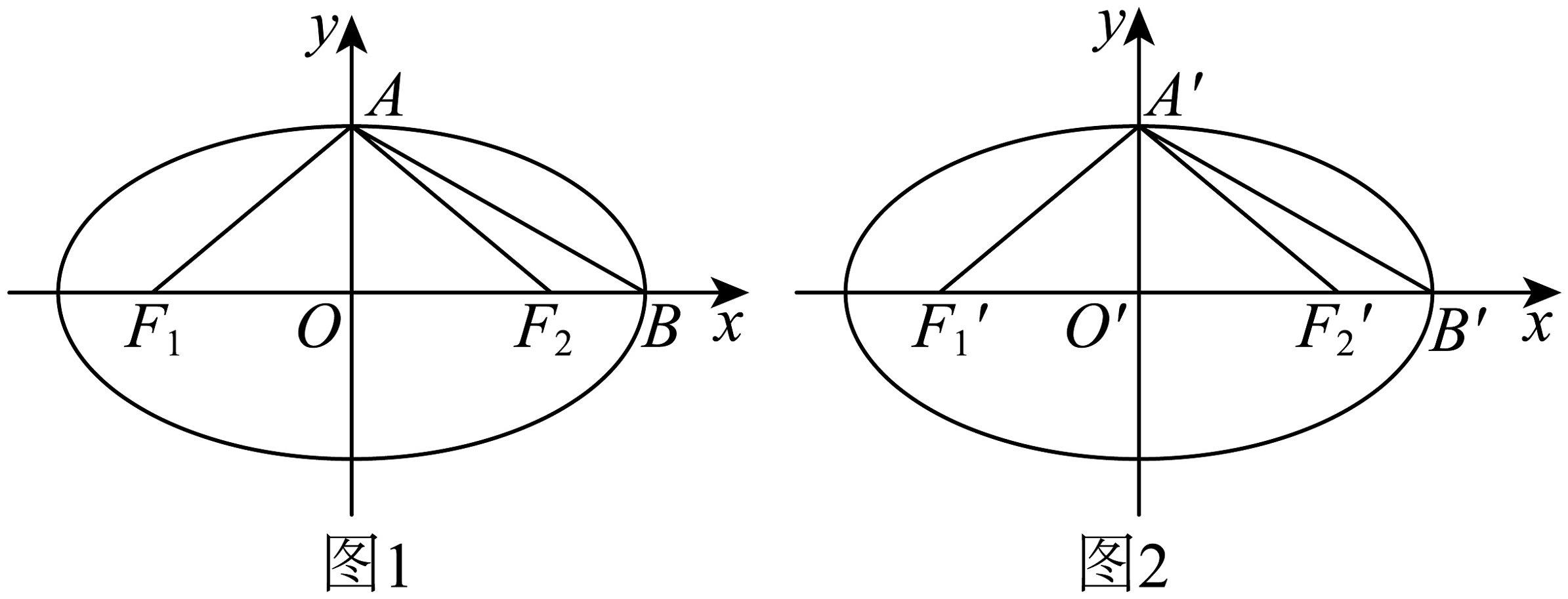 (1)、判断椭圆与椭圆是否是“相似椭圆”? 若是,求出相似比;若不是,请说明理由;(2)、证明:两个椭圆是“相似椭圆”的充要条件是离心率相等;(3)、已知椭圆椭圆的离心率为 , 与是“相似椭圆”,且与的相似比为 , 若的面积为 , 求的面积(用 , , 表示).
(1)、判断椭圆与椭圆是否是“相似椭圆”? 若是,求出相似比;若不是,请说明理由;(2)、证明:两个椭圆是“相似椭圆”的充要条件是离心率相等;(3)、已知椭圆椭圆的离心率为 , 与是“相似椭圆”,且与的相似比为 , 若的面积为 , 求的面积(用 , , 表示). -
3、已知向量 , 则下列结论正确的是( )A、向量与向量的夹角为 B、 C、向量在向量上的投影向量为 D、向量与向量共面
-
4、已知函数( , )的图象关于直线对称,且图象上相邻两个最高点的距离为.(1)、求和的值;(2)、当时,求函数的最大值和最小值;(3)、设 , 若图象的任意一条对称轴与轴的交点的横坐标不属于区间 , 求的取值范围.
-
5、如图所示,下列频率分布直方图显示了三种不同的分布形态.图(1)形成对称形态,图(2)形成“右拖尾”形态,图(3)形成“左拖尾”形态,根据所给图作出以下判断,正确的是( )
 A、图(1)的平均数=中位数=众数 B、图(2)的众数<中位数<平均数 C、图(2)的众数<平均数<中位数 D、图(3)的平均数<中位数<众数
A、图(1)的平均数=中位数=众数 B、图(2)的众数<中位数<平均数 C、图(2)的众数<平均数<中位数 D、图(3)的平均数<中位数<众数 -
6、下列事件中,是相互独立事件的是( )A、一枚硬币掷两次,“第一次为正面”,“第二次为反面” B、袋中有2个白球,2个黑球,不放回地摸两球,“第一次摸到白球”,“第二次摸到白球” C、掷一枚骰子,“出现点数为奇数”,“出现点数为3或4” D、掷一枚骰子,“出现点数为奇数”,“出现点数为偶数”
-
7、已知直线 , , 则( )A、当时,直线的一个方向向量为 B、若与相互平行,则或 C、若 , 则 D、若不经过第二象限,则
-
8、已知随机事件A,B,C中,与相互独立,与对立,且 , , 则( )A、0.4 B、0.58 C、0.7 D、0.72
-
9、设、 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
10、设 , 过定点A的动直线和过定点B的动直线交于点 , 则的取值范围是.
-
11、为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成两组,每组只,其中组小鼠给服甲离子溶液,组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记为事件:“乙离子残留在体内的百分比不高于5.5”,根据直方图得到的估计值为0.30.
(1)、求乙离子残留百分比直方图中的值;(2)、求甲离子残留百分比的第百分位数;(3)、估计乙离子残留百分比的均值.(同一组数据用该组区间的中点值为代表) -
12、若扇形的面积为、半径为1,则扇形的圆心角为( )A、 B、 C、 D、
-
13、已知函数 .(1)、若 , 求函数的单调区间和最值;(2)、若 , 且一次函数的图象和曲线相切于处,求函数的解析式并证明:恒成立.(3)、若 , 且函数在上有两个极值点,求实数的取值范围.
-
14、如图,在四棱锥中,底面是菱形, , 侧面是正三角形,是棱的中点.
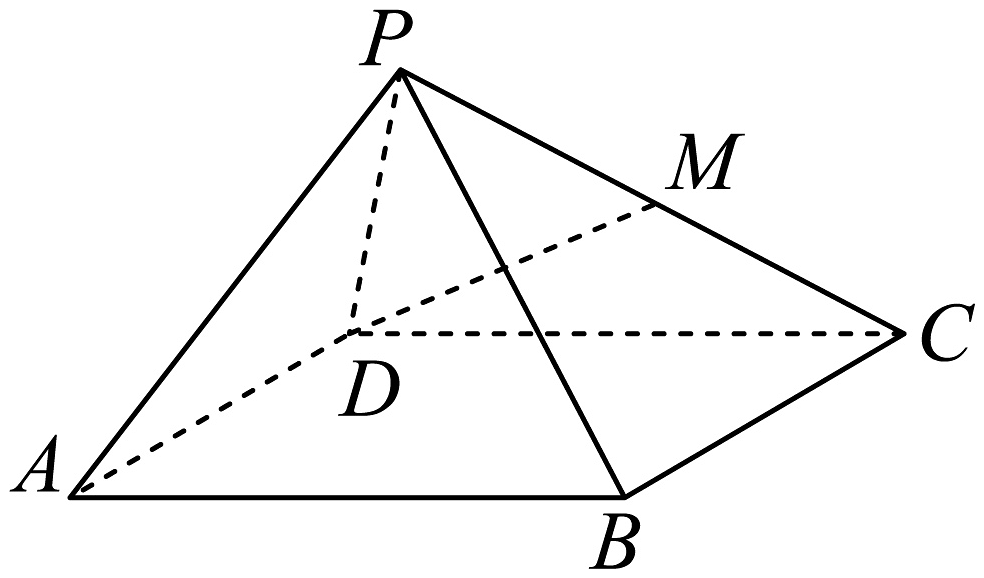 (1)、证明:;(2)、若二面角为 , 求直线与平面所成角的正弦值.
(1)、证明:;(2)、若二面角为 , 求直线与平面所成角的正弦值. -
15、已知双曲线与过点 , 的直线有且只有一个公共点 , 且双曲线的离心率 .(1)、求直线和双曲线的方程;(2)、设 , 为双曲线的左、右焦点,为线段的中点,求证: .
-
16、在中,角的对边分别为 , , , 已知 , .(1)、求角和角 .(2)、若边上的高为 , 求的面积.
-
17、已知曲线在处的切线恰好与曲线相切,则实数的值为 .
-
18、在正四棱柱中, , 点是棱上的动点(不含端点),则( )A、过点有且仅有一条直线与直线 , 都垂直 B、过点有且仅有一条直线与直线 , 都相交 C、有且仅有一个点满足和的面积相等 D、有且仅有一个点满足平面平面
-
19、随机变量 , 分别服从正态分布和二项分布,且 , , 则( )A、 B、 C、 D、
-
20、已知函数的定义域为 , 当或或是无理数时,;当( , , 是互质的正整数)时, . 那么当 , , , 都属于时,下列选项恒成立的是( )A、 B、 C、 D、