相关试卷
-
1、设点、 , 若直线与线段相交,则的取值范围是( )A、 B、 C、 D、
-
2、函数有两个零点的充分不必要条件是( )A、 B、 C、或 D、
-
3、已知 , 为第三象限角,则( )A、 B、 C、 D、
-
4、某同学掷骰子5次,记录了每次骰子出现的点数,则从以下情况中可以判断出这组数据一定没有出现点数6的是( )A、平均数为3,中位数为2 B、中位数为3,众数为2 C、中位数为3,方差为2.8 D、平均数为2,方差为2.4
-
5、已知复数 , 则( )A、 B、 C、 D、
-
6、在棱长为的正方体中,点分别为棱的中点. 点为正方体表面上的动点,满足. 给出下列四个结论:
①线段长度的最大值为;
②存在点 , 使得;
③存在点 , 使得;
④是等腰三角形.
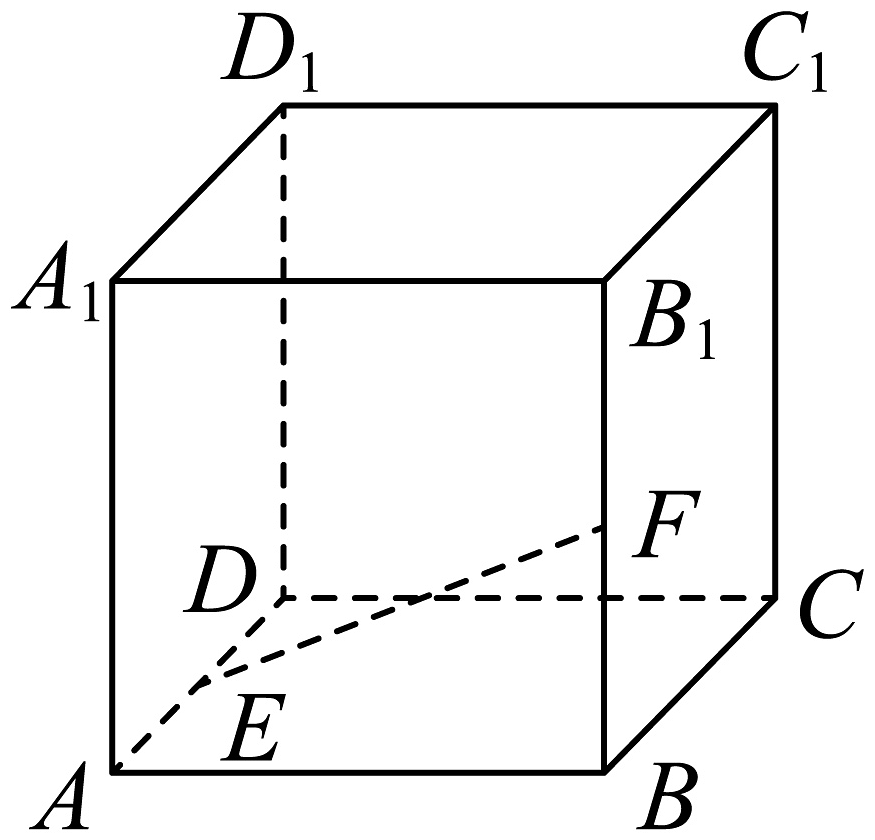
其中,所有正确结论的序号是 .
-
7、如图所示,已知点是的重心,过点作直线分别交两边于两点,且 , , 则的最小值为( )
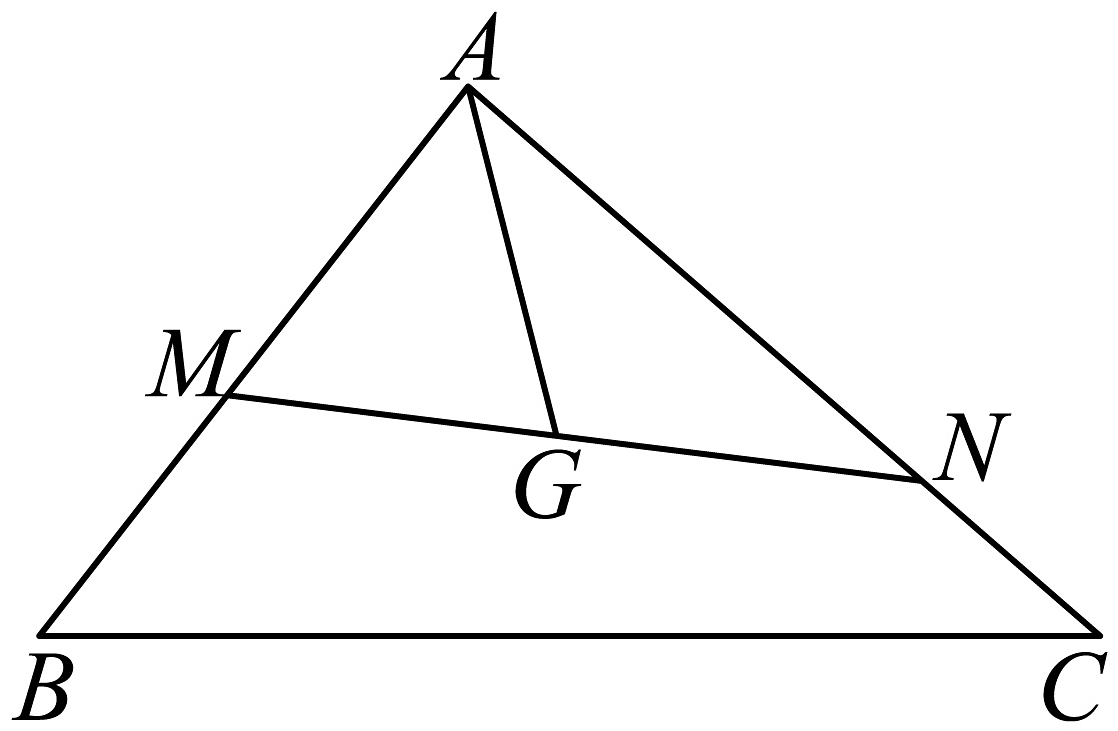 A、 B、 C、4 D、2
A、 B、 C、4 D、2 -
8、如图,在正六棱柱中,为的中点.设 , , .
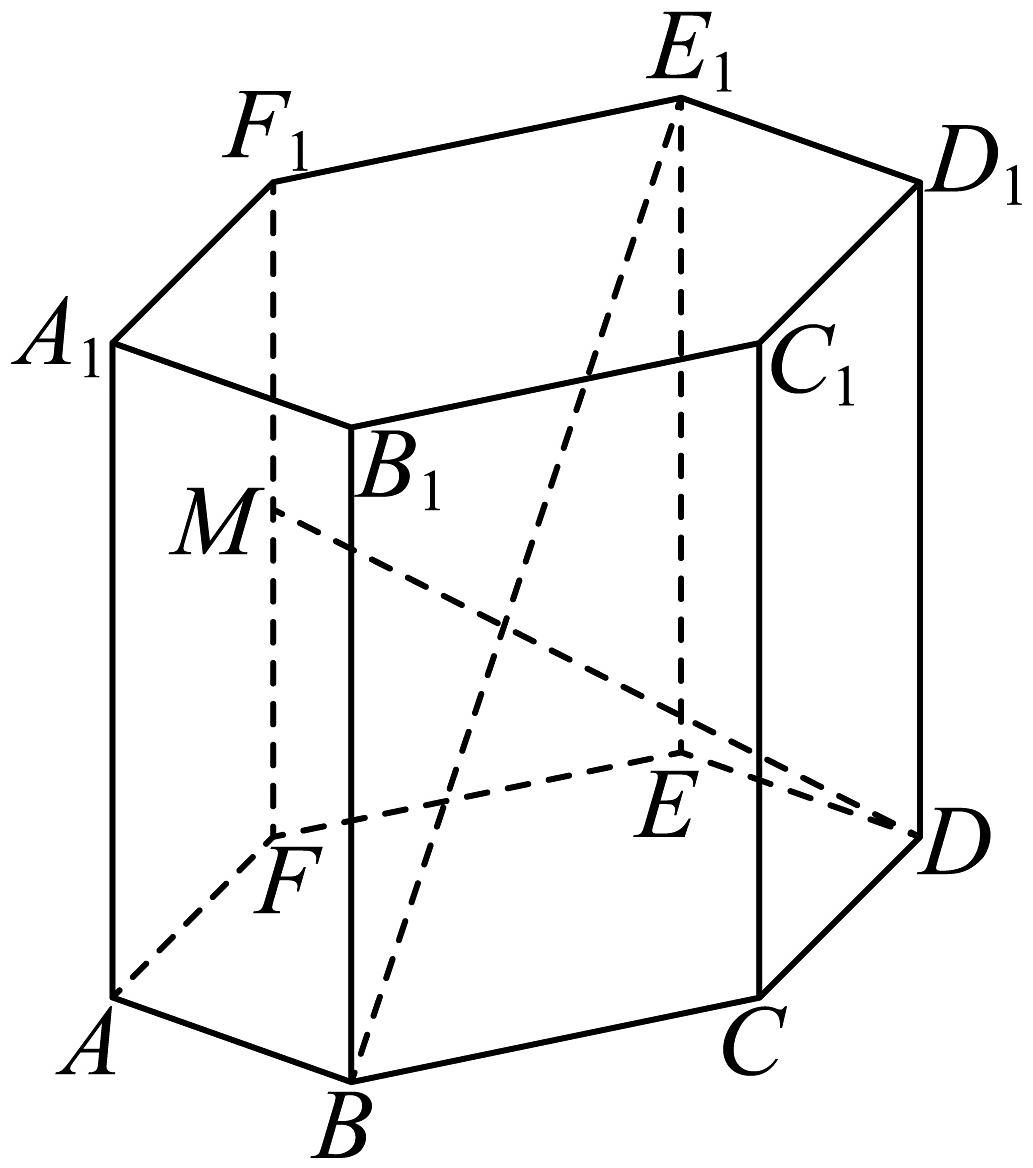 (1)、用 , , 表示向量 , ;(2)、若求的值.
(1)、用 , , 表示向量 , ;(2)、若求的值. -
9、已知 , 若直线与线段相交,则m的值可能为( )A、 B、4 C、10 D、
-
10、在我国古代数学名著《九章算术》中,四个面都为直角三角形的三棱锥称为鳖臑.已知在鳖臑中,平面ABC, . M为PC的中点,则点P到平面MAB的距离为 .

-
11、已知是两条不重合的直线, , , 是三个两两不重合的平面,给出下列四个命题:
①若则;
②若则;
③若则;
④若是异面直线,则 . 其中真命题是( )
A、①和② B、①和③ C、③和④ D、①和④ -
12、如图,在三棱柱中,D,E分别是线段 , 的中点,设 , , .用 , , 表示.
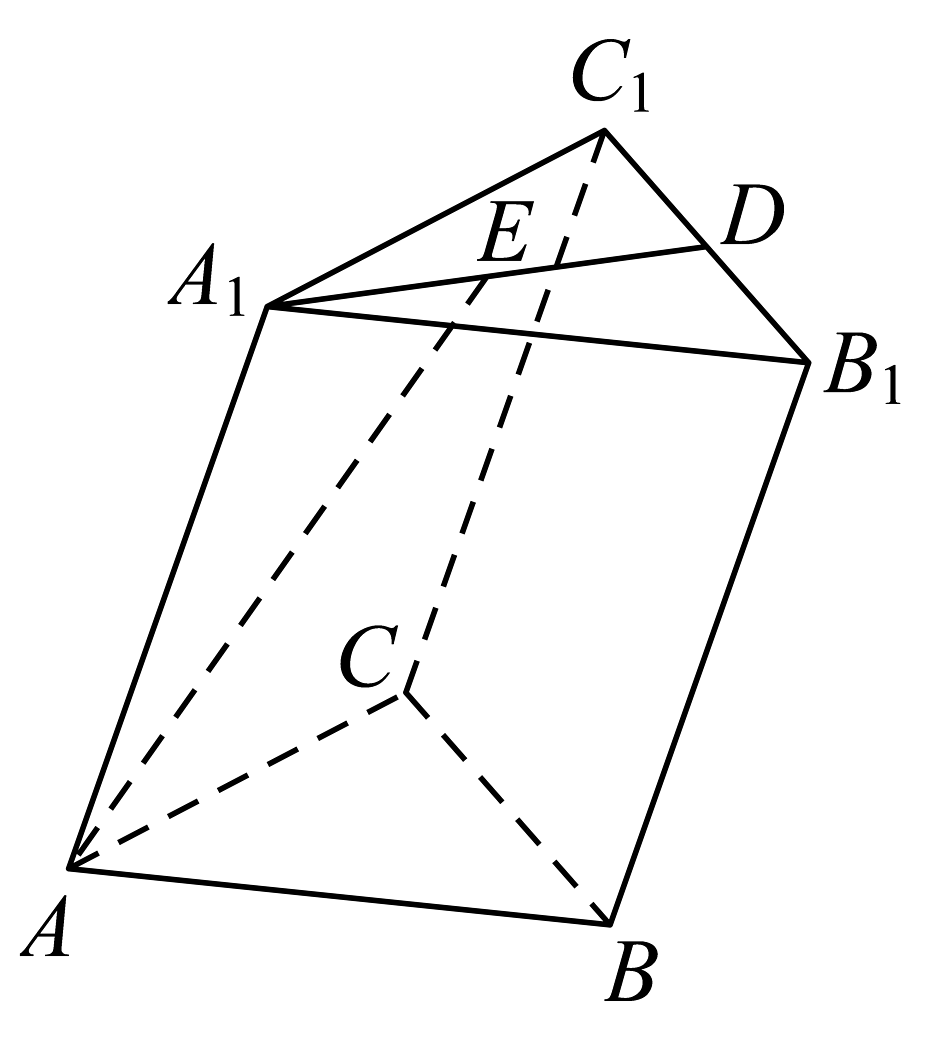
-
13、定义:由椭圆的一个焦点和长轴的一个顶点(焦点与顶点在同一边)和短轴的一个顶点组成的三角形称为该椭圆的“焦顶三角形”,如果两个椭圆的”焦顶三角形”相似,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比,下列问题中(对应图1,对应图2).
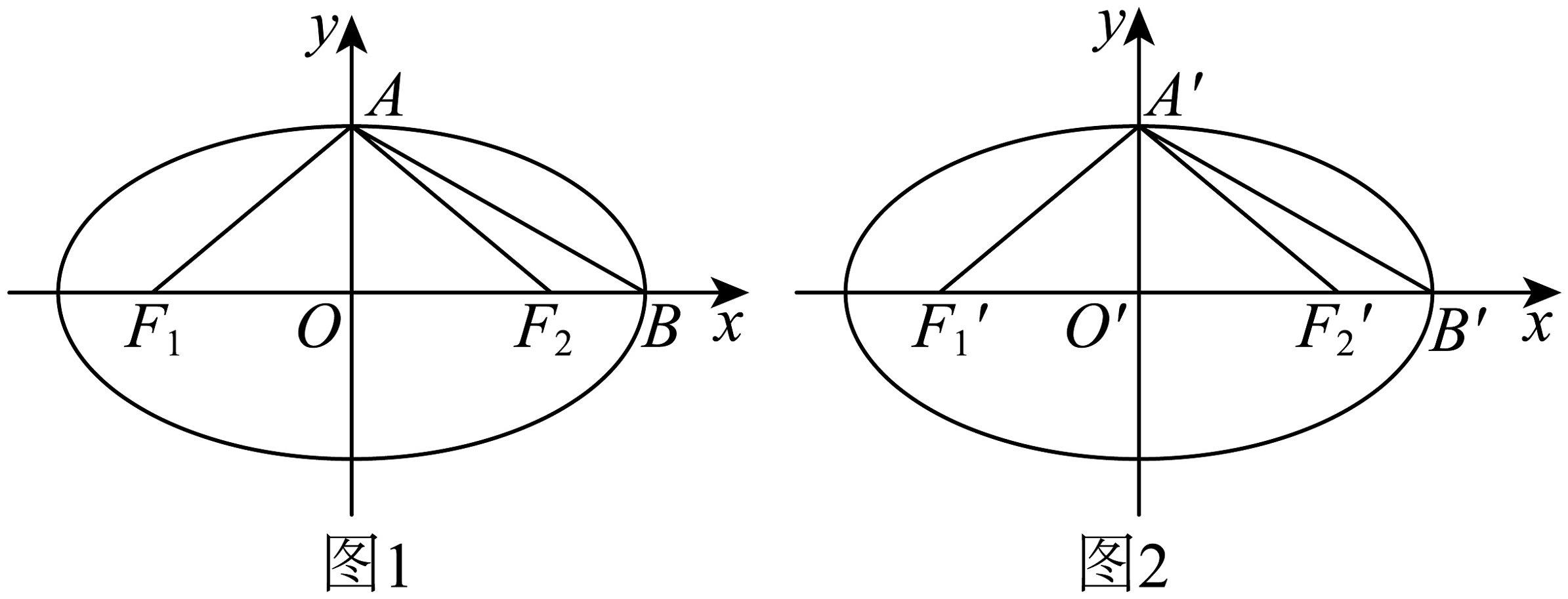 (1)、判断椭圆与椭圆是否是“相似椭圆”? 若是,求出相似比;若不是,请说明理由;(2)、证明:两个椭圆是“相似椭圆”的充要条件是离心率相等;(3)、已知椭圆椭圆的离心率为 , 与是“相似椭圆”,且与的相似比为 , 若的面积为 , 求的面积(用 , , 表示).
(1)、判断椭圆与椭圆是否是“相似椭圆”? 若是,求出相似比;若不是,请说明理由;(2)、证明:两个椭圆是“相似椭圆”的充要条件是离心率相等;(3)、已知椭圆椭圆的离心率为 , 与是“相似椭圆”,且与的相似比为 , 若的面积为 , 求的面积(用 , , 表示). -
14、已知向量 , 则下列结论正确的是( )A、向量与向量的夹角为 B、 C、向量在向量上的投影向量为 D、向量与向量共面
-
15、已知函数( , )的图象关于直线对称,且图象上相邻两个最高点的距离为.(1)、求和的值;(2)、当时,求函数的最大值和最小值;(3)、设 , 若图象的任意一条对称轴与轴的交点的横坐标不属于区间 , 求的取值范围.
-
16、如图所示,下列频率分布直方图显示了三种不同的分布形态.图(1)形成对称形态,图(2)形成“右拖尾”形态,图(3)形成“左拖尾”形态,根据所给图作出以下判断,正确的是( )
 A、图(1)的平均数=中位数=众数 B、图(2)的众数<中位数<平均数 C、图(2)的众数<平均数<中位数 D、图(3)的平均数<中位数<众数
A、图(1)的平均数=中位数=众数 B、图(2)的众数<中位数<平均数 C、图(2)的众数<平均数<中位数 D、图(3)的平均数<中位数<众数 -
17、下列事件中,是相互独立事件的是( )A、一枚硬币掷两次,“第一次为正面”,“第二次为反面” B、袋中有2个白球,2个黑球,不放回地摸两球,“第一次摸到白球”,“第二次摸到白球” C、掷一枚骰子,“出现点数为奇数”,“出现点数为3或4” D、掷一枚骰子,“出现点数为奇数”,“出现点数为偶数”
-
18、已知直线 , , 则( )A、当时,直线的一个方向向量为 B、若与相互平行,则或 C、若 , 则 D、若不经过第二象限,则
-
19、已知随机事件A,B,C中,与相互独立,与对立,且 , , 则( )A、0.4 B、0.58 C、0.7 D、0.72
-
20、设、 , 则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件