相关试卷
-
1、已知函数 .(1)、若直线与曲线相切,求的值;(2)、讨论的单调性;(3)、若在定义域内恒成立,求的取值范围.
-
2、如图,已知四棱锥的底面为菱形,.
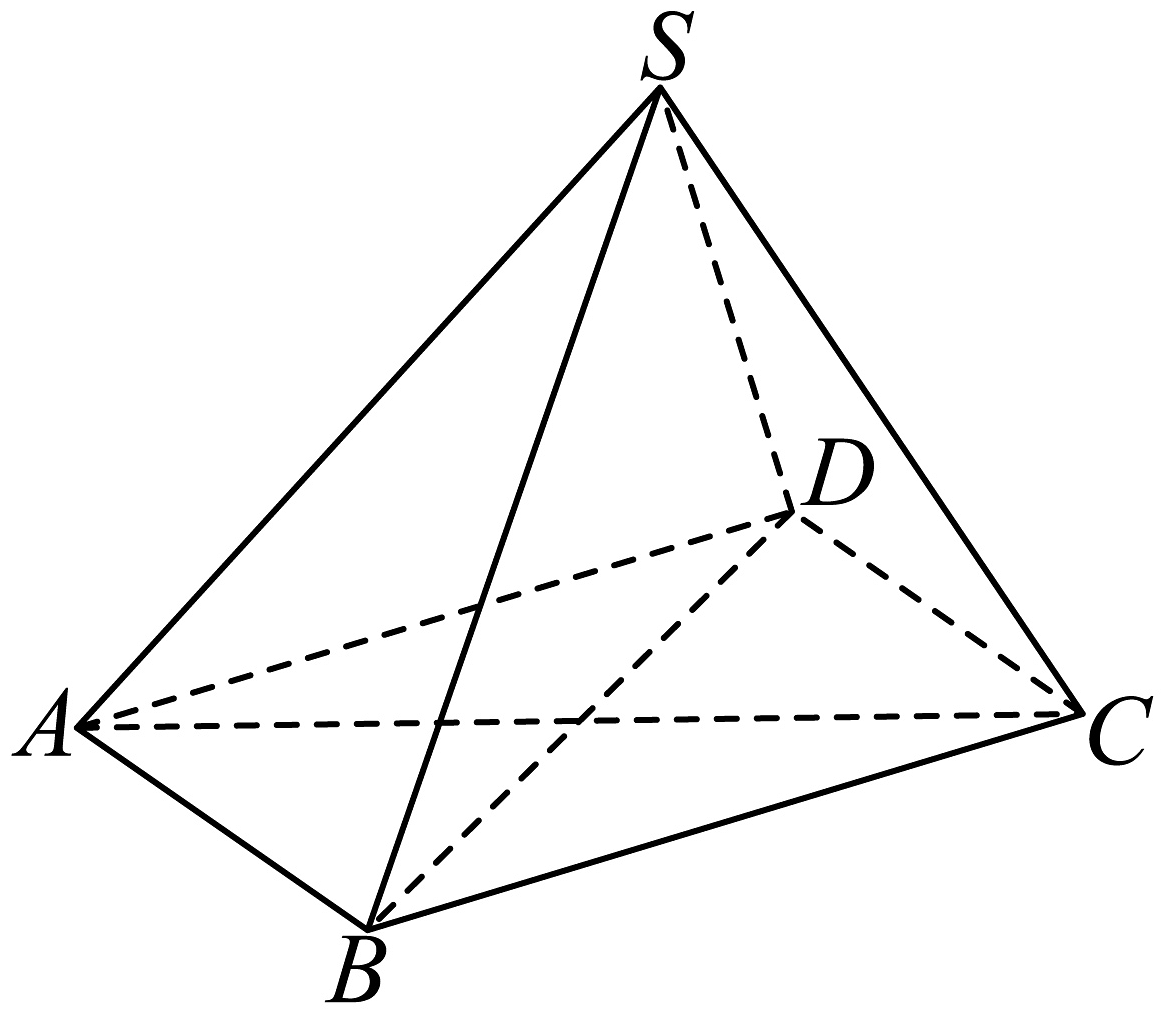 (1)、求证:平面BDS;(2)、若 , 求四棱锥的体积.
(1)、求证:平面BDS;(2)、若 , 求四棱锥的体积. -
3、记的内角A,B,C的对边分别为a,b,c.已知.(1)、求;(2)、若 , , 求.
-
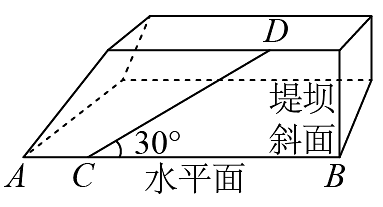
4、德阳市去年完工的华强沟水库是坝斜面与水平面所成的二面角为 , 堤坝斜面上有一条直道与堤脚的水平线的夹角为 , 小李同学沿这条直道从处向上行走到10米时,小李升高了米.
-
5、已知抛物线焦点为 , 抛物线上一点的横坐标为2,则 .
-
6、若函数在上不单调,则实数a的取值范围为.
-
7、若 , 则下列结论正确的是( )A、 B、数据的标准差为3 C、数据的分位数为10 D、记 , 随机变量 , , 则
-
8、在中,内角A,B,C的对边分别为a,b,c,下列说法正确的是( )A、若 , 则 B、 C、若 , 则是锐角三角形 D、若 , 则是钝角三角形
-
9、过双曲线的中心作直线与双曲线交于、两点,设双曲线的右焦点为 , 已知 , 则的面积为( )A、 B、1 C、 D、
-
10、已知为等差数列的前项和,若 , 则( )A、 B、 C、0 D、12
-
11、5件产品中有2件次品,现逐一检查,直至能确定所有次品为止,则第四次检测结束的概率为 ( )A、 B、 C、 D、
-
12、已知 , 则( )A、 B、 C、 D、
-
13、已知向量 , 若 , 则的值为( )A、4 B、5 C、 D、
-
14、已知集合 , , 则( )A、 B、 C、 D、
-
15、在中,角A,B,C的对边分别为a,b,c,若 , 则的面积( )A、1 B、 C、 D、
-
16、如图,四棱锥中,底面 , , , .
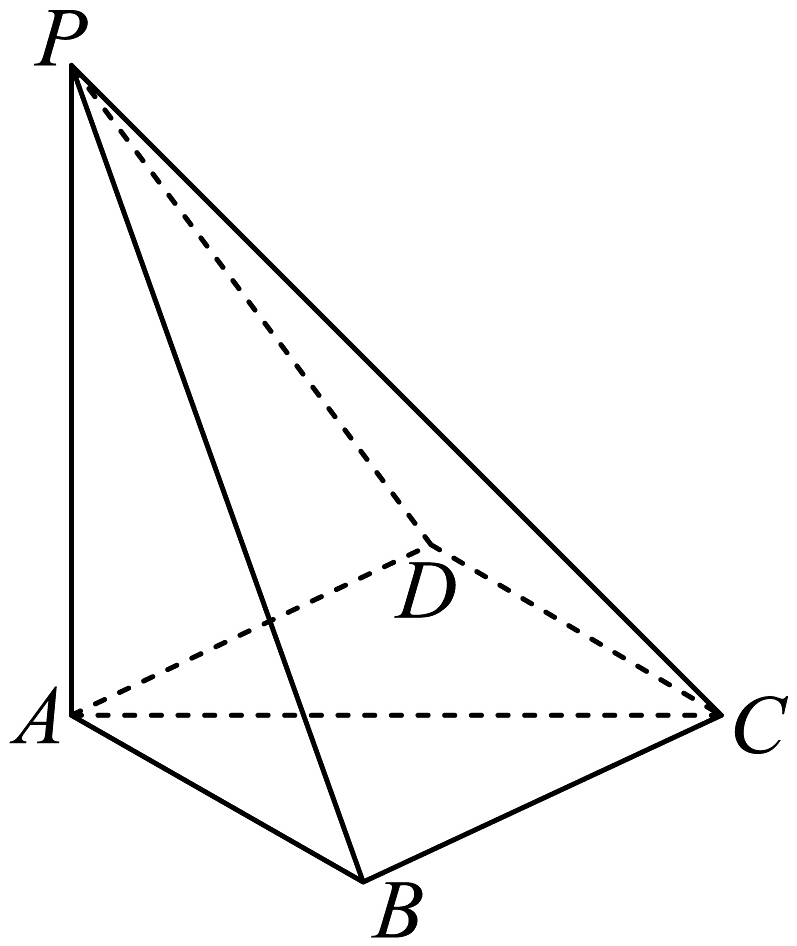 (1)、若G点为的重心,求;(2)、若 , 证明:平面;(3)、若 , 且二面角的正弦值为 , 求.
(1)、若G点为的重心,求;(2)、若 , 证明:平面;(3)、若 , 且二面角的正弦值为 , 求. -
17、在四棱锥中,面面 , , , , , .
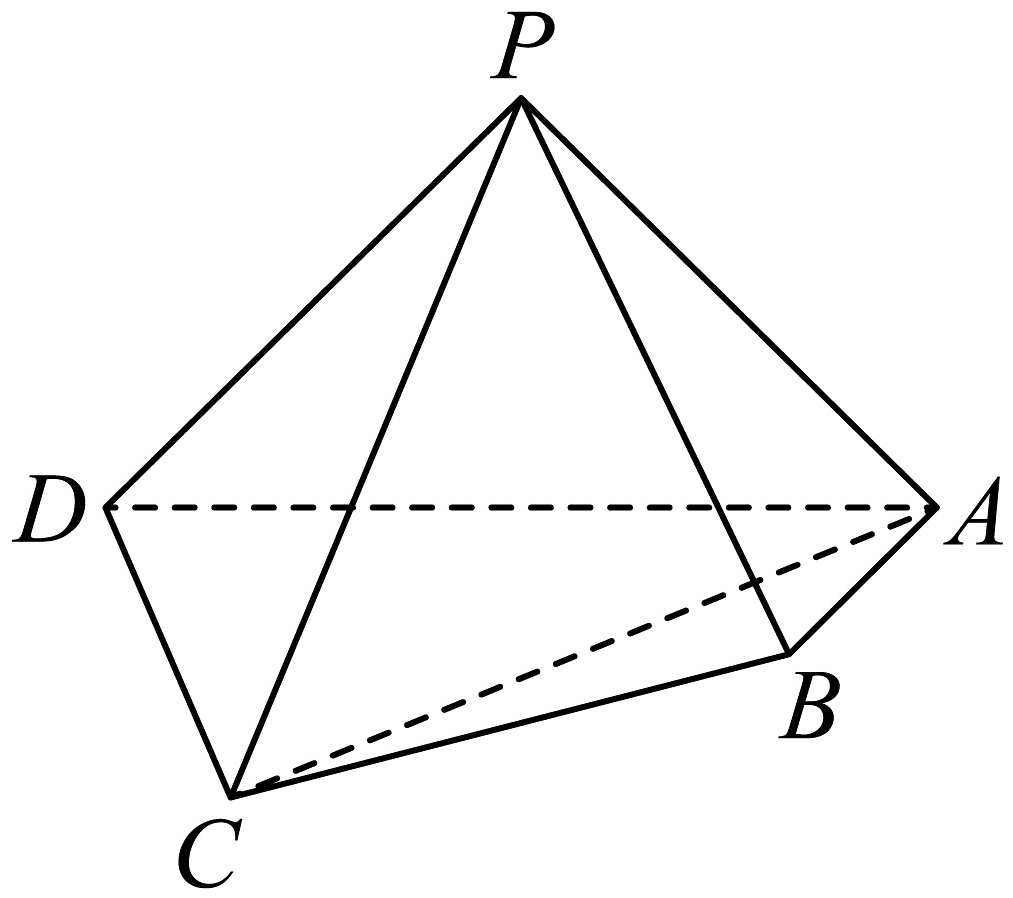 (1)、求证:平面平面;(2)、在棱上是否存在点 , 使得平面?若存在,求的值;若不存在,说明理由.
(1)、求证:平面平面;(2)、在棱上是否存在点 , 使得平面?若存在,求的值;若不存在,说明理由. -
18、设三个内角的对边分别为 , 且 , , 为锐角三角形,是边的中点,则的取值范围是 .
-
19、已知两平行直线的方向向量分别为 , , 则实数的值为 .
-
20、在棱长为的正方体中,已知分别为线段 , 的中点,点满足 , , , 则( )A、当时,三棱锥的体积为 B、当时,四棱锥外接球半径为 C、周长的最小值为 D、若 , 则点的轨迹长为