相关试卷
-
1、已知数列和满足 , , 且 , .(1)、求数列和的通项公式;(2)、求的值.(其中表示不大于的最大整数,如)
-
2、已知四棱锥 , 底面ABCD是直角梯形,侧面PAD是等边三角形, , , AD=2,BC=1, , M是PD的中点.
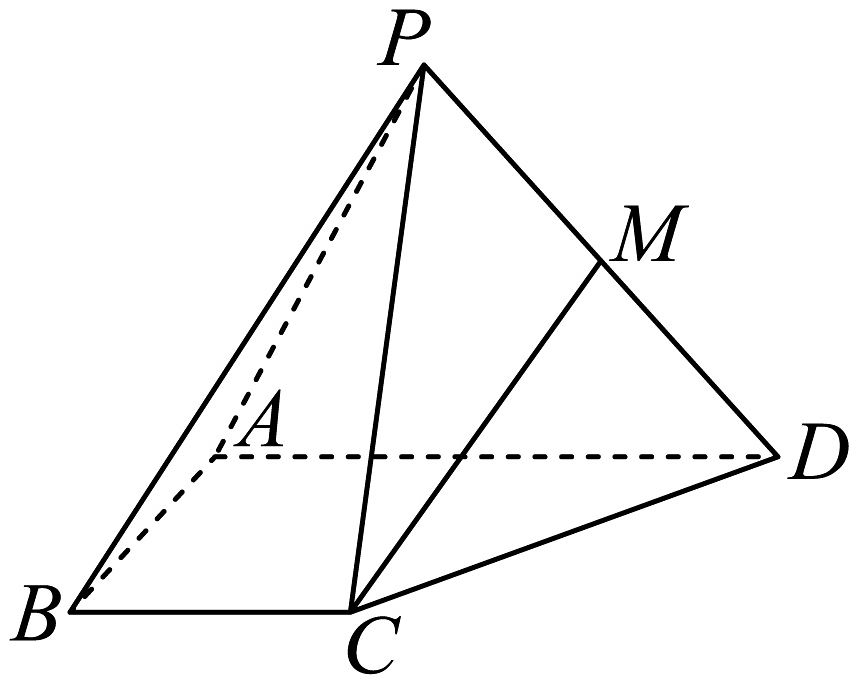 (1)、求证:直线平面;(2)、当二面角的大小为时,求直线CM与平面ABCD所成角的正弦值.
(1)、求证:直线平面;(2)、当二面角的大小为时,求直线CM与平面ABCD所成角的正弦值. -
3、某市为了推广垃圾分类,在全市范围内开展了一系列宣传活动.为了评估宣传效果,市环保部门随机抽取了1000名市民进行调查.假设该市成年人口为100万,且调查结果可以代表全市成年人口的情况.调查结果如右:
了解情况
非常了解
一般了解
不了解
人数(名)
580
320
100
(1)、从该市成年人口中随机抽取1人,求其对垃圾分类知识“不了解”的概率;(2)、该市环保部门计划对“不了解”垃圾分类知识的市民进行重点宣传.假设经过重点宣传后,“不了解”的市民中有50%转变为“一般了解”,有20%转变为“非常了解”,其余保持不变.经过重点宣传后,从该市成年人口中随机抽取3人,记X为其中对垃圾分类知识“非常了解”的人数,求X的分布列及数学期望. -
4、已知集合 , 含两个元素的集合 .
(1)若 , 则满足条件的集合A的个数为;
(2)若 , 则满足条件的不同的有序数对的个数为 . (结果均要化简)
-
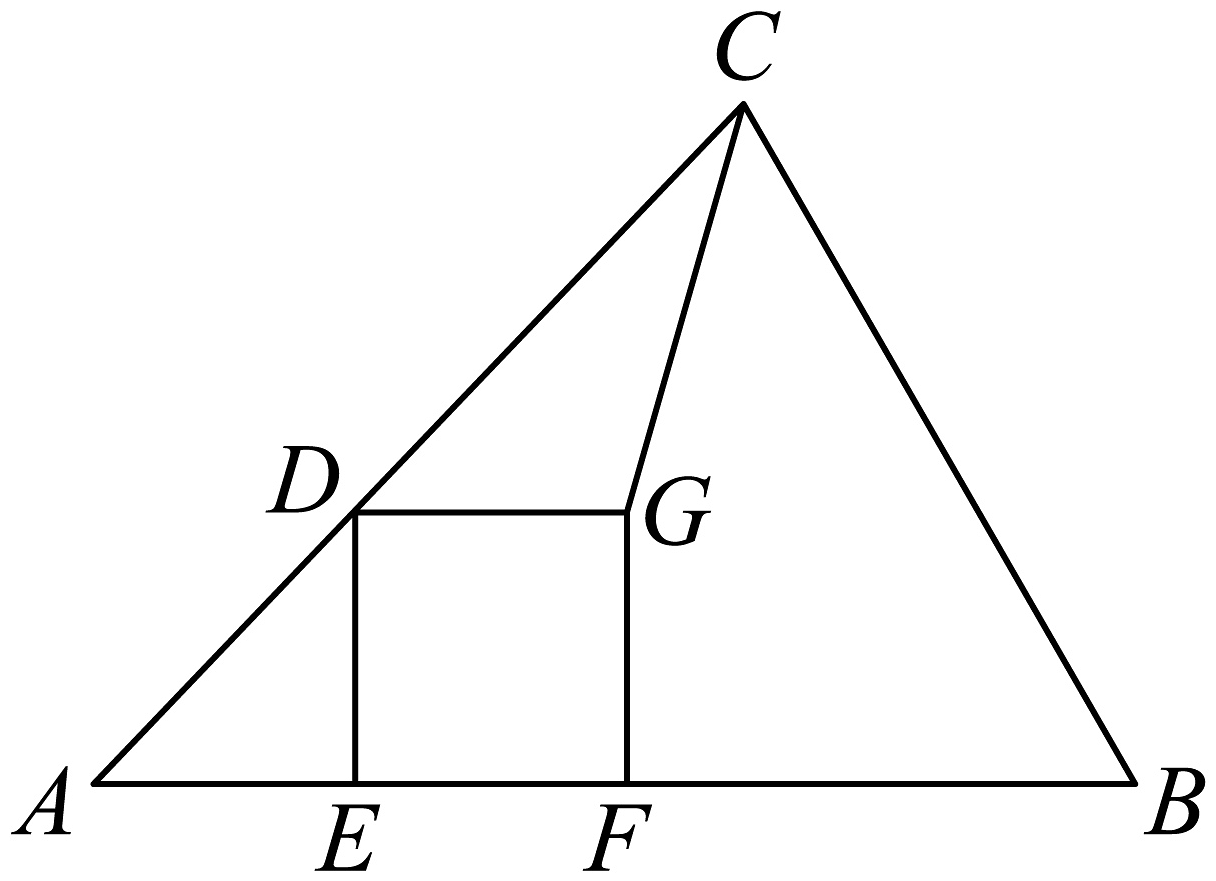
5、如图,已知在中, , , , 是线段上的动点,、是线段上的动点(在的右侧),且四边形是正方形,则线段长度的最小值是 .
-
6、已知 , , 则= .
-
7、如图,是由两个平行平面截半径为2cm且足够高的圆柱体所得的几何体,截面与圆柱体的轴成45°,上、下截面间的距离为.某高中数学兴趣小组对该几何体进行了探究,得出下列四个结论,其中正确的是( )
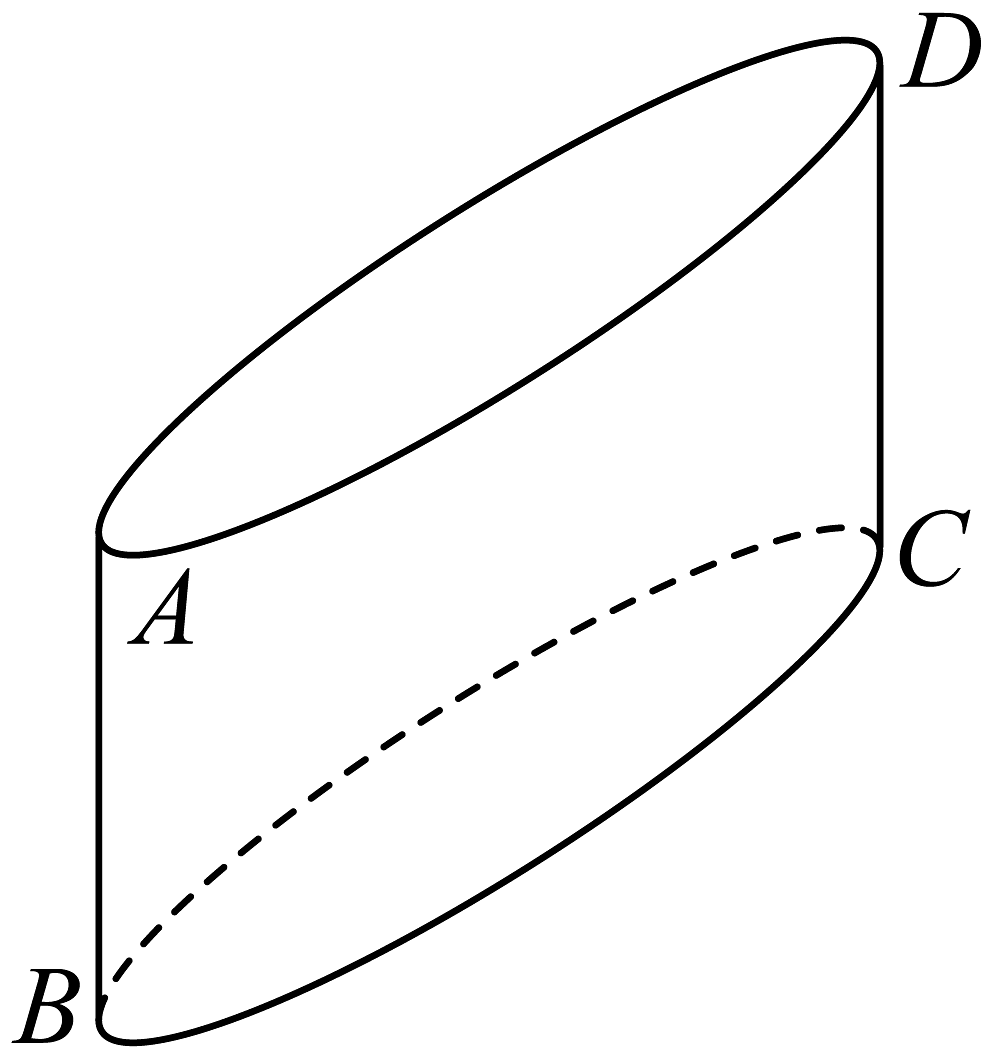 A、截口曲线的离心率为 B、该几何体的体积为 C、该几何体的侧面积为 D、该几何体的上截面面积为
A、截口曲线的离心率为 B、该几何体的体积为 C、该几何体的侧面积为 D、该几何体的上截面面积为 -
8、已知 , , , 则下列选项正确的是( )A、的取值范围是 B、的最大值为30 C、的最小值为 D、的最小值为
-
9、已知是定义域为R且周期为2的函数,其部分图象如图所示,则下列选项对恒成立的是( )
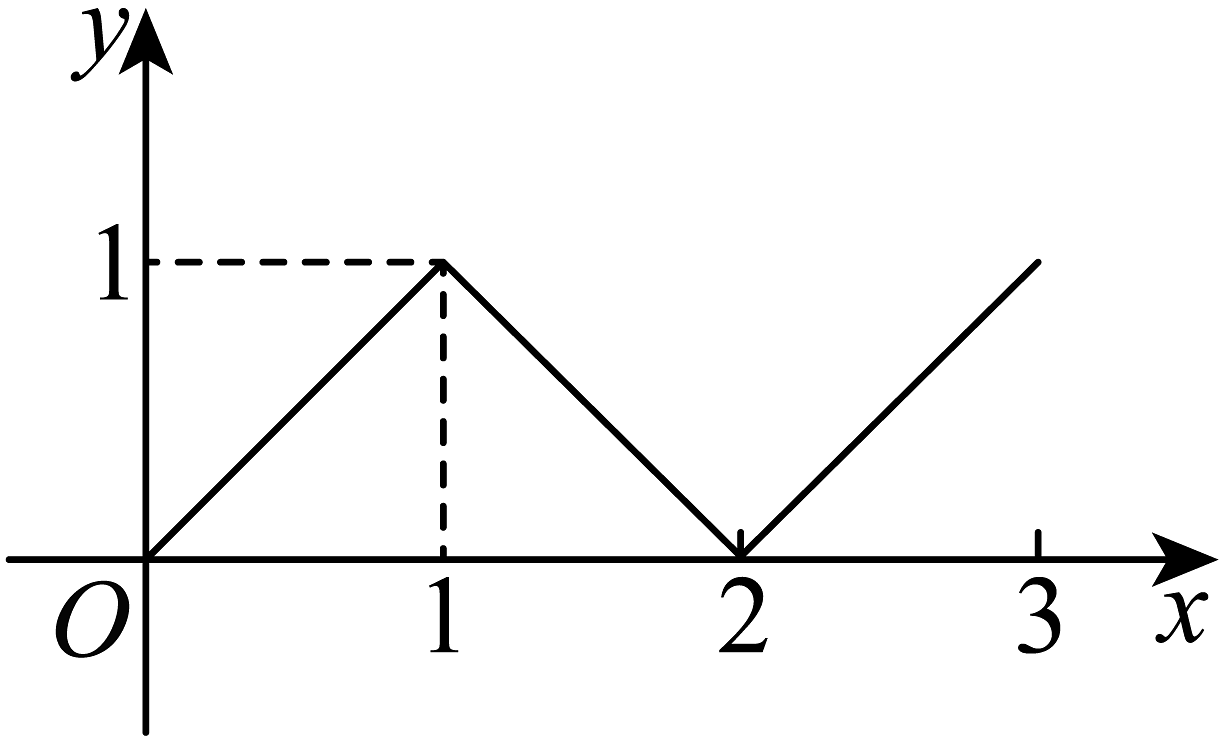 A、 B、 C、 D、
A、 B、 C、 D、 -
10、已知 , 为双曲线C:的左、右焦点,过作直线l与双曲线的右支交于A,B两点,且 , , 则双曲线C的离心率为( )A、 B、 C、 D、
-
11、已知某个正三棱台的上、下底面面积分别为和 , 高为6,则该正三棱台的外接球半径为( )A、4 B、 C、3 D、
-
12、已知一个盒子里有4个大小形状完全相同的小球,其中2个红球,2个黑球,现从中任取两球,若已知一个是红球,则另一个也是红球的概率是( )A、 B、 C、 D、
-
13、已知复数 , ( , i为虚数单位),则“”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
14、若随机变量 , 且 , 则( )A、 B、 C、 D、
-
15、已知等差数列的公差 , , 则的最小值为( )A、1 B、2 C、3 D、4
-
16、已知圆M: , 则圆心坐标和半径分别为( )A、 , 4 B、 , 4 C、 , 2 D、 , 2
-
17、从稻田中随机抽取7株水稻苗,测得苗高(单位:)分别是.则这组数据的众数和中位数分别是( )A、24,25 B、23,23 C、23,24 D、24,24
-
18、已知平面向量是两个单位向量,在上的投影向量 , 则( )A、1 B、 C、 D、
-
19、已知是公差不为0的无穷等差数列.若对于中任意两项 , , 在中都存在一项 , 使得 , 则称数列具有性质.(1)、已知 , , 判断数列 , 是否具有性质;(2)、若数列具有性质 , 证明:的各项均为整数;(3)、若 , 求具有性质的数列的个数.
-
20、已知椭圆的焦距为 , 离心率为.(1)、求椭圆的方程;(2)、设过点且斜率为的直线与椭圆交于不同的两点、 , 点在以线段为直径的圆外(为原点),求的取值范围.