相关试卷
-
1、已知分别是双曲线的左、右焦点,为左顶点,是双曲线在第四象限上一点,的斜率为 , 且 , 则双曲线的离心率为( )A、2 B、 C、3 D、
-
2、已知数列的前项和为 , 则下列说法正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
3、已知非零向量满足 , 则在方向上的投影向量为( )A、 B、 C、 D、
-
4、尽管目前人类还是无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震时释放出的能量(单位:焦耳)与地震里氏震级之间的关系为:.若记2025年1月7日西藏日喀则发生里氏6.8级地震释放出来的能量为 , 2022年5月20日四川雅安发生里氏4.8级地震释放出来的能量为 , 则( )A、 B、 C、 D、
-
5、“”是“直线与圆相切”的( )A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件
-
6、已知复数满足为虚数单位 , 则( )A、2 B、 C、1 D、
-
7、已知集合 , 则( )A、 B、 C、 D、
-
8、将所有正整数按照如下规律形成数阵:
第1行 1 2 3 …… 7 8 9
第2行 10 11 12 …… 97 98 99
第3行 100 101 102 …… 997 998 999
第4行 1000 1001 1002 …… 9997 9998 9999
…………
(1)、将数列与数列的公共项按照从小到大的顺序排列得到数列 , 试确定在该数阵中的位置;(2)、将数阵中所有相邻两位数字(从左到右)出现12的所有正整数去掉并保持顺序不变,得到一个新数阵,记新数阵第行中正整数的个数为.(i)求 , , ;
(ii)求.
-
9、已知函数 , .(1)、讨论零点的个数;(2)、若 , 求实数的取值范围.
-
10、如图,在四棱锥中,底面为矩形,为的中点, , .
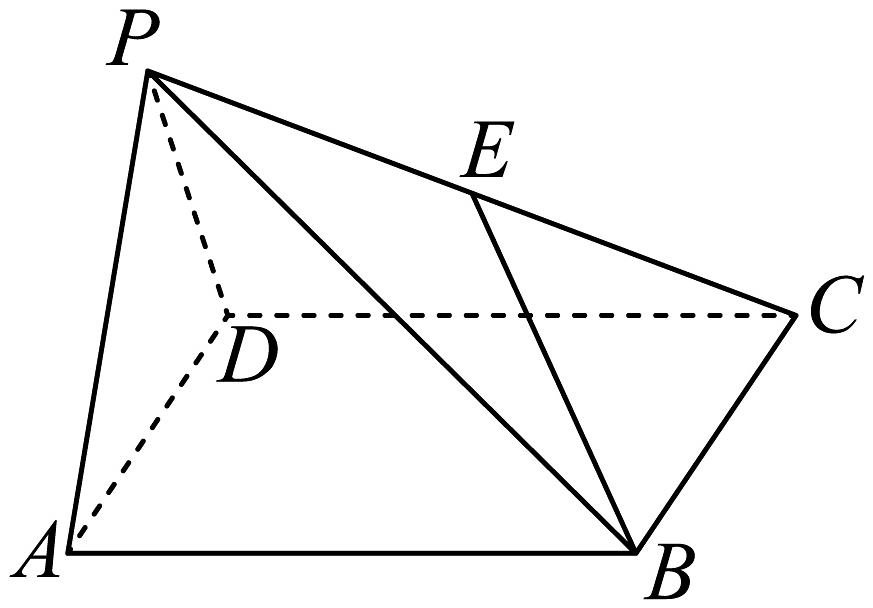 (1)、证明:平面平面;(2)、若 , 直线与平面所成角的正切值等于2,求平面与平面夹角的余弦值.
(1)、证明:平面平面;(2)、若 , 直线与平面所成角的正切值等于2,求平面与平面夹角的余弦值. -
11、已知抛物线上一点到其焦点的距离为4.(1)、求拋物线的方程;(2)、已知抛物线的准线为为坐标原点,若过焦点的动直线与抛物线交于两点,直线AO与交于点 ,
(i)证明:直线轴;
(ii)过两点分别作抛物线的切线相交于点且分别与直线相交于点 , 求面积的取值范围.
-
12、如图,矩形ABCD中, . 现以EF为折痕把四边形ABFE折起得到平面 , 并连接 .
 (1)、若 , 证明:平面BEF;(2)、若为的中点, , 直线GE与平面所成角正弦值为 .
(1)、若 , 证明:平面BEF;(2)、若为的中点, , 直线GE与平面所成角正弦值为 .(i)试讨论在线段AD上是否存在点 , 使得平面GMN.若存在,请求出DN的长度;若不存在,请说明理由;
(ii)求平面与平面所成锐二面角的取值范围.
-
13、已知函数在点处的切线与曲线只有一个公共点.(1)、求的值;(2)、求证: .
-
14、已知数列中, , .(1)、证明:数列为等比数列;(2)、求数列的通项公式;(3)、记数列的前项和为 , 若对任意恒成立,求实数的取值范围.
-
15、为了更好地了解中学生的体育锻炼时间,某校展开了一次调查,从全校学生中随机选取人,统计了他们一周参加体育锻炼时间(单位:小时),分别位于区间 , , 用频率分布直方图表示如下图.假设用频率估计概率,且每个学生参加体育锻炼时间相互独立.
 (1)、求的值;(2)、估计全校学生一周参加体育锻炼时间的第百分位数;(3)、从全校学生中随机选取人,记表示这人一周参加体育锻炼时间在区间内的人数,求的分布列和数学期望 .
(1)、求的值;(2)、估计全校学生一周参加体育锻炼时间的第百分位数;(3)、从全校学生中随机选取人,记表示这人一周参加体育锻炼时间在区间内的人数,求的分布列和数学期望 . -
16、的展开式中项的系数为 .
-
17、已知且 , 若 , 则 .
-
18、甲、乙两人轮流掷一枚质地均匀的骰子,甲先掷.下列选项中正确的是( )A、“甲第一次掷骰子掷出偶数点”的概率为 B、“在甲掷出点后,乙下一次掷骰子掷出点”的概率为 C、“首次连续次出现点时需掷骰子的次数”的期望为 D、“甲先掷出点”的概率为
-
19、已知椭圆 , 直线与椭圆相交于两点,若椭圆上存在异于两点的点使得 , 则离心率的值可以为( )A、0.8 B、0.85 C、0.9 D、0.95
-
20、双曲三角函数是一类与常见圆三角函数相似但具有独特性质的函数,主要包括双曲余弦函数、双曲正弦函数、双曲正切函数 , 则( )A、是偶函数 B、是奇函数 C、是偶函数 D、是奇函数