相关试卷
-
1、圆与的公共弦长为( )A、 B、 C、 D、4
-
2、设为等差数列,且 , 则( )A、16 B、18 C、20 D、22
-
3、若直线的倾斜角的大小为 , 则实数( )A、 B、 C、 D、
-
4、已知 , , 且 , 则( )A、-6 B、5 C、4 D、6
-
5、交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙三个社区做分层抽样调查.假设三个社区驾驶员的总人数为 , 其中甲社区有驾驶员96人.若在甲、乙、丙三个社区抽取驾驶员的人数分别为16,20,26,则这三个社区驾驶员的总人数为( )A、744 B、620 C、372 D、162
-
6、在国务院新闻办公室举行的“推动高质量发展”系列主题新闻发布会上,教育部相关负责人表示,要在关键环节方面,让“健康第一”落细落地.实施学生体质强健计划、心理健康促进行动等,保障中小学生每天综合体育活动时间不低于2小时,全面培育学生积极心理品质.要让孩子们动起来、互动起来,多见阳光,多呼吸新鲜空气.(1)、为了解喜爱排球运动是否与性别有关,某统计部门在某地随机抽取了男性和女性各100名进行调查,得到列联表如下:
喜爱排球运动
不喜爱排球运动
合计
男性
60
40
100
女性
45
55
100
合计
105
95
200
依据小概率值的独立性检验,能否认为喜爱排球运动与性别有关?
(2)、某校排球队的甲、乙、丙、丁四名球员进行传球训练,甲等可能地随机传向另外3人中的1人,乙也等可能地随机传向另外3人中的1人,丙、丁均等可能地随机传向甲、乙中的1人,第1次由甲将球传出,如此不停地传下去,且假定每次传球都能被接到.记第n次传球之后球在丙或丁手上的概率为 .(ⅰ)计算 , , 并求的通项公式;
(ⅱ)记第n次传球之后球在乙手上的概率为 , 求的通项公式.
附:
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
-
7、设a为实数,函数 .(1)、若曲线过点 , 求a的值;(2)、当时,求的最小值;(3)、若恰有两个极值点,求a的取值范围.
-
8、已知是抛物线上的点,到抛物线的焦点的距离为 .(1)、求的方程;(2)、若直线与交于 , 两点,且(点为坐标原点),求面积的最小值.
-
9、如图,在四棱锥中,底面ABCD为菱形, , .
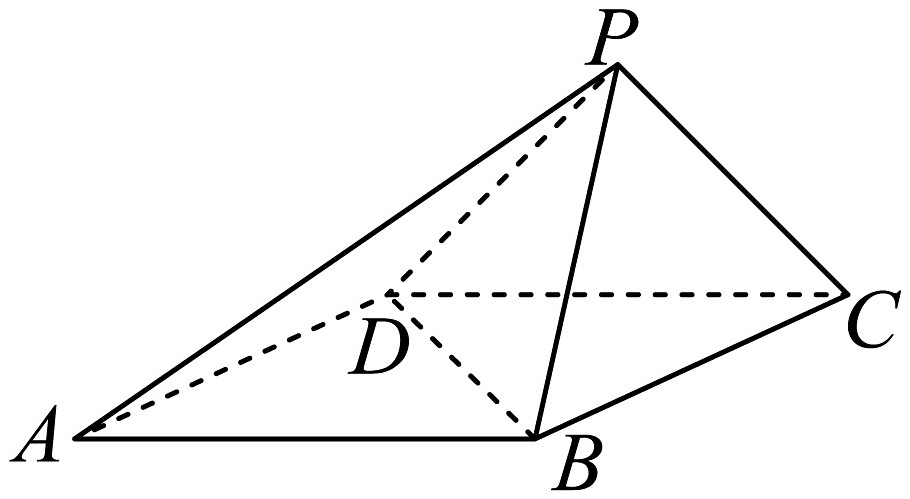 (1)、证明:;(2)、若 , , 求二面角的余弦值.
(1)、证明:;(2)、若 , , 求二面角的余弦值. -
10、记的内角A,B,C的对边分别为a,b,c,已知 .(1)、求C;(2)、若外接圆的半径为1,求面积的最大值.
-
11、已知集合 , 则满足的有序集组的个数为 . (用数字作答)
-
12、点M在椭圆上,F是椭圆的一个焦点,N为MF的中点,O为坐标原点, , 则 .
-
13、函数的图象在点处的切线的斜率为 .
-
14、已知 , 则( )A、的最小值是 B、的最小值是 C、的最小值是 D、的最大值是
-
15、下列说法正确的有( )A、这组数据的第百分位数是 B、若一组数据 , , …,的方差为 , 则 , , …,的方差为1 C、若变量服从二项分布 , 则 D、若变量服从正态分布 , , 则
-
16、已知 , , 曲线与曲线无公共点,则曲线的离心率的取值范围为( )A、 B、 C、 D、
-
17、已知函数在上有且仅有2个零点,则实数m的取值范围是( )A、 B、 C、 D、
-
18、已知函数是定义域为的奇函数,当时, . 若 , , 则a的取值范围为( )A、 B、 C、 D、
-
19、某圆锥母线长为1,其侧面积与轴截面面积的比值为 , 则该圆锥的高为( )A、 B、1 C、2 D、
-
20、设等差数列的公差为d,若 , , 则( )A、1 B、2 C、3 D、4