相关试卷
-
1、已知函数 .(1)、当时,求的单调减区间;(2)、若 , , 证明:;(3)、若 , 恒有 , 求实数的取值范围.
-
2、已知点 , 曲线上的点与两点的连线的斜率分别为和 , 且 .(1)、求曲线的方程;(2)、是否存在一条直线与曲线交于两点,以为直径的圆经过坐标原点 . 若存在,求出的值;若不存在,请说明理由.
-
3、已知函数.(1)、求函数的单调递增区间;(2)、若 , , 求的值.
-
4、如图,已知 , 为边上的两点,且满足 , 则当取最大值时,的面积等于.
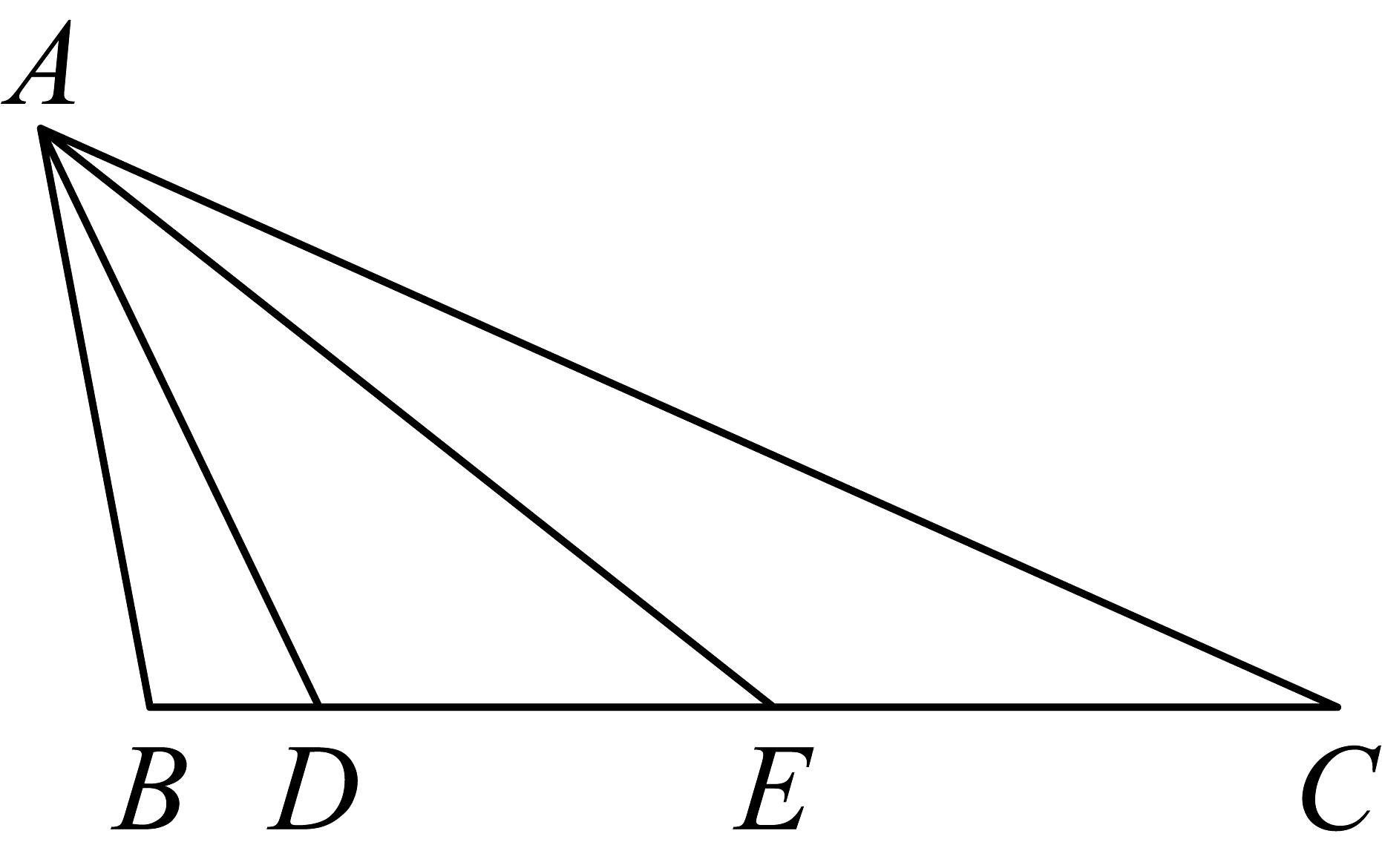
-
5、若在上单调递减,则实数的取值范围为 .
-
6、已知随机变量 , 若 , 则 .
-
7、已知数列是公比为的等比数列,且 , 则下列叙述中正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 且 , 则
-
8、如图抛物线的顶点为 , 焦点为 , 准线为 , 焦准距为;抛物线的顶点为 , 焦点也为 , 准线为 , 焦准距为 . 和交于两点,分别过作直线与两准线垂直,垂足分别为 , 过的直线与封闭曲线交于两点,则下列说法正确的是( )
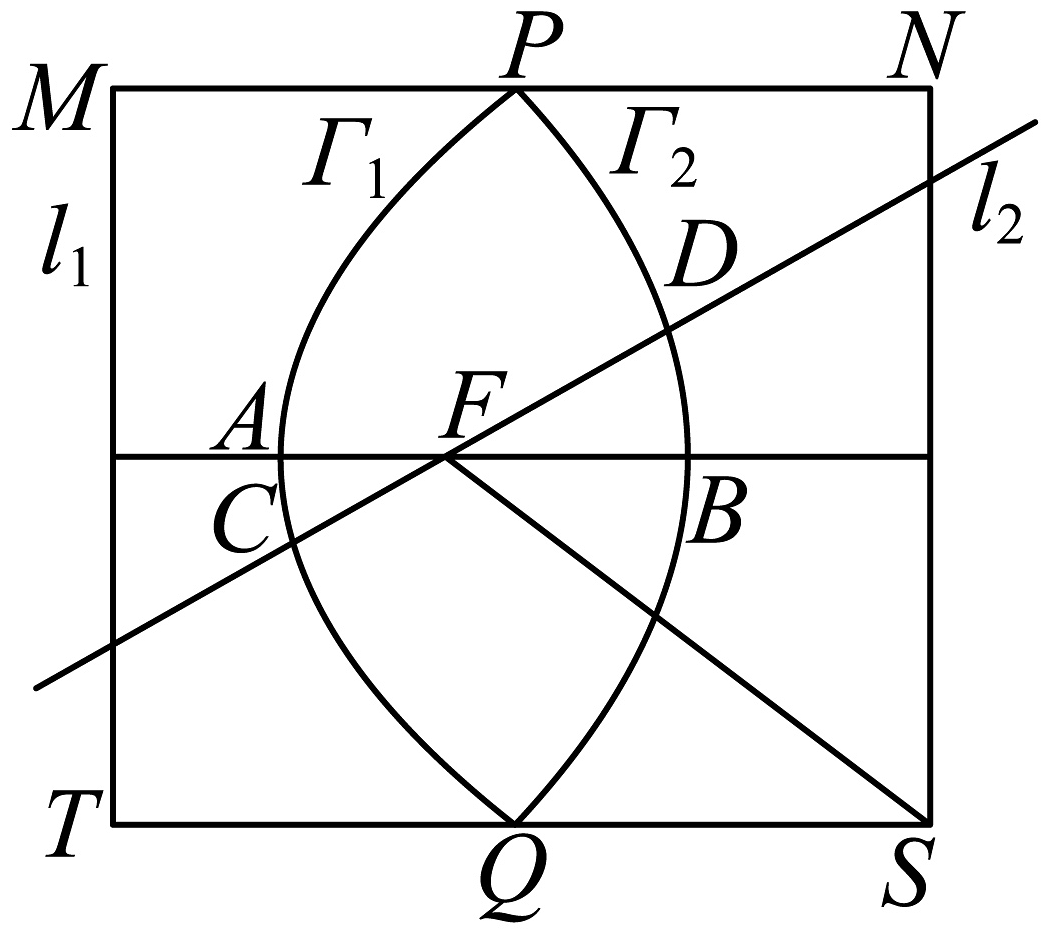 A、 B、四边形的面积为 C、 D、的取值范围为
A、 B、四边形的面积为 C、 D、的取值范围为 -
9、已知 , 且 , 其中为自然对数的底数,则下列结论正确的是( )A、 B、 C、 D、
-
10、方程在上的实数解有( )A、0个 B、1个 C、2个 D、3个
-
11、已知长方体 , 是棱的中点,平面将长方体分割成两部分,则体积较大部分与体积较小部分的体积之比为( )A、 B、 C、 D、
-
12、若 , , 下列正确的是( )A、 B、 C、方向上的投影向量是 D、
-
13、若直线与双曲线有两个不同交点,则的取值范围是( )A、 B、 C、 D、
-
14、若复数的实部大于0,且 , 则( )A、 B、 C、 D、
-
15、已知集合 , , 则( )A、 B、 C、 D、
-
16、已知函数 .(1)、若 , 求在的值域;(2)、证明:存在唯一的极值点 , 且;(3)、若恒成立,证明: .
-
17、甲、乙两选手进行象棋比赛,假设每局比赛结果相互独立,且每局比赛甲获胜的概率为 , 乙获胜的概率为 .(1)、若比赛采用三局两胜制,求甲获胜的概率;(2)、如果比赛采用五局三胜制(当一队赢得三场胜利时,该队获胜,比赛结束)进行比赛,求比赛的局数X的分布列和期望;(3)、如果每局比赛甲获胜的概率为 , 乙获胜的概率为 , 比赛的赛制有五局三胜制和三局两胜制两种选择,请问对于甲选手来说,该如何选择比赛赛制对自己更有利,请说明理由,由此你能得出什么结论.
-
18、已知角的终边过点 , 则 .
-
19、如图,在四棱锥中, , .现设.
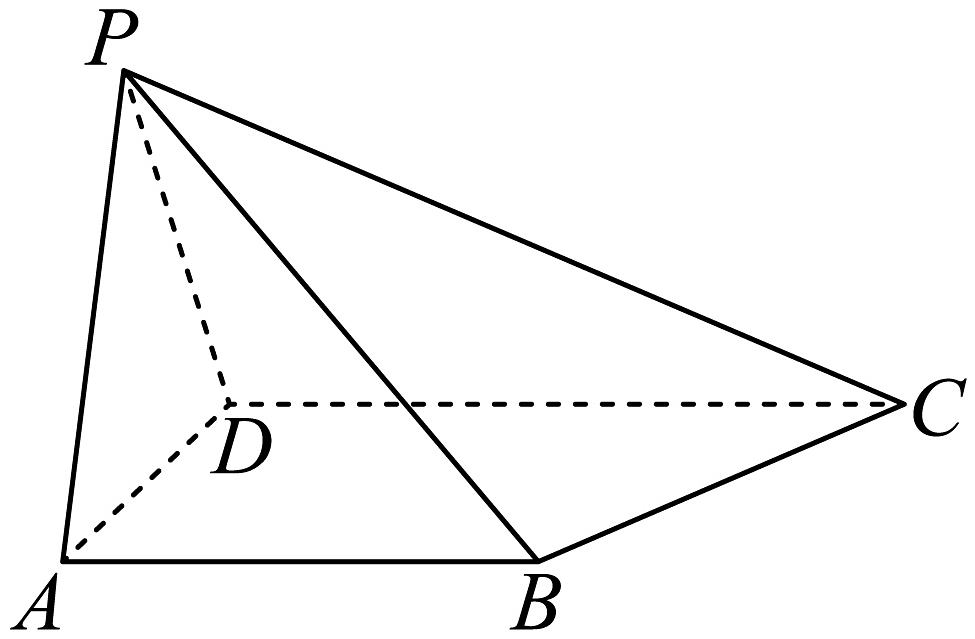 (1)、求证:平面平面;(2)、当时,侧棱PC上点M满足 , 证明:M是侧棱的中点;(3)、当时,求三棱锥的外接球体积的最小值.
(1)、求证:平面平面;(2)、当时,侧棱PC上点M满足 , 证明:M是侧棱的中点;(3)、当时,求三棱锥的外接球体积的最小值. -
20、已知向量 , , 设函数.(1)、化简并写出的最小正周期;(2)、若 , 且 , 求的值;(3)、在锐角中,若 , , 求周长的取值范围.