相关试卷
-
1、已知长方体 , 是棱的中点,平面将长方体分割成两部分,则体积较大部分与体积较小部分的体积之比为( )A、 B、 C、 D、
-
2、若 , , 下列正确的是( )A、 B、 C、方向上的投影向量是 D、
-
3、若直线与双曲线有两个不同交点,则的取值范围是( )A、 B、 C、 D、
-
4、若复数的实部大于0,且 , 则( )A、 B、 C、 D、
-
5、已知集合 , , 则( )A、 B、 C、 D、
-
6、已知函数 .(1)、若 , 求在的值域;(2)、证明:存在唯一的极值点 , 且;(3)、若恒成立,证明: .
-
7、甲、乙两选手进行象棋比赛,假设每局比赛结果相互独立,且每局比赛甲获胜的概率为 , 乙获胜的概率为 .(1)、若比赛采用三局两胜制,求甲获胜的概率;(2)、如果比赛采用五局三胜制(当一队赢得三场胜利时,该队获胜,比赛结束)进行比赛,求比赛的局数X的分布列和期望;(3)、如果每局比赛甲获胜的概率为 , 乙获胜的概率为 , 比赛的赛制有五局三胜制和三局两胜制两种选择,请问对于甲选手来说,该如何选择比赛赛制对自己更有利,请说明理由,由此你能得出什么结论.
-
8、已知角的终边过点 , 则 .
-
9、如图,在四棱锥中, , .现设.
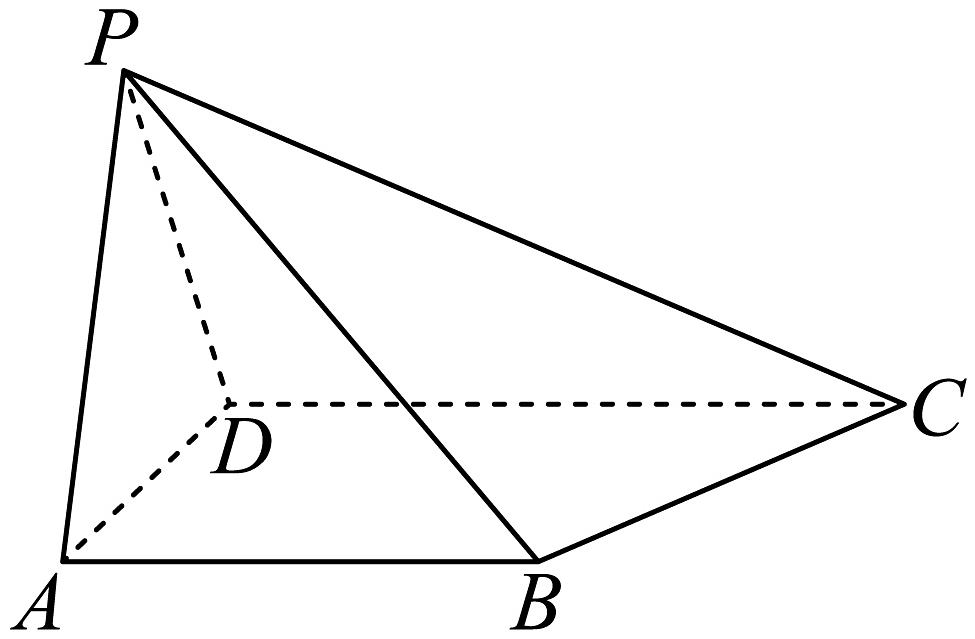 (1)、求证:平面平面;(2)、当时,侧棱PC上点M满足 , 证明:M是侧棱的中点;(3)、当时,求三棱锥的外接球体积的最小值.
(1)、求证:平面平面;(2)、当时,侧棱PC上点M满足 , 证明:M是侧棱的中点;(3)、当时,求三棱锥的外接球体积的最小值. -
10、已知向量 , , 设函数.(1)、化简并写出的最小正周期;(2)、若 , 且 , 求的值;(3)、在锐角中,若 , , 求周长的取值范围.
-
11、2025年六五环境日主题为“美丽中国我先行”,南京市某社区举办“环保我参与”有奖问答比赛活动.某场比赛中,甲、乙、丙三个家庭同时回答一道有关环保知识的问题.已知甲家庭回答这道题正确的概率是 , 甲、乙两个家庭都回答正确的概率是 , 乙、丙两个家庭至少一家回答正确的概率是.各家庭回答是否正确相互独立.(1)、求乙、丙两个家庭各自回答这道题正确的概率;(2)、求甲、乙、丙三个家庭中不少于2个家庭回答这道题正确的概率.
-
12、如图,在直三棱柱中,已知 , , 设的中点为D,的中点为E.求证:
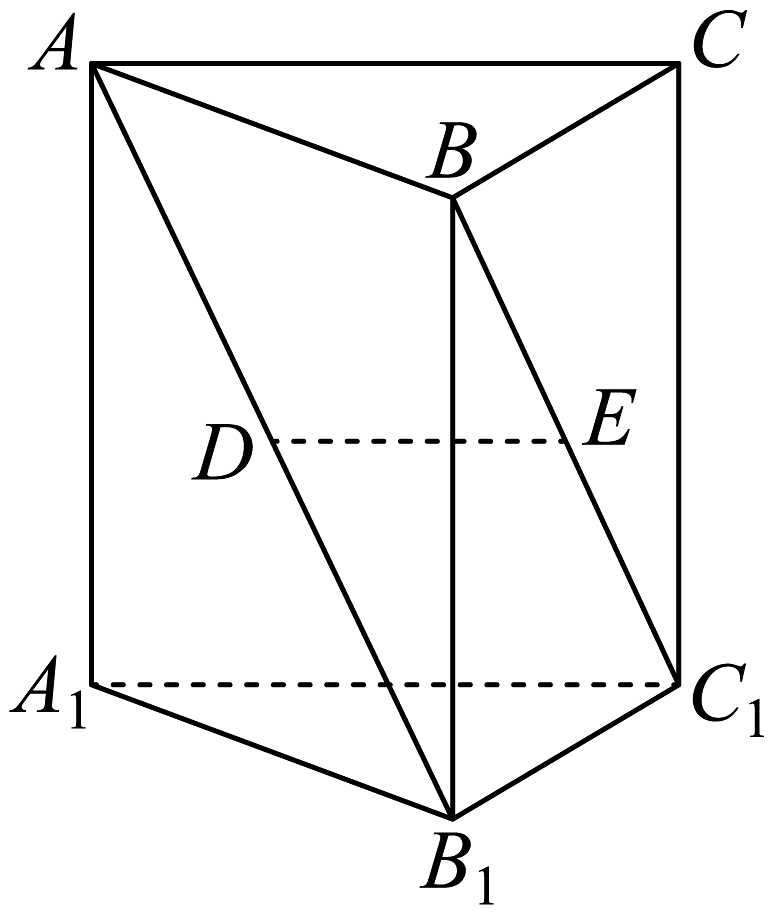 (1)、平面;(2)、.
(1)、平面;(2)、. -
13、已知复数(),且为纯虚数(是的共轭复数).(1)、设复数 , 求;(2)、复数在复平面内对应的点在第一象限,求实数的取值范围.
-
14、已知 , 平面上动点满足对任意恒成立,则的最小值为 , 此时.
-
15、已知60个样本数据的平均数为3,其中 , 则这60个数据的方差为.
-
16、在正四棱台中, , , , 则该棱台的体积 .
-
17、已知正方体的棱长为2,点为线段上的动点,则( )A、的最小值为 B、与始终保持垂直 C、以为球心,为半径的球面与平面的交线长为 D、经过的平面截正方体所得截面面积的最小值为
-
18、已知数据 , …,的众数、平均数、方差、第80百分位数分别是 , , , , 数据 , , , …,的众数、平均数、方差、第80百分位数分别是 , , , , 且满足 , 则下列结论正确的是( )A、 B、 C、 D、
-
19、正多面体被古希腊圣哲认为是构成宇宙的基本元素,加上它们的多种变体,一直是科学、艺术、哲学灵感的源泉之一.如图,一个正八面体八个面分别标有数字1到8,任意抛掷一次这个正八面体,观察它与地面接触的面上的数字,得到样本空间为 , 记“得到的点数为奇数”为事件A,记“得到的点数不大于4”为事件B,记“得到的点数为质数”为事件C,则下列说法正确的是( )
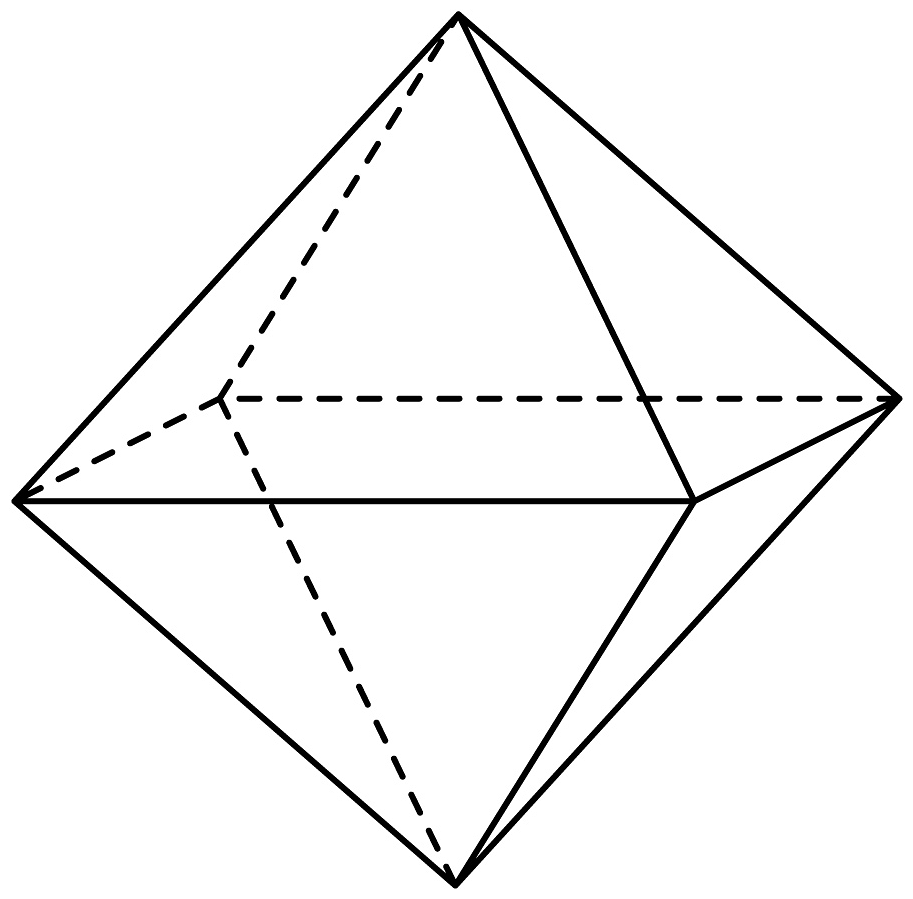 A、事件与互斥 B、 C、事件与相互独立 D、
A、事件与互斥 B、 C、事件与相互独立 D、 -
20、中,角A、B、C的对边分别为、、 , 满足 , 若存在最小值,则实数的取值范围是( )A、 B、 C、 D、