相关试卷
-
1、科技创新成为全球经济格局关键变量,某公司为实现1600万元的利润目标,准备制定一个激励研发人员的奖励方案:当投资收益达到600万元时,按投资收益进行奖励,要求奖金(单位:万元)随投资收益(单位:万元)的增加而增加,奖金总数不低于20万元,且奖金总数不超过投资收益的.(1)、现有①;②;③三个奖励函数模型.结合函数的性质及已知条件.当时,判断哪个函数模型符合公司要求?(2)、根据(1)中符合公司要求的函数模型,要使奖金达到50万元,公司的投资收益至少为多少万元?
-
2、若实数x,y满足 , , 则的取值范围是.
-
3、设是平面,m,n是两条直线,则下列命题正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若与所成的角相等,则
-
4、已知函数 在上具有单调性,则实数的取值范围 .
-
5、张景中院士在《与中学教师谈微积分》一文中,给出了“差商有界”函数和“广义差商有界”函数的定义, 即若函数 在区间 上有定义,并且存在一个正数 ,使得 且 ,不等式 恒成立,则称 在 上为“差商有界”函数;若函数 在区间 上有定义,并且存在一个正整数 ,使得 且 ,不等式 恒成立,则称 在 上为 “广义差商有界”函数.(1)、已知 ,判断 在区间 上是否是“差商有界”函数?若是,请说明理由;若不是,请讨论是否是“广义差商有界”函数?(2)、已知函数 .
(i)判断 在区间 上是否是“差商有界”函数?并说明理由;
(ii)若 在区间 上是“广义差商有界”函数,求正整数 的最小值.
-
6、下列命题正确的是( )A、若向量共线,则必在同一条直线上 B、若为平面内任意三点,则 C、若点为的重心,则 D、已知向量 , 若 , 则
-
7、已知函数 , 且 , .(1)、求的解析式;(2)、判断在上的单调性,并用定义证明.(3)、若对 , 恒成立,求实数的取值范围.
-
8、已知是等差数列,且 , , 数列是等比数列,其前n项和为 , 且满足 , 其中.(1)、当时,求数列与数列的通项公式;(2)、在(1)的条件下,设数列的前n项和为 , 已知 , 证明:;(3)、当时,若数列满足(),且 , 若对任意正整数i,j(),恒成立,求实数的取值范围.
-
9、在平面直角坐标系xOy中,动点()到点的距离与到x轴的距离之差等于1,记动点P的轨迹为.(1)、求轨迹的方程;(2)、过直线l:上一点Q作轨迹的两条切线,切点分别为A,B.证明:直线AB过定点,并求出定点坐标;(3)、过点的动直线与轨迹交于C,D两点,直线CF交轨迹于另一点E,记△CDE,△CFR的面积分别为 , , 求的最小值.
-
10、已知函数 , 其中为常实数.(1)、当时,讨论函数在其定义域内的单调性;(2)、若是函数的极大值点,证明:.
-
11、在如图所示的多面体中,已知四边形为菱形,其对角线和相交于H点,G是棱的中点, , 且.
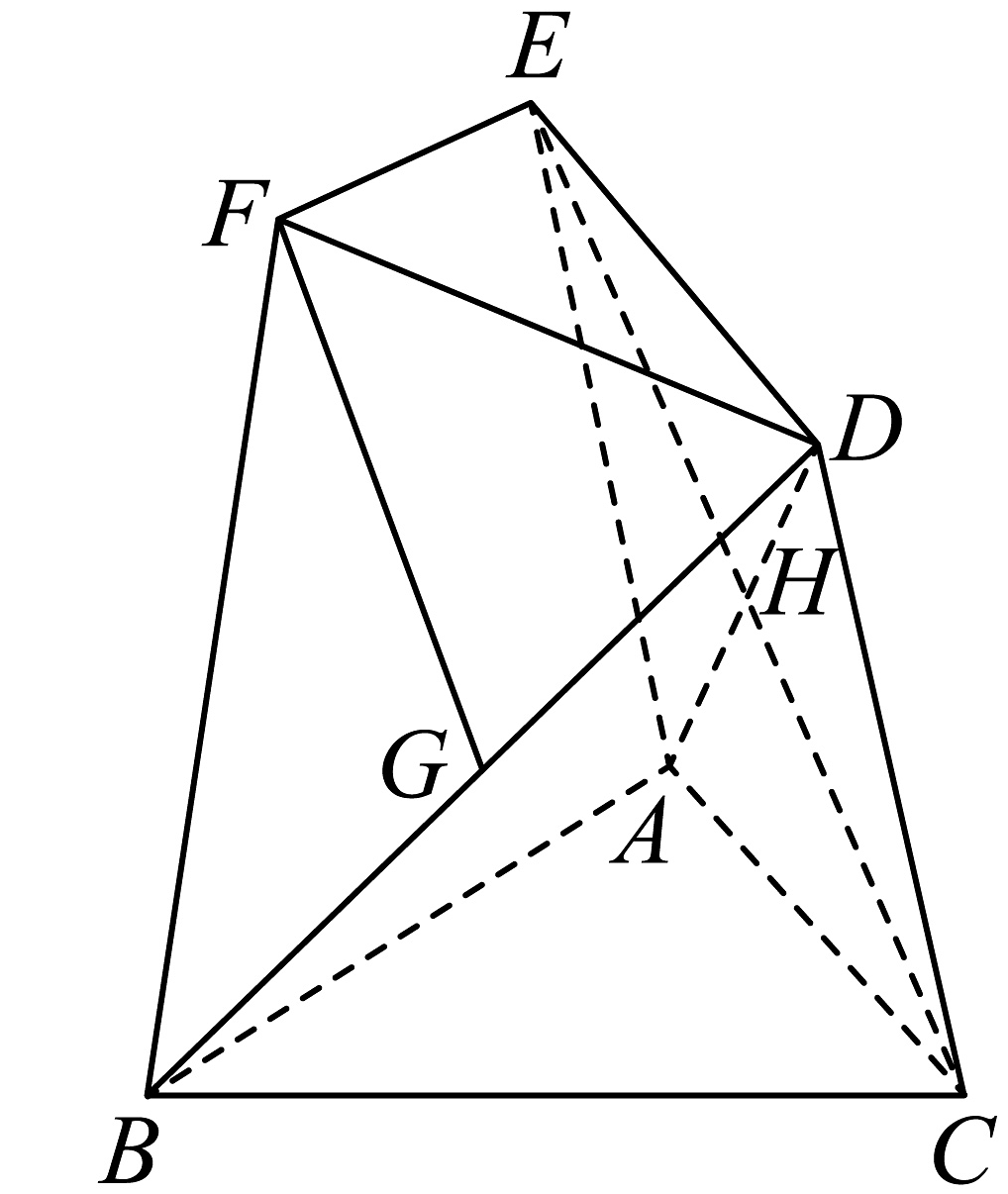 (1)、求证:平面;(2)、若平面 , , 求平面与平面所成角的余弦值.
(1)、求证:平面;(2)、若平面 , , 求平面与平面所成角的余弦值. -
12、我国新能源汽车的卓越性能赢得全球人民的信赖,某品牌新能源汽车凭借科研创新、广告宣传和可靠售后保障,在全球赢得了很好的营销局面.下表为2017年—2024年(年份代码分别记为:1,2,3,4,5,6,7,8)该品牌新能源汽车的科研经费投入和全球市场规模统计.
年份代码i
1
2
3
4
5
6
7
8
科研经费(单位:百亿元)
2
3
6
10
13
15
18
21
市场规模(单位:百万辆)
1
1
2
2.5
3.5
3.5
4.5
6
参考数据: , , , .
参考公式:相关系数.
(1)、根据样本数据,推断两个变量是否线性相关,并计算样本相关系数,推断它们的线性相关程度(结果精确到0.01,当越接近1时,成对样本数据的线性相关程度越强;当越接近0时,成对样本数据的线性相关程度越弱);(2)、已知在国内,新能源车主购买的新能源汽车为该品牌新能源汽车的概率为p(),从国内新能源车主中随机抽取5人,记这5人中选择购买该品牌的人数为随机变量X,若 , 求随机变量X的数学期望和方差 -
13、某无人机爱好者在年春节,设计了利用红、橙、黄、绿、紫五种颜色的无人机群呈现如图的方形阵,方形阵分为六个区域,呈现要求是:同一区域为相同颜色的无人机群,且相邻区域的无人机群颜色不能相同,区域必须是红色无人机群,则不同的呈现方式共有种.

-
14、如图,在直三棱柱中,△ABC是正三角形,D为AC的中点,点E在棱上,且 , 若 , , 则点到平面BDE的距离为.
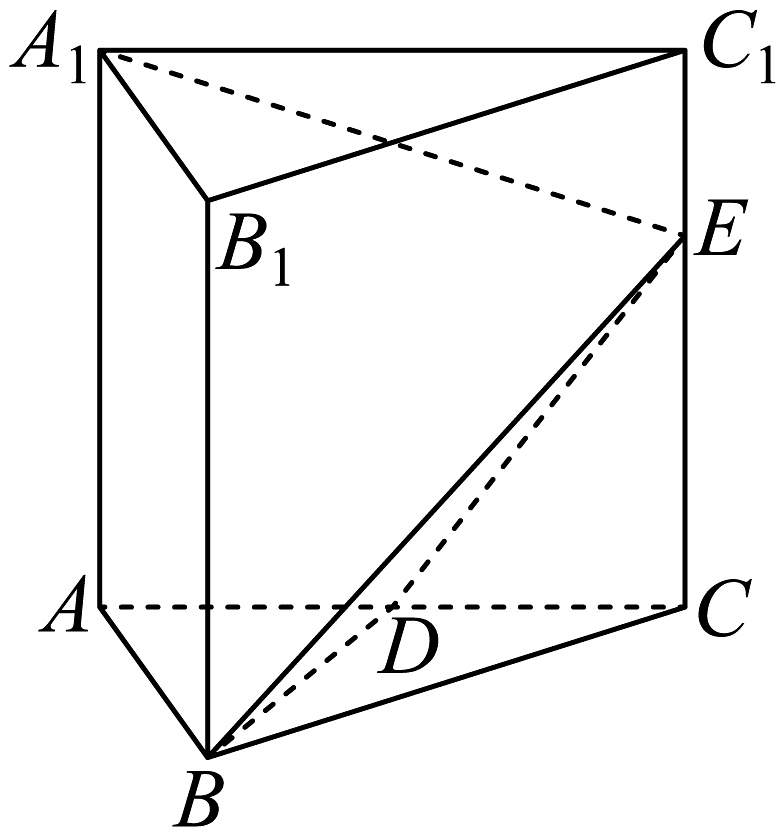
-
15、已知函数 , 则曲线在点处的切线方程为.
-
16、若函数满足:对任意 , 恒有 , 则称函数为“类余弦型”函数.已知函数为“类余弦型”,若 , 且对任意非零实数 , .则下列结论正确的是( )A、 B、若 , 则 C、函数为偶函数 D、若有理数 , 满足 , 则
-
17、已知椭圆C:()的左、右焦点分别为 , , , 离心率为 , 直线l过点与椭圆C交于M,N两点,若x轴上存在一定点P,使得的内切圆圆心在x轴上.则下列结论正确的有( )A、椭圆C的方程为 B、的周长为4 C、定点P的坐标为 D、当轴时,的内切圆圆心坐标为
-
18、将函数的图象沿x轴向右平移个单位长度,得到函数的图象,则下列结论正确的是( )A、 B、函数的最小正周期为 C、函数的图象关于点中心对称 D、函数在区间内单调递增
-
19、已知是定义在上连续可导函数,其导函数为 , 若 , 且 , 则不等式的解集为( )A、 B、 C、 D、
-
20、若P是△ABC所在平面内一点,则“”是“△ABC为直角三角形”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件