相关试卷
-
1、已知 , 分别是双曲线:( , )的左、右焦点,为双曲线右支上一点,的最小值为1,且当轴时, , 则( )A、双曲线的焦距为4 B、双曲线的一条渐近线被圆:截得的弦长为2 C、过点作双曲线的一条渐近线的垂线,垂足为 , 则 D、为圆:上一点,的最大值为3
-
2、设函数 , 则下列说法正确的是( )A、的最大值为 B、在上单调递增 C、 , 在上存在极值点 D、的图象向右平移个单位长度后得到的图象对应的函数为偶函数
-
3、已知 , , , 是球的球面上四点, , , , . 记球的体积为 , 四面体的体积为 , 则的值为( )A、 B、 C、 D、
-
4、已知函数满足 , , 则( )A、3 B、 C、5 D、
-
5、已知不共线的向量 , 满足 , , , 则的最小值为( )A、 B、2 C、 D、
-
6、已知函数图象上不同的两点 , 到直线的距离相等,则( )A、 B、 C、 D、
-
7、已知 , , 则( )A、2 B、1 C、 D、
-
8、已知为正项等比数列的前项和, , , 则( )A、2 B、3 C、4 D、6
-
9、若复数满足 , 则在复平面内,对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
10、已知集合 , , 则( )A、 B、 C、 D、
-
11、二次函数的图象是抛物线, 现在我们用 “图象平移” 的方式讨论其焦点与准线, 举例如下: 二次函数的图象可以由的图象沿向量平移得到; 抛物线 , 即的焦点坐标为 , 准线方程为 ; 故二次函数的焦点坐标为 , 准线方程为 .(1)、求二次函数的焦点坐标和准线方程;(2)、求二次函数的焦点坐标和准线方程;(3)、设过的直线与抛物线的另一个交点为 , 直线与直线交于点 , 过点作轴的垂线交抛物线于点. 是否存在定点 , 使得三点共线? 若存在,请求出定点的坐标; 若不存在,请说明理由.
-
12、已知函数.(1)、当时,求曲线在处的切线方程;(2)、若有两个不同的零点 , .
(ⅰ)求实数的取值范围;
(ⅱ)证明:.
-
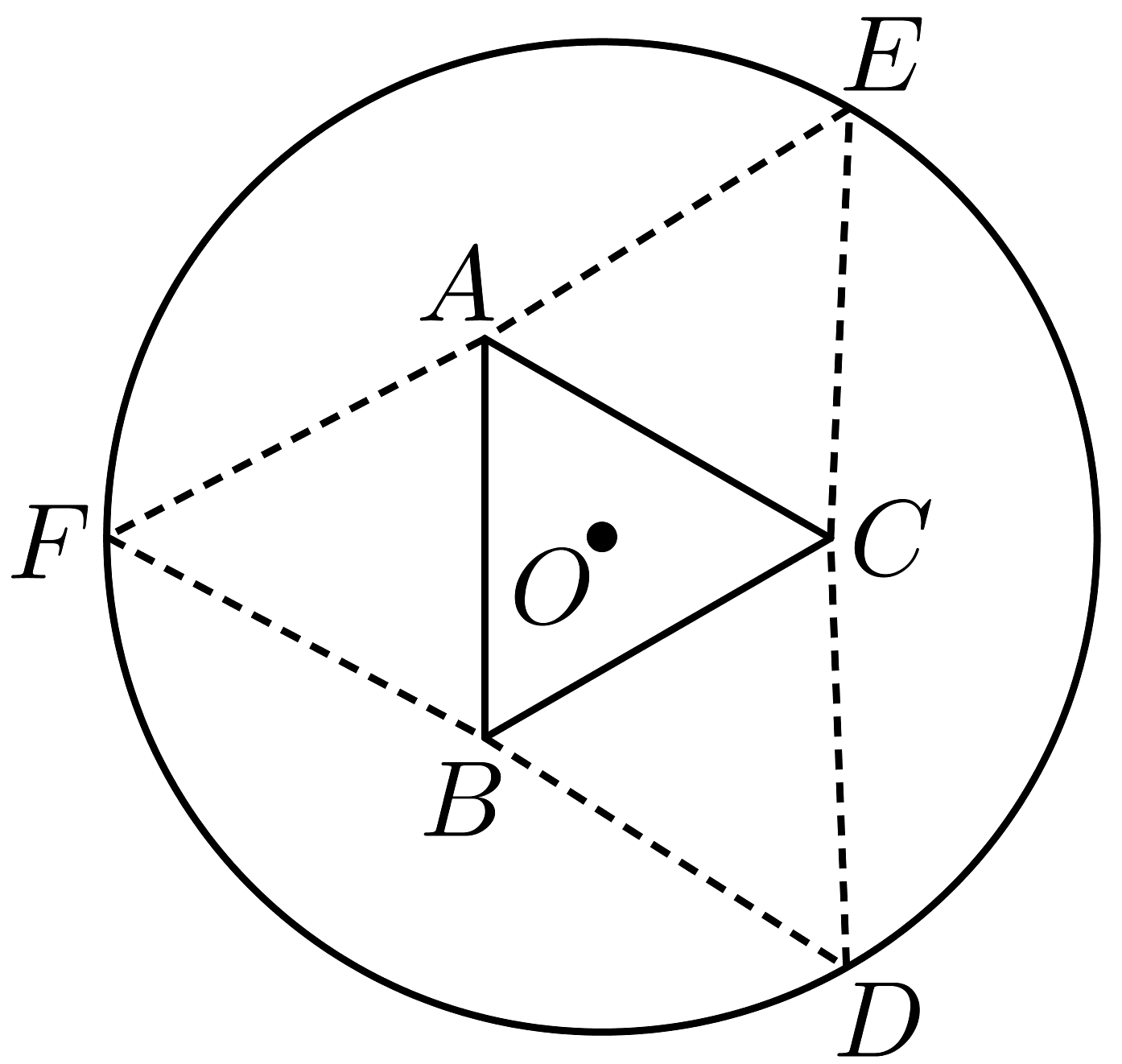
13、如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为 .
-
14、等比数列的前n项和为 , 若 , 且与的等差中项为 , 则.
-
15、“杨辉三角”是二项式系数在三角形中的一种几何排列,在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中就有出现.在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数之和,例如第4行的6为第3行中两个3的和,则下列命题中正确的是( )
 A、在“杨辉三角”中,第行的所有的数字之和为 B、在“杨辉三角”第行的数中,从左到右第个数最大 C、在“杨辉三角”中,从第3行开始,取每行的第4个数得到一数列,则该数列前10项之和为 D、记“杨辉三角”第行的第个数为 , 则的值恰好是第行的中间一项的数字
A、在“杨辉三角”中,第行的所有的数字之和为 B、在“杨辉三角”第行的数中,从左到右第个数最大 C、在“杨辉三角”中,从第3行开始,取每行的第4个数得到一数列,则该数列前10项之和为 D、记“杨辉三角”第行的第个数为 , 则的值恰好是第行的中间一项的数字 -
16、已知函数 , 则( )A、的图象关于点对称 B、的最小正周期为 C、的最小值为 D、在上有四个不同的实数解
-
17、为了解目前本市高二学生身体素质状况,对某校高二学生进行了体能抽测,得到学生的体育成绩 , 其中60分及以上为及格,90分及以上为优秀,则下列说法正确的是( )
参考数据:随机变量 , 则 , , .
A、该校学生体育成绩的方差为100 B、该校学生体育成绩的期望为70 C、该校学生体育成绩不及格的人数和优秀的人数相当 D、该校学生体有成绩的及格率不到 -
18、若函数在上单调递增,则的取值范围为( )A、 B、 C、 D、
-
19、定义:若函数与在公共定义域内存在 , 使得 , 则称与为“契合函数”,为“契合点”.(1)、若与为“契合函数”,且只有一个“契合点”,求实数a的取值范围.(2)、若与为“契合函数”,且有两个不同的“契合点” .
①求b的取值范围;
②证明: .
-
20、给定一个数列 , 记 , 则把数列称为的一阶差数列.若数列的一阶差数列的通项公式为 , 则( )A、556 B、557 C、292 D、291