相关试卷
-
1、如图四棱锥中,底面为菱形且 , 侧面是边长为2的正三角形,且侧面底面 , M为的中点.
 (1)、求与底面所成的角的大小;(2)、求证:平面平面;(3)、求平面和平面的夹角的余弦值.
(1)、求与底面所成的角的大小;(2)、求证:平面平面;(3)、求平面和平面的夹角的余弦值. -
2、在中,角所对的边长组成公差为1的等差数列.(1)、若 , 求的周长和面积;(2)、为锐角三角形,求整数的最小值.
-
3、2025年4月24日,搭载“神舟二十号”的火箭发射升空,有很多民众通过手机、电视等方式观看有关新闻.某机构将关注这件事的时间在2小时以上的人称为“航天爱好者”,否则称为“非航天爱好者”,该机构通过调查,从参与调查的人群中随机抽取200人进行分析,得到下表(单位:人):
航天爱好者
非航天爱好者
合计
女
40
60
100
男
70
30
100
合计
110
90
200
(1)、能否有99%的把握认为“航天爱好者”或“非航天爱好者”与性别有关?(2)、现从这100名男生与100名女生中,按“航天爱好者”和“非航天爱好者”这两种类型分别进行分层抽样抽取男生10人,女生5人.将这15人中航天爱好者记为A组,非航天爱好者记为B组.现从这两组中各任意选取一人进行交换,求经过一次交换后,A组中女生人数的分布列和数学期望.附: , 其中 ,
0.10
0.05
0.010
0.005
0.001
2.706
3.841
6.635
7.879
10.828
-
4、函数的最小值为 .
-
5、要安排4名学生到3个乡村做志愿者,每名学生只能选择去一个村,每个村里至少有一名志愿者,则不同的安排方法共有种.
-
6、直线被圆截得的弦长为.
-
7、斜率为的直线过抛物线的焦点 , 且与抛物线交于M、N两点,为抛物线的准线上任意一点.则( )A、 B、以为直径的圆与直线相切 C、为等边三角形,则 D、为抛物线的切线,则
-
8、如图1,在中, , , , 、分别在AB,AC上,且.将沿翻折得到图2,其中.记三棱锥外接球球心为 , 球表面积为 , 三棱锥外接球球心为 , 球表面积为 , 则在图2中,下列说法正确的有( )
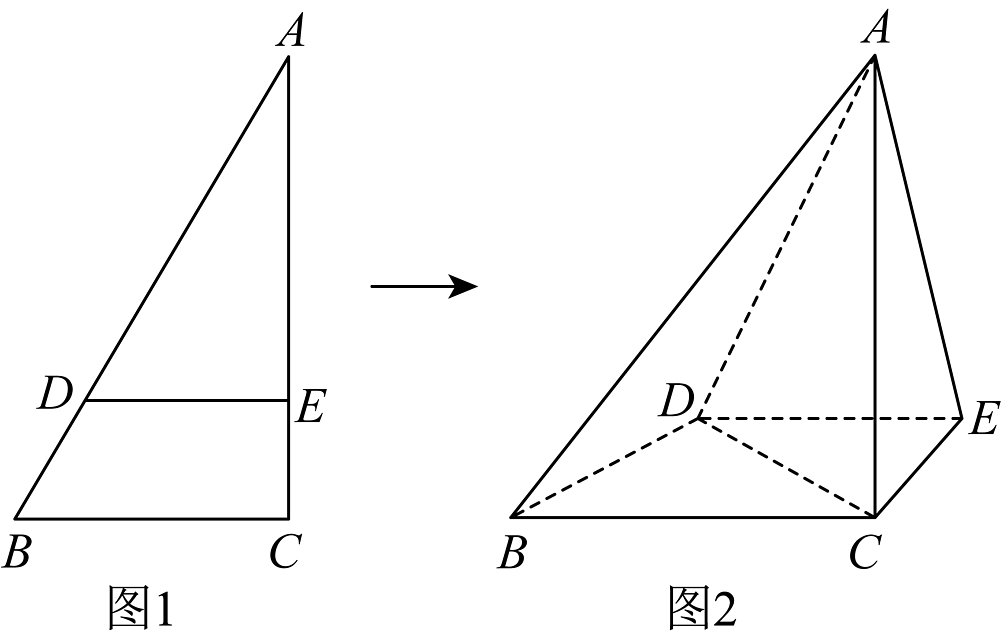 A、 B、直线与所成角的正弦值为 C、平面 D、
A、 B、直线与所成角的正弦值为 C、平面 D、 -
9、函数 , 若在有最大值,则实数的取值范围是( )A、 B、 C、 D、
-
10、已知函数的部分图象如图所示,下列说法正确的是( )
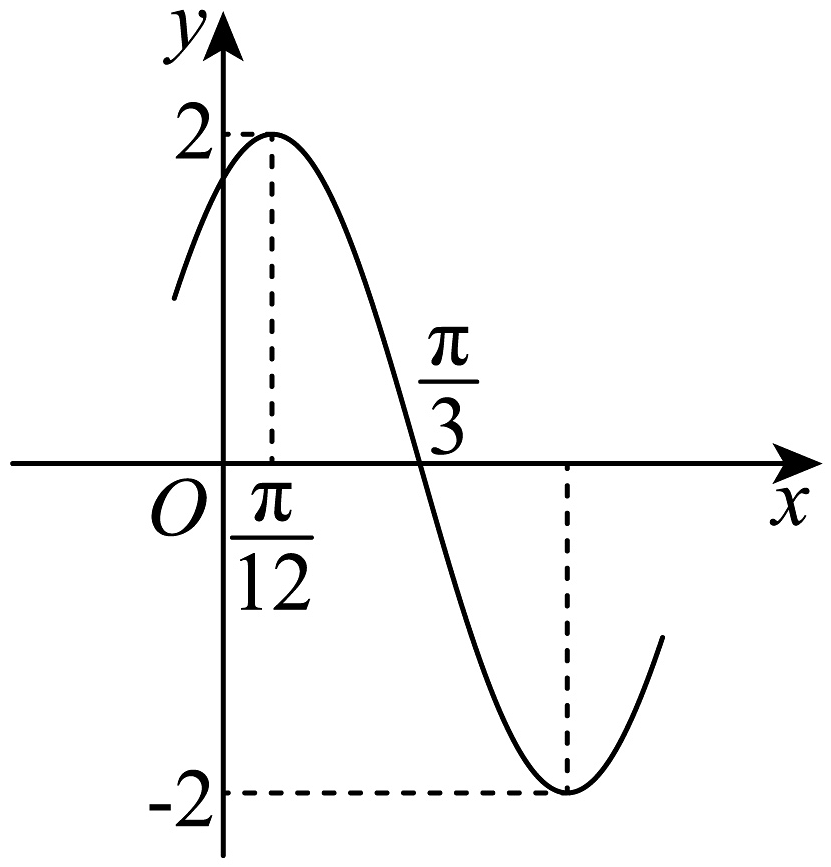 A、函数的图象关于直线对称 B、函数的图象关于点对称 C、函数在上单调递减 D、当时,
A、函数的图象关于直线对称 B、函数的图象关于点对称 C、函数在上单调递减 D、当时, -
11、已知 , , 则( )A、 B、 C、 D、
-
12、命题:数列为等比数列,命题:数列满足 , , , 则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
13、双曲线的离心率为 , 则该双曲线的焦点到它的渐近线距离为( )A、1 B、2 C、 D、3
-
14、在中,是边上的中点,则( )A、 B、 C、 D、
-
15、已知集合 , , 则( )A、 B、 C、 D、
-
16、已知 , 则( )A、3 B、5 C、 D、
-
17、空气中的尘埃,天上的云朵飘忽随机不定、这些动态随机现象的研究有着重要的意义.在平面直角坐标系中,粒子从原点出发,等可能向四个方向移动,即粒子每秒向左、向右、向上或向下移动一个单位,如在1秒末,粒子会等可能地出现在 , , , 四点处.(1)、求粒子在第2秒末移动到点的概率;(2)、记第秒末粒子回到原点的概率为.
(i)已知求以及;
(ii)令 , 记为数列的前项和,若对任意实数 , 存在 , 使得 , 则称粒子是常返的.已知证明:该粒子是常返的.
-
18、已知椭圆的离心率为 , 且.
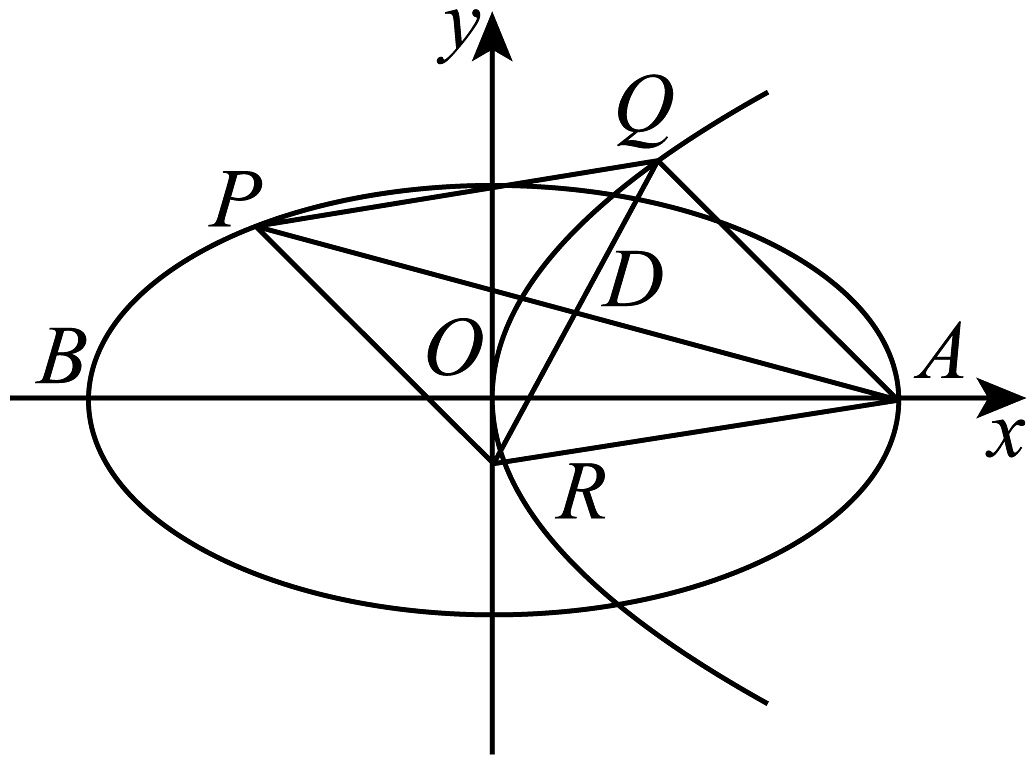 (1)、求椭圆的方程;(2)、已知B,A是椭圆的左、右顶点,不与轴平行或重合的直线交椭圆于M,N两点,记直线的斜率为 , 直线的斜率为 , 且 , 证明:直线过定点;(3)、如图,点为椭圆上不同于A,B的任一点,在抛物线上存在两点R,Q,使得四边形为平行四边形,求的最小值.
(1)、求椭圆的方程;(2)、已知B,A是椭圆的左、右顶点,不与轴平行或重合的直线交椭圆于M,N两点,记直线的斜率为 , 直线的斜率为 , 且 , 证明:直线过定点;(3)、如图,点为椭圆上不同于A,B的任一点,在抛物线上存在两点R,Q,使得四边形为平行四边形,求的最小值. -
19、已知函数 , .(1)、若曲线在点处的切线斜率为4,求的值;(2)、当时,讨论函数的单调性;(3)、已知的导函数在上存在零点,求证:当时,.
-
20、如图,已知正方形和等腰梯形所在的平面互相垂直, , , .
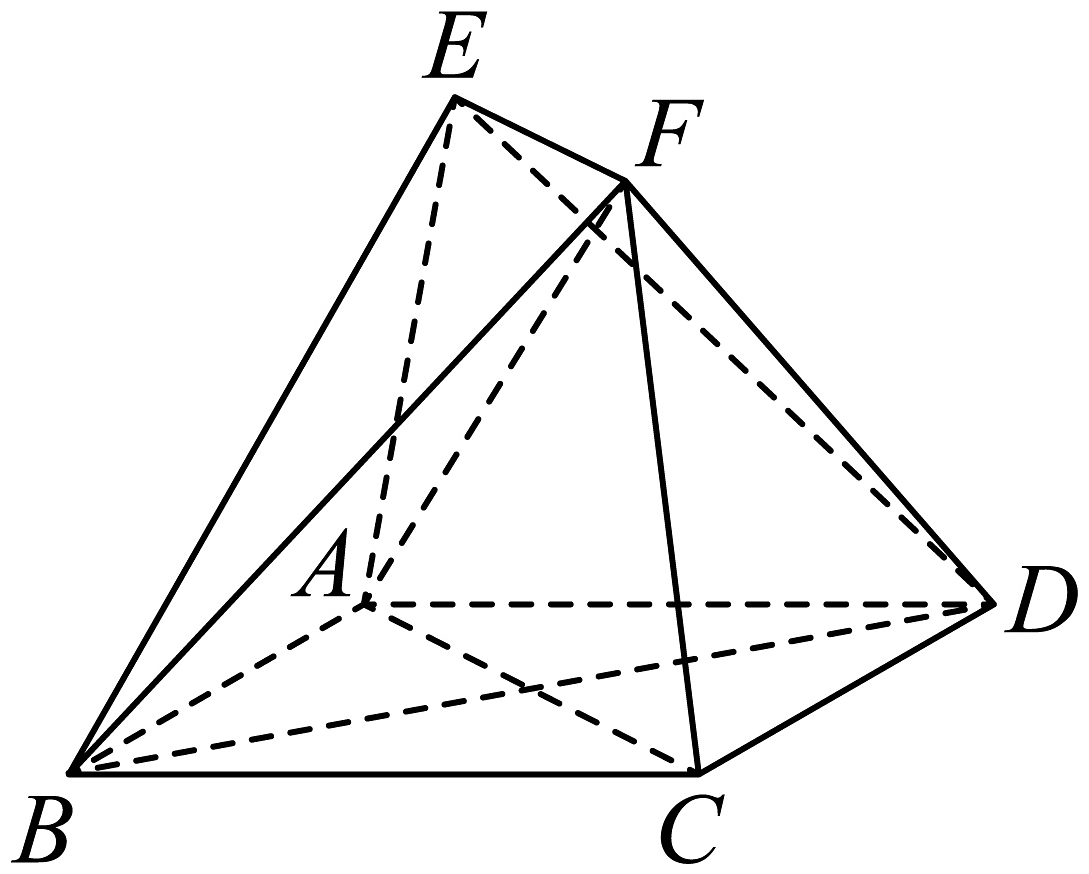 (1)、求证:平面;(2)、若 , 求二面角的正弦值.
(1)、求证:平面;(2)、若 , 求二面角的正弦值.