相关试卷
-
1、已知向量 , , .(1)、求;(2)、求与的夹角.
-
2、已知向量 , , 则在上的投影向量的坐标是.
-
3、如图,在正方体中,点P在线段上运动,则下列结论正确的是( )
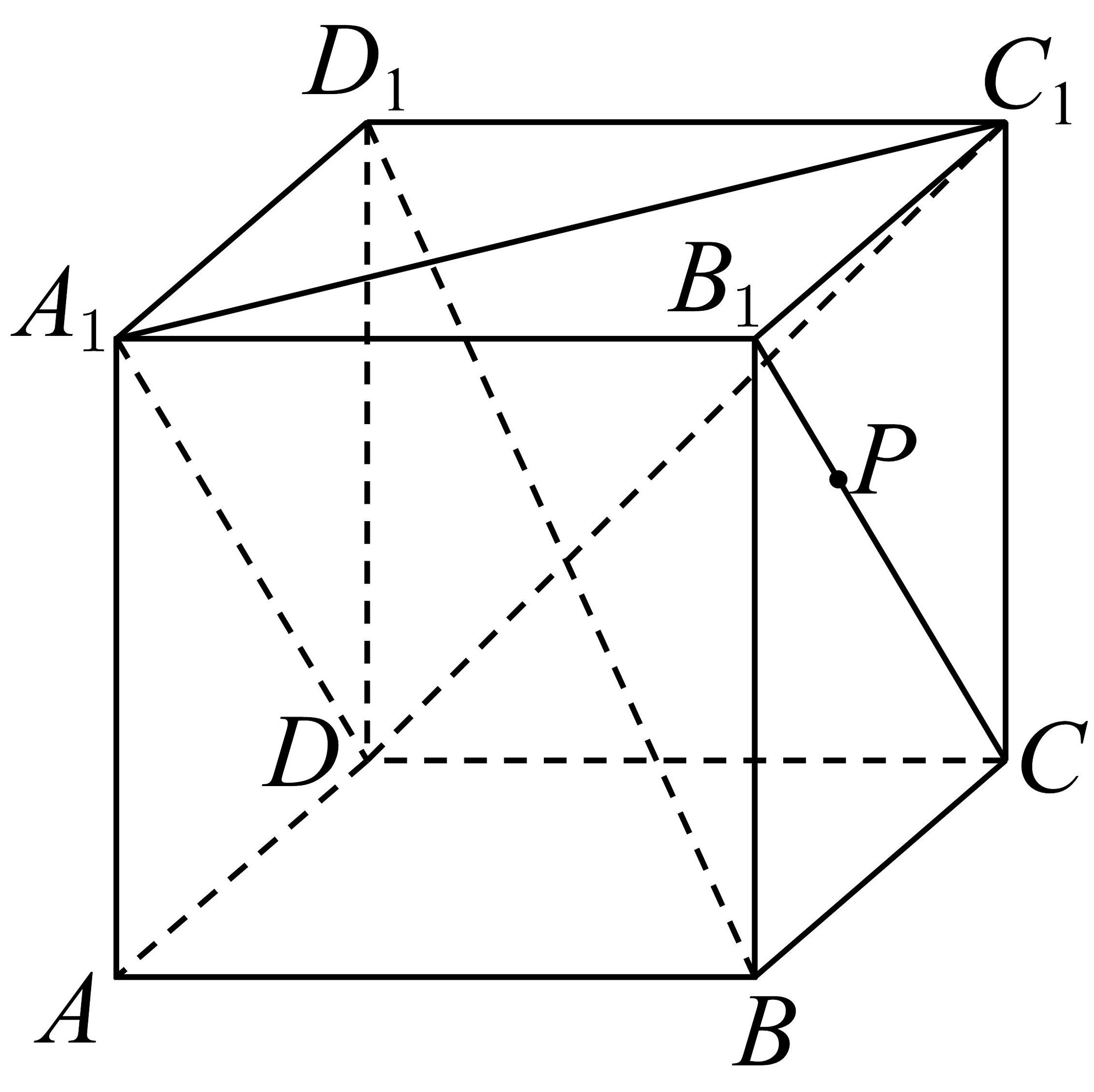 A、直线平面 B、三棱锥的体积为定值 C、异面直线与所成角的取值范围是 D、当P为的中点时,直线与平面所成角的正弦值为
A、直线平面 B、三棱锥的体积为定值 C、异面直线与所成角的取值范围是 D、当P为的中点时,直线与平面所成角的正弦值为 -
4、已知是定义在上的偶函数,且是奇函数,当时, , 则( )A、的值域为 B、的最小正周期为4 C、在上有3个零点 D、
-
5、下列选项中,值为的是( )A、 B、 C、 D、
-
6、在中,点在边上,且满足 , 点为线段上任意一点(除端点外),若实数 , 满足 , 则的最小值为( )A、 B、 C、 D、9
-
7、设函数是奇函数.若函数 , 则( )A、28 B、33 C、38 D、43
-
8、若 , 且 , 则的值为A、 B、 C、 D、
-
9、已知平面向量 , , 则“或”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件
-
10、已知是第二象限的角,为其终边上的一点,且 , 则( )A、-6 B、 C、 D、
-
11、复数的虚部为( )A、 B、1 C、 D、i
-
12、已知命题 , 则是( ).A、 B、 C、 D、
-
13、已知集合 , 则 ( )A、 B、 C、 D、
-
14、已知函数 .(1)、当时,判断函数的奇偶性,并说明理由;(2)、利用三角恒等变换,分别求函数在 , 4,6时的取值范围;(3)、请结合(2)的结果猜想函数的取值范围,然后证明你的猜想,并求方程有解时n的最小值.
-
15、下列函数在其定义域上既是奇函数又是增函数的是( )A、 B、 C、 D、
-
16、点A是曲线上任意一点,则点A到直线的最小距离为( )A、 B、 C、 D、
-
17、已知函数 , 若过点的两条互相垂直的直线分别与的图象交于另外的点和 , 且四边形ABCD为正方形,则这两条直线的斜率之和为 .
-
18、若命题 , 命题直线与抛物线无公共点,则是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
19、如图,四棱锥中,底面 , , , , 平面PAD与平面PBC的交线为l,且 .
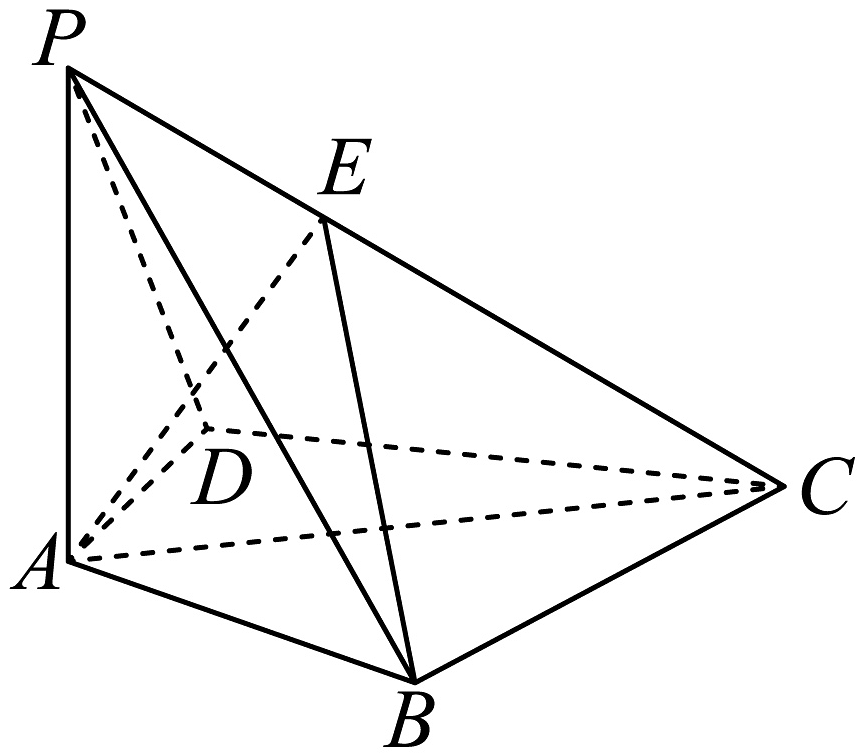 (1)、证明;(2)、若 , 求平面ABE与平面PCB夹角的余弦值.
(1)、证明;(2)、若 , 求平面ABE与平面PCB夹角的余弦值. -
20、如图,在直三棱柱中, , , 点M是线段上一点,则下列说法正确的是( )
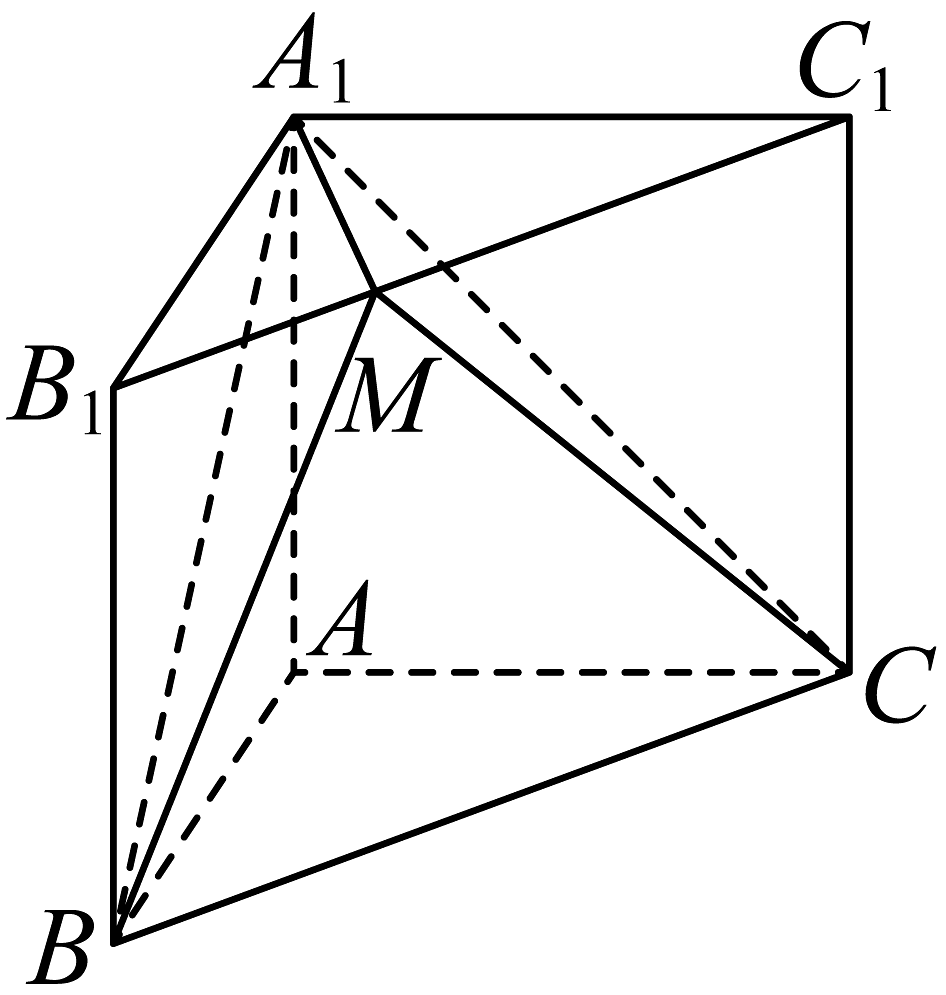 A、当M为的中点时,平面 B、四面体的体积为定值 C、的最小值为 D、四面体的外接球半径的取值范围是
A、当M为的中点时,平面 B、四面体的体积为定值 C、的最小值为 D、四面体的外接球半径的取值范围是