相关试卷
-
1、如图,四棱锥底面是边长为4的正方形,若点M在四边形内(包含边界)运动,N为的中点, , , 则( ).
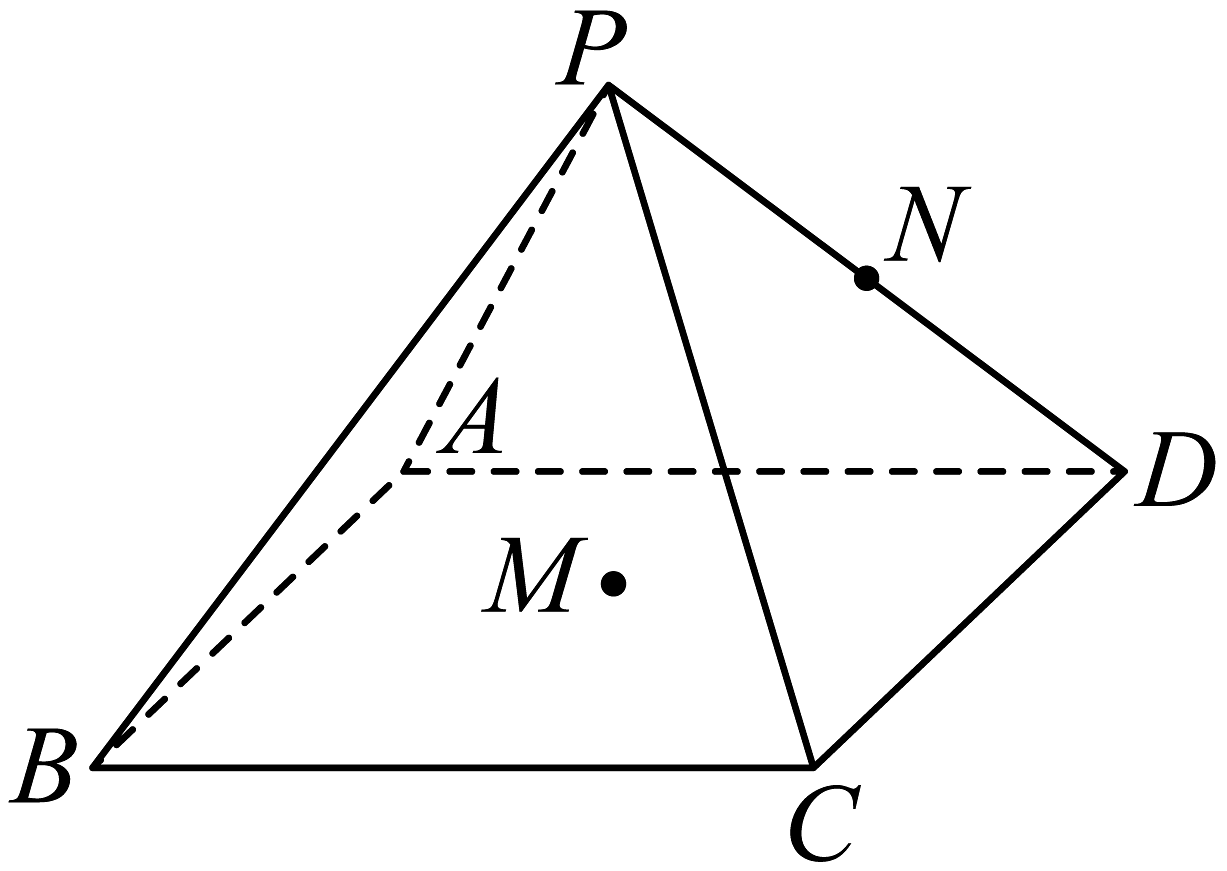 A、当M为的中点时,异面直线与所成角为 B、当平面时,点M的轨迹长度为 C、当与平面所成的角是时,点M到的距离可能为 D、点Q是四棱锥外接球上的一点,则的最大值是
A、当M为的中点时,异面直线与所成角为 B、当平面时,点M的轨迹长度为 C、当与平面所成的角是时,点M到的距离可能为 D、点Q是四棱锥外接球上的一点,则的最大值是 -
2、已知复数 , 则( ).A、 B、 C、 D、是方程的根
-
3、已知正实数a,b满足 , 则( ).A、 B、 C、 D、
-
4、设抛物线的焦点为F,过抛物线上点P作其准线的垂线,设垂足为Q,若 , 则( ).A、 B、 C、 D、
-
5、已知直线与圆相交于M、N两点,则的最大值为( ).A、 B、 C、4 D、
-
6、设直线与平面相交但是不垂直,则下列说法中正确的是( )A、平面内的直线与直线都不垂直 B、过直线的平面与平面都不垂直 C、与直线垂直的直线可能与平面垂直 D、与直线平行的平面可能与平面垂直
-
7、 , 则的值为( ).A、 B、 C、 D、
-
8、已知等差数列的前n项和为 , 并且满足 , , 则为( ).A、17 B、15 C、11 D、9
-
9、已知集合 , , 则“”是“”的( ).A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
10、已知向量 , , 若 , 则( )A、 B、2 C、 D、0
-
11、已知函数为奇函数,其函数图象经过点.(1)、求 , 的值;(2)、证明:函数在区间上单调递增;(3)、若命题:“ , ”为真命题,求实数的取值范围.
-
12、已知________.请从下列两个条件中任选一个作答.
条件①:角的终边与单位圆的交点为;
条件②:角满足.
(1)、求的值;(2)、求的值.注:如果多个条件分别作答,按第一个解答计分.
-
13、已知集合 , .(1)、求;(2)、若 , 为集合,定义集合运算 , 求 .
-
14、已知函数在定义域上单调递增, , , , 则函数的一个误差不超过0.05的零点可以为( )A、0.6 B、0.68 C、0.7 D、0.72
-
15、设 , 则( )A、 B、 C、 D、
-
16、已知直线: , 直线: , 则“”是“”的( )条件.A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要
-
17、对于函数 , 若在定义域内存在实数 , 满足 , 则称为“局部反比例对称函数”.(1)、已知函数 , 试判断是不是“局部反比例对称函数”.并说明理由;(2)、用定义证明函数在为单调递增函数;(3)、若是定义在区间上的“局部反比例对称函数”,求实数的取值范围.
-
18、在中,角 , , 所对的边分别为 , , , 满足 .(1)、求角 .(2)、为边上一点,且 .
①若 , 求当取最小值时的值;
②若为角平分线,求的取值范围.
-
19、如图,在四棱锥中,底面是菱形, , 且 , 侧棱底面 , , 为中点.
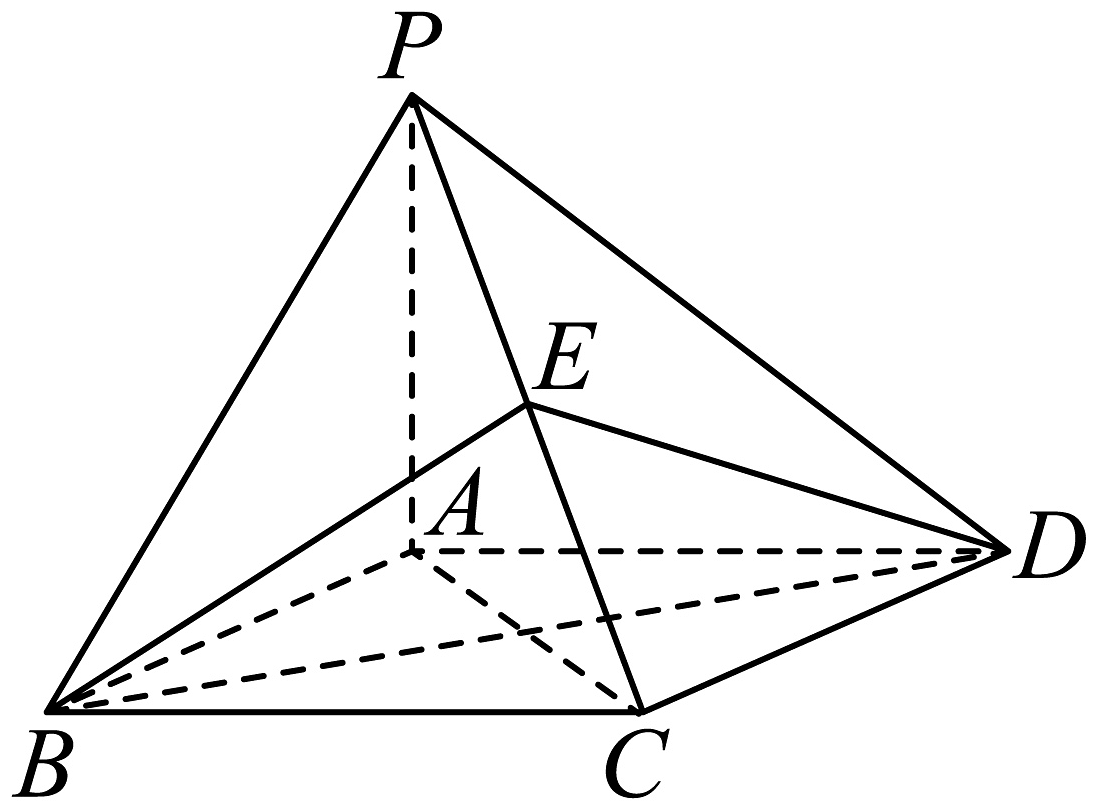 (1)、证明:平面;(2)、求三棱锥的体积;(3)、求二面角的平面角的大小.
(1)、证明:平面;(2)、求三棱锥的体积;(3)、求二面角的平面角的大小. -
20、已知函数的部分图像如图所示.
 (1)、求函数的解析式,并求它的对称中心的坐标;(2)、将函数的图像向右平移个单位,得到函数的图像,为偶函数,求函数的单调递减区间.
(1)、求函数的解析式,并求它的对称中心的坐标;(2)、将函数的图像向右平移个单位,得到函数的图像,为偶函数,求函数的单调递减区间.