相关试卷
-
1、若m,n为两条直线,α为一个平面,则下列结论中正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则m与n相交
-
2、已知函数 , 曲线在处的切线也与曲线相切.(1)、求实数的值;(2)、若是的最大的极小值点,是的最大的极大值点,求证:.
-
3、若函数对于一切恒成立,则求实数的取值范围.
-
4、已知数列的前n项和为 , 且 , .
(1)求的通项公式 ;
(2)设若 , 恒成立,求实数的取值范围.
-
5、如图,在四棱锥中,底面满足 , , 底面 , 且 , .
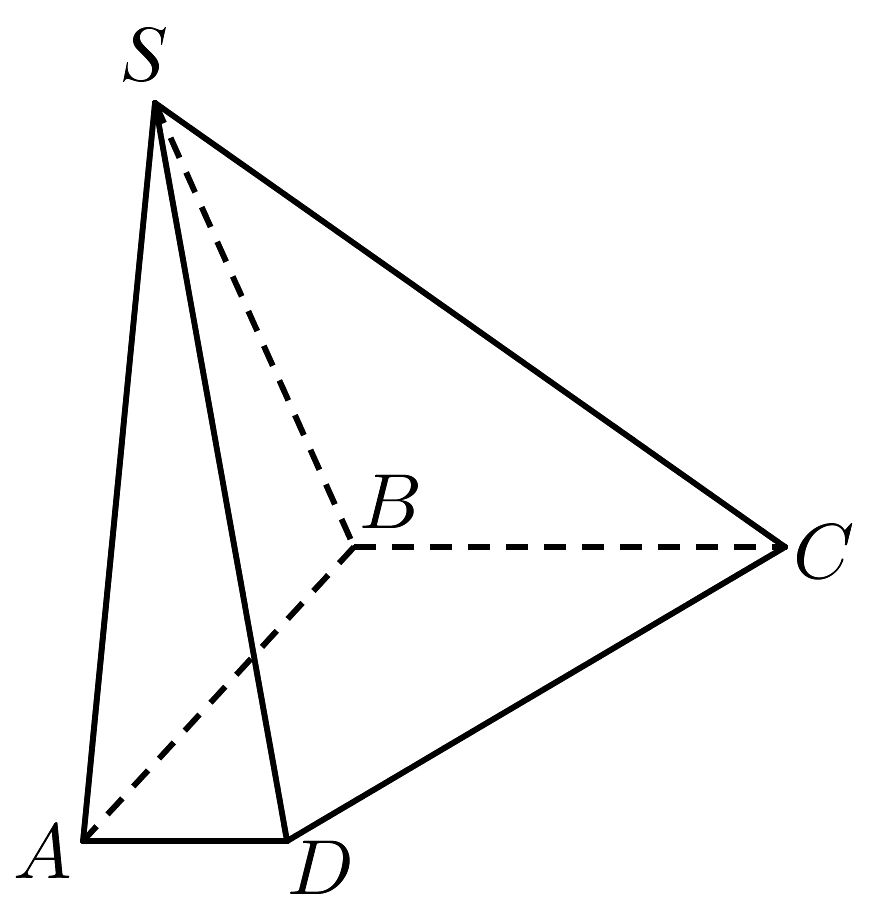 (1)、证明平面;(2)、求平面与平面的夹角.
(1)、证明平面;(2)、求平面与平面的夹角. -
6、在中,角 , , 所对的边分别为 , 已知 .
(1)求角 的大小;
(2)若 , 求的面积.
-
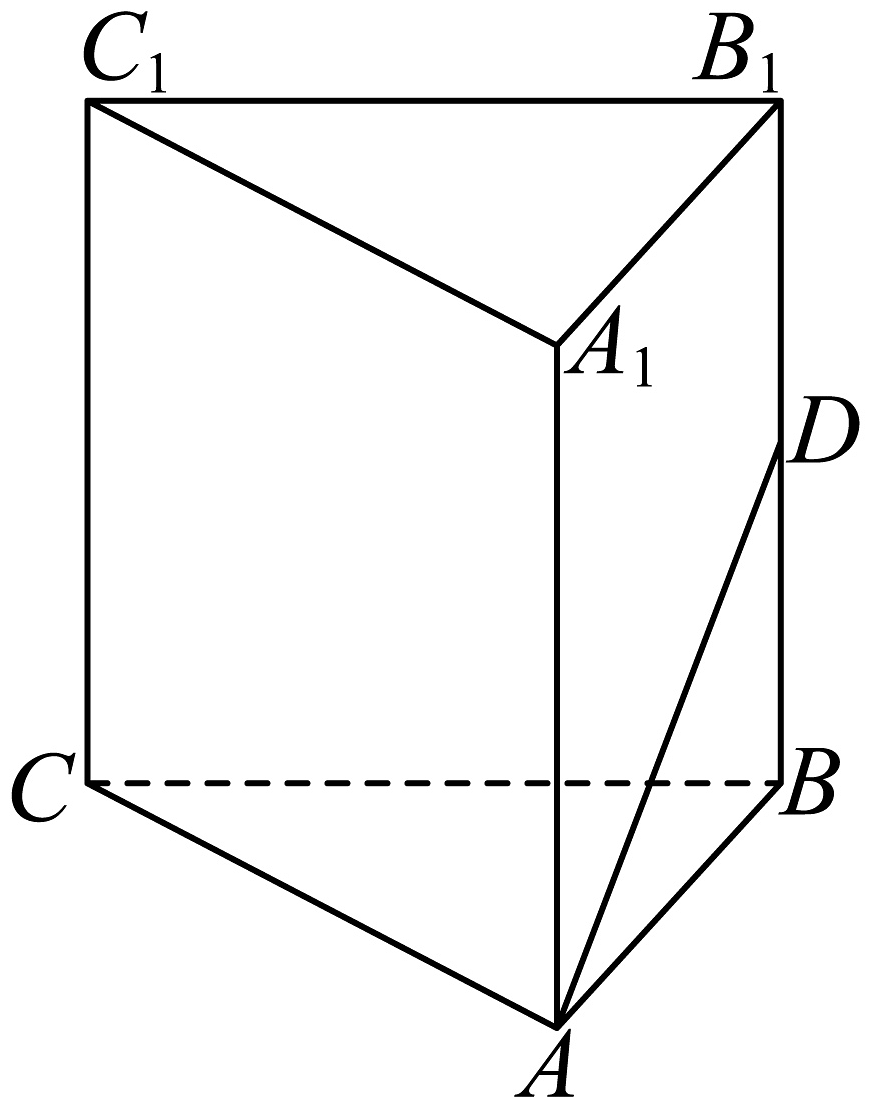
7、如图,在正三棱柱中,已知在棱上,且 , 若与平面所成的角为 , 则为.
-
8、名男生和名女生排成一排,若女生必须相邻,则有种不同排法.用数字作答
-
9、若函数是偶函数,是奇函数,已知存在点 , , 使函数在、点处的切线斜率互为倒数,那么.
-
10、若角的终边经过点 , 则下列结论正确的是( )A、是钝角 B、是第二象限角 C、 D、点在第四象限
-
11、已知定义在R上的函数满足 . 且 , 若 , 则下面说法正确的是( )A、函数的图像关于对称 B、 C、函数在上单调递增 D、若函数的最大值与最小值之和为2,则
-
12、在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各项中,一定符合上述指标的是( )A、平均数 B、标准差 C、平均数且极差小于或等于 D、众数等于且极差小于或等于
-
13、下列函数中,既是奇函数又在单调递增的是( )A、 B、 C、 D、
-
14、已知函数 , 则函数的最大值和周期分别是( )A、 , B、 , C、2, D、2,
-
15、已知集合 , , 则( )A、 B、 C、 D、
-
16、《几何原本》里提出:“球的体积()与它的直径()的立方成正比”,即 , 其中常数称为“立圆率”.对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式求体积(在等边圆柱中,表示底面圆的直径;在正方体中,表示棱长),设运用此体积公式求得等边圆柱(底面圆的直径为)、正方体(棱长为)、球(直径为)的“立圆率”分别为、、 , 则( )A、 B、 C、 D、
-
17、如图,在平行四边形中,( )
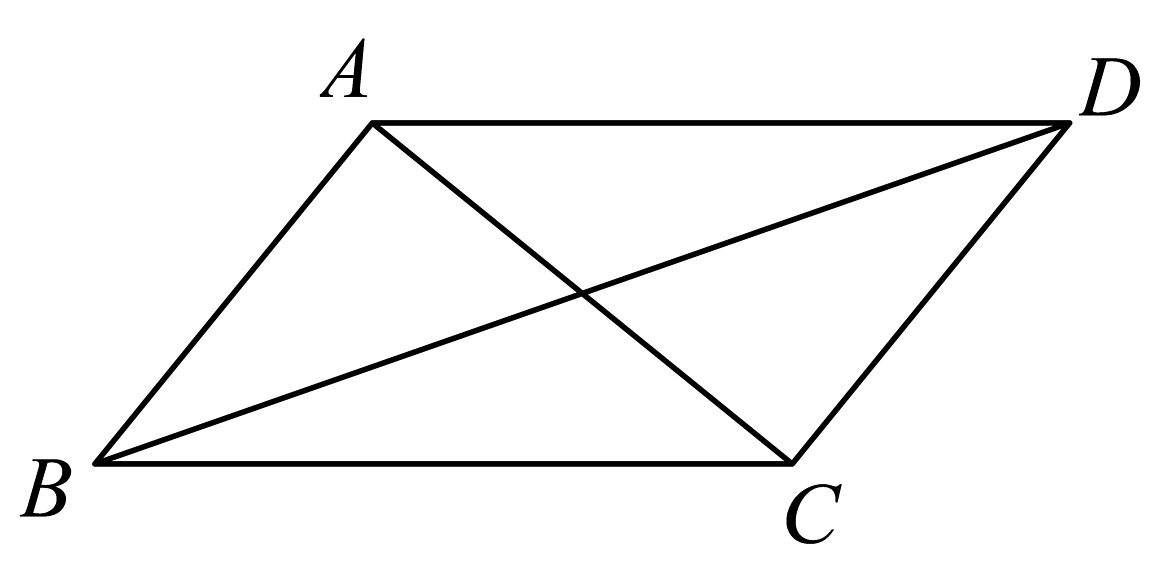 A、 B、 C、 D、
A、 B、 C、 D、 -
18、复数( )A、 B、 C、 D、
-
19、函数(1)、求的单调区间;(2)、设 , 证明:;(3)、若 , , 比较与2的大小,并说明理由.
-
20、平面直角坐标系中,点 , 动点满足以为直径的圆与圆内切,记点的轨迹为曲线.(1)、求曲线的方程;(2)、是曲线上的任意一点,过斜率存在的直线交曲线于两不同点A、B,射线交曲线于点.
(ⅰ)证明:为定值;
(ⅱ)求面积的取值范围.